AI思想启蒙

【AI思想启蒙13】深度学习第3篇-度量学习

度量学习通过孪生网络学习嵌入空间，使语义相似的样本距离近、不相似样本距离远。核心是对比损失拉近正样本、推远负样本（带margin）。训练需成对标签，推理仅算距离，支持人脸验证、推荐召回等任务。

Posted by Hilda on November 24, 2025

度量学习

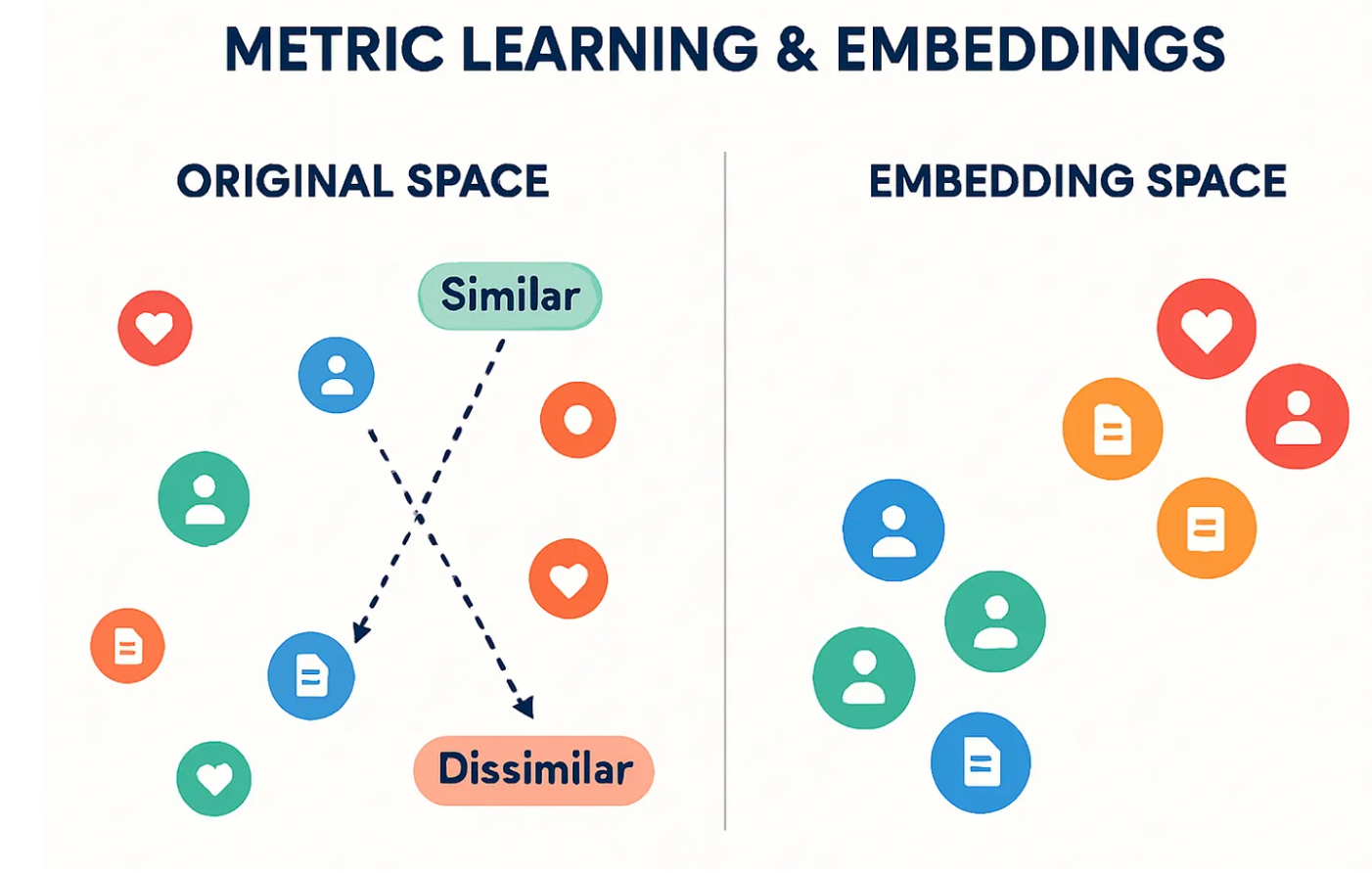
image-20251124140910980

在许多人工智能应用（如人脸识别、推荐系统和搜索引擎）中，关键的挑战是测量数据点之间的相似性。因此诞生了度量学习和嵌入向量。

度量学习的核心在于学习一种映射，将原始、复杂的输入数据转换到一个新的、低维的特征空间，在这个空间中，距离可以直接反映语义上的相似性。

通过神经网络或其他表示方法，将输入数据 \(x\) 映射到一个特征空间（Feature Space），即嵌入（Embedding）。这个神经网络（孪生网络或三元组网络）充当了一个编码器，将高维数据（如图像的数百万像素或文本的词汇表）压缩成一个短而稠密的向量。

定义一个损失函数（Loss Function），鼓励相似的点靠得近，不相似的点离得远。这是度量学习的驱动力。与分类任务不同，损失函数不惩罚错误分类，而是惩罚不正确的相对距离。它确保了在学习到的嵌入空间中，几何距离（如欧氏距离）与数据的语义相似度一致。

传统的距离（如原始像素上的欧氏距离）对噪声敏感。度量学习则让神经网络根据任务数据，自主地调整特征提取，使最终的嵌入空间中的距离真正符合人类的语义判断。

注意：相似/不相似（即我们用于训练的标签 \(Y\)）对于模型来说是已知的输入。

在度量学习的训练阶段，这些信息被称为监督信息（Supervision）或真实标签（Ground Truth），它是用来指导模型学习的。

在训练度量学习模型时，我们需要构建特殊的训练样本，通常是：

  • 相似对（Positive Pair）： 一对来自同一类别或具有相同语义的样本 \((X_i, X_j)\)，其标签 \(Y=1\)。
  • 不相似对（Negative Pair）： 一对来自不同类别或不相似语义的样本 \((X_i, X_k)\)，其标签 \(Y=0\)。

在训练时，模型接收的输入是：

\[(X_i, X_j, Y)\]

度量学习核心目标是学习一个有效的距离函数或相似性度量。这个度量函数能够使得在原始输入空间中相似的样本在新的特征空间中距离接近，而不相似的样本距离较远。度量学习不是学习分类边界，而是学习一个能够将语义相似性转化为空间距离的特征映射函数。模型的工作就是找到一个特征映射函数，使得这种已知关系在嵌入空间中得到最好的体现。

如果两个输入需要通过拥有相同权重的模型进行处理，则模型共享参数。

度量学习的本质是比较成对的（pair）或三元的（triplet）输入样本之间的关系，它不再只关注单个样本的分类结果。

最终目标是学习一个嵌入空间（Embedding Space），在这个空间中，距离能够直接反映语义上的相似度。例如，“可爱的宝宝”和“惹人喜欢的孩子”这两个语义相似的输入，在嵌入空间中应该非常接近。

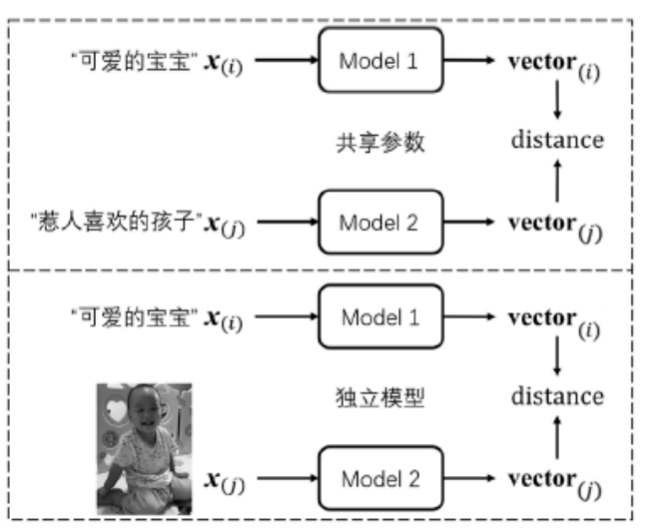
image-20251124110902616

度量学习通常使用孪生网络（Siamese Network）或类似结构来实现，主要区别在于模型是否共享权重。

3.1损失函数-对比损失

对比损失(Contrastive Loss)是孪生网络中最常用的损失函数之一。对比损失要求：1) 相似的样本对之间的距离最小化；2) 不相似的样本对之间的距离必须大于一个预设的边际值（Margin）。

  • 如果输入的两个样本相似 (\(\text{label} = 1\))，则最小化它们的嵌入距离 \(D\)。
  • 如果输入的两个样本不相似 (\(\text{label} = 0\))，则最大化它们的嵌入距离，但只到边际值 \(m\) (margin) 为止。
\[\mathcal{L}(Y, D) = \frac{1}{2} Y D^2 + \frac{1}{2} (1-Y) \max(0, m - D)^2\]

其中：

  • \(Y\): 标签，1 表示相似，0 表示不相似。
  • \(D\): 两个嵌入向量之间的欧氏距离（Euclidean Distance） $$D =   \text{vector}{(i)} - \text{vector}{(j)}   _2$$。
  • \(m\): 边际值 (Margin)，一个大于 0 的常量。

或者表述成：\(\text{Loss} = \underbrace{\sum_{y_{(i,j)}=1} D_{(i,j)}}_{\text{相似对的惩罚项}} + \underbrace{\sum_{y_{(i,k)}=0} \text{hingle}(m-D_{(i,k)})}_{\text{不相似对的惩罚项}}\)

其中：

  • \(y_{(i,j)}\)：样本 \(\text{vector}_{(i)}\) 和 \(\text{vector}_{(j)}\) 之间的标签。
    • \(y=1\) 表示 \(\text{vector}_{(i)}\) 和 \(\text{vector}_{(j)}\) 属于相似对（Positive Pair）。
    • \(y=0\) 表示 \(\text{vector}_{(i)}\) 和 \(\text{vector}_{(k)}\) 属于不相似对（Negative Pair）。
  • \(D_{(i,j)}\)：两个嵌入向量之间的距离。当 \(\text{vector}_{(i)}\) 和 \(\text{vector}_{(j)}\) 相似时（\(y=1\)），损失函数直接惩罚它们的距离 \(D_{(i,j)}\)。模型优化的方向是不断减小 \(D_{(i,j)}\)，将相似样本的嵌入点在空间中拉近。
  • \(m\)：边际值（Margin），一个预设的超参数，决定了不相似样本应至少保持的距离。
  • \(\text{hingle}(\cdot)\)：通常指 \(\max(0, \cdot)\) 函数，类似于支持向量机（SVM）中的 Hinge Loss。

欧式距离：\(D_{A,B} = \|\text{vector}_A - \text{vector}_B\|_2 = \sqrt{\sum_{i=1}^{k} (\text{vector}_{A,i} - \text{vector}_{B,i})^2}\)，其中 \(k\) 是嵌入向量的维度。

余弦距离 (Cosine Distance):如果训练时使用的是余弦相似度相关的损失，那么我们通常会计算余弦距离。它衡量的是两个向量方向的差异，与向量的长度无关：

\[\text{Similarity}_{A,B} = \frac{\text{vector}_A \cdot \text{vector}_B}{\|\text{vector}_A\|_2 \|\text{vector}_B\|_2}\] \[\text{Distance}_{A,B} = 1 - \text{Similarity}_{A,B}\]

注意点：

【1】相似/不相似（即标签 \(y\)）是训练时的已知信息，但模型最终要求得的是这个关系在嵌入空间中的表达（距离）。在训练度量学习模型时，我们使用的训练数据必须是成对或三元组的，并且这些对或组的相似性标签是已知的，相似/不相似是训练的输入（Ground Truth），而具有语义意义的距离 \(D\) 是训练的输出和最终推理的依据。

【2】为什么在已知“相似/不相似”的情况下，还要追求距离的变化：

传统的分类任务学习一个决策边界，将不同类别的样本分隔开。但是度量学习任务学习一个嵌入空间（Embedding Space），使空间中的距离具有语义意义。

传统分类只能回答“是不是猫”。度量学习要回答的是“这只猫和那只猫有多像？”。只有通过距离，我们才能量化这种程度。假设你训练了 100 种动物的分类器。来了一只新动物“袋鼠”，传统分类器无能为力。但在度量学习中，如果模型学会了将所有有袋动物都映射到空间中的一个区域，那么这只新袋鼠就会落在那个区域，通过计算它与现有样本的距离，我们就能判断它的相似性和类别。

在搜索引擎或推荐系统中，我们输入一张图片 \(A\)，希望找到最相似的 \(K\) 张图片。这需要计算 \(A\) 的嵌入向量与数据库中所有嵌入向量的距离，然后按距离从小到大排序。如果模型只是简单地输出“相似”或“不相似”，就无法进行排序。

追求距离的变化，是为了让这个嵌入空间具备泛化能力和可度量性（Metricity），从而支持基于相似度的检索、聚类和验证等高级任务。

【3】一旦模型训练完成，在实际应用（推理）时，我们就不再需要这个 \(Y\) 标签了。我们只输入两张图片 \(A\) 和 \(B\)，模型输出它们的距离 \(D_{A,B}\)。这个距离 \(D_{A,B}\) 就是模型对它们相似程度的预测。

总结来说：

  • 训练时： \(Y\) 已知 (输入/标签)。
  • 推理时： \(Y\) 未知 (通过计算距离 $D$ 来预测相似度)。

除了对比损失，还有三元组损失和余弦相似度损失。

三元组损失：作用于三元组（锚点、正例、负例），以强制执行相对距离。比对比损失更强大。它要求锚点（Anchor）到正例（Positive）的距离，必须比锚点到负例（Negative）的距离至少小一个边际值。这确保了相似样本被更好地聚类。

余弦相似度损失：在角度空间中最大化正样本对之间的相似度。这类损失使用余弦相似度而非欧氏距离，更关注嵌入向量的方向而不是长度。它将所有嵌入点都视为在单位超球体上，优化它们的相对角度。

3.2损失函数的区别与对比

任务类型 损失函数举例 目标 特点
分类 (Classification) 交叉熵（Cross-Entropy）/KL 距离 最小化预测概率分布与真实标签分布之间的距离。 关注单个样本的类别标签。
回归 (Regression) 均方误差（MSE）/欧氏距离 最小化预测值与真实值之间的数值差异。 关注单个样本的数值输出。
度量学习 (Metric Learning) 对比损失（Contrastive Loss） 最小化相似样本对的距离，最大化不相似样本对的距离。 关注样本对或三元组之间的相对距离。

3.3嵌入向量

【1】什么是嵌入？

嵌入是连续空间中对象的向量表示。 想象一个坐标系，每个对象（词语、图像、用户）都被表示为一个坐标点，这个坐标就是嵌入向量。每个数据点都被映射到一个低维向量，该向量捕获了它的语义意义。

如果两个词的意义相似（如“国王”和“女王”），它们在嵌入空间中的向量就会非常接近。

【2】嵌入向量：

嵌入向量（Embedding Vector）就是模型在最后一层或倒数第二层的输出，它代表了输入数据的低维、密集且富有语义信息的特征表示。

输入 \(X\) \(\rightarrow\) 通过模型的各个隐藏层（卷积、池化、激活等操作） \(\rightarrow\) 得到高级特征 \(\rightarrow\) 通过最后的嵌入层（全连接层） \(\rightarrow\) 输出嵌入向量 \(\text{vector}\)。

度量学习中的 嵌入向量（Embedding Vector） 和 OpenAI 的 Embedding 模型（例如 text-embedding-3-small 或 text-embedding-ada-002）在概念和功能上是完全一致的，它们都代表了将数据映射到语义空间的核心思想。

度量学习中的嵌入向量是将输入样本（如图片 \(X\)）通过训练的模型 \(f\) 映射得到的低维向量 \(f(X)\)，确保语义相似的样本对在嵌入空间中距离近，本质是将高维、稀疏或复杂的原始数据转换为密集、连续的语义表示。

而OpenAI 的 Embedding 模型将输入文本（如句子 \(T\)）通过预训练的模型 \(f\) 映射得到的低维向量 \(f(T)\)，确保语义相关的文本段落在嵌入空间中距离近。OpenAI 的 Embedding 模型是大规模、通用的文本度量学习模型的结果。它提供了一个预训练好的特征提取器 \(f\)，让用户可以直接跳过复杂的训练步骤，将文本转化为具有语义意义的嵌入向量，并直接在应用中使用我们前面讨论的距离计算进行检索和相似度判断。

3.4代码

我们将使用 scikit-learn 嵌入和简单的三元组方法来说明。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

import numpy as np
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
from sklearn.metrics.pairwise import euclidean_distances

# Load Iris dataset
iris = load_iris()
X = iris.data
y = iris.target

# Standardize features
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# Create embeddings (for simplicity, use the raw scaled features as embeddings)
embeddings = X_scaled

# Example: Find most similar item to the first sample
anchor = embeddings[0]  # 选取第一个样本作为锚点（Anchor），即我们要查找相似项目的目标。
# 计算锚点与数据集中所有样本（包括它自己）之间的欧氏距离。结果 distances 是一个包含 150 个距离值的数组
distances = euclidean_distances([anchor], embeddings)[0]
# (排除锚点自身)查找最近邻,因为锚点到自身的距离总是 0，但这没有意义
closest_idx = np.argmin([d if i !=0 else np.inf for i,d in enumerate(distances)])

print("Anchor label:", y[0])
print("Closest label:", y[closest_idx])
print("Distance:", distances[closest_idx])

代码使用著名的 Iris（鸢尾花）数据集，它包含 150 个样本，每个样本有 4 个特征（花萼/花瓣的长度和宽度），以及 3 个类别标签（0, 1, 2）。

对特征数据进行标准化。标准化是必要的预处理步骤，它将每个特征的均值变为 0、标准差变为 1，防止量纲差异影响距离计算。

直接将标准化后的原始特征 X_scaled 视为嵌入向量（Embeddings）。(embeddings = X_scaled)

代码会输出锚点样本的类别、距离最近样本的类别以及它们之间的距离

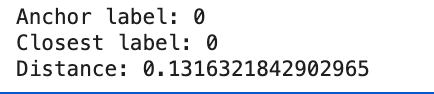
image-20251124141318756

Iris 样本的 4 个标准化后的特征 \([X_1, X_2, X_3, X_4]\) 构成了它的嵌入向量。这是度量学习的基础 。距离计算（欧氏距离）是度量相似性的核心。距离越小，相似度越高。

真正的度量学习会训练一个复杂的神经网络（一个非线性转换函数），这个网络负责学习最好的特征表示，确保同一个类别的样本（相似点）距离比不同类别的样本（不相似点）更近。

在人脸识别等任务中，深度学习模型通过 Triplet Loss 或 Contrastive Loss 不断调整其内部参数，从而生成具有高区分度的嵌入向量。例如，即使两个人脸图像的姿态和光照不同，只要是同一个人，它们的嵌入距离也会非常小。

3.5度量学习的局限

只能用来判断相似，不能用来判断不相似的正确性

度量学习模型在识别相似样本（Positive Case）方面表现出色，但它在确认不相似样本（Negative Case）的“真实性”或“正确性”方面是受限的。

模型是在一个由训练数据定义的语义空间内进行度量。对于落在语义空间边界之外的输入，模型只能将其判定为“不相似”或“距离很远”，但无法判断这个“不相似”的输入是否具有有效性、真实性或正确性。

如果攻击者使用一个模型从未见过的高级合成人脸（Deepfake），模型可能只会判断“不相似”，但无法确定这是“欺诈”还是“新用户”，需要额外的活体检测或异常检测系统来辅助判断输入 \(C\) 本身的正确性。

搜索结果中出现一个距离很远的项，可能是因为它不相似，也可能是因为它是系统无法理解的垃圾数据。

度量学习提供了一个强大的比较工具，但它本身不是一个验证工具。它擅长回答“它们是否一致？”，但不擅长回答“这个输入本身是否有效且正确？”。为了解决这个局限，通常需要将度量学习与传统的分类或异常检测技术结合使用。

3.6使用场景

推荐系统是一个典型的大数据问题。假设商品数量 \(N=10000\) 个，目标是从中找到 \(K=10\) 个用户最喜欢的。直接计算个商10000品与用户之间的精确关系是非常耗时的。因此，需要分两步走。

  • 召回（recall）：快速、高效地从海量数据中筛选出用户可能喜欢的少数候选集
  • 排序（rank）：在召回的 100 个候选商品中，使用更复杂的模型进行精细化打分，找出用户最喜欢的 10 个（优中选优）。

目前2个方案：

  • 度量学习/孪生网络：高效率，低精度要求

image-20251124143258719

  • DNN：充分的特征交叉，模型能够学习用户和商品特征之间复杂、非线性的交互关系，低效率可接受，高精度要求，效果是更好的

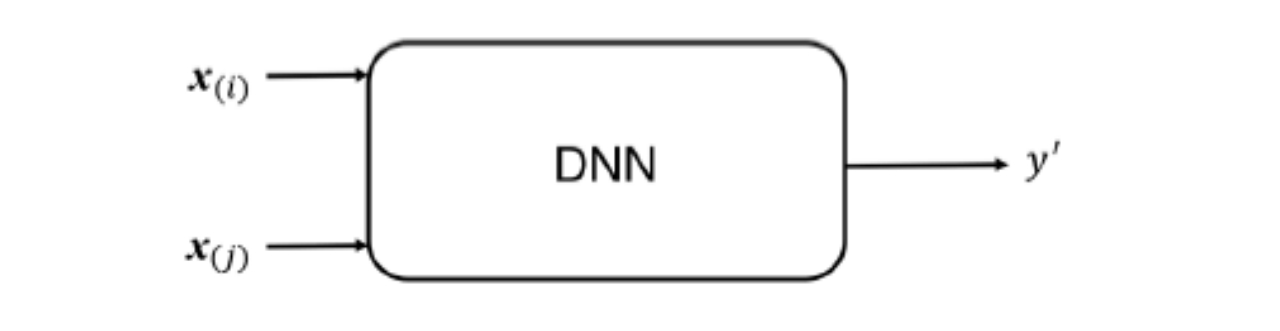
image-20251124143312547

度量学习（方案 1）擅长处理海量数据下的相似性检索，能以高效率完成快速筛选（召回）任务。

方案 2 的计算复杂度高，但在小集合（100个）上能提供极高的准确性和排序精度。

这种“粗排（召回）+ 精排（排序）”的两阶段策略，是所有大规模推荐系统在保证用户体验（高精度）和系统性能（高效率）之间寻求平衡的最佳实践。

3.7推荐的项目/框架

YouTube DNN（特指其在 2016 年论文《Deep Neural Networks for YouTube Recommendations》中提出的两阶段深度学习架构）在推荐系统领域，确实是度量学习的一个里程碑式的集大成者，但它不再是目前最尖端的单一技术。

原始的 DNN 模型相对简单，后来的推荐系统采用了更复杂的模型来替代或增强它，包括：

  • Wide & Deep Learning: 结合了浅层记忆能力和深度泛化能力。
  • Transformer 模型： 利用自注意力机制（Self-Attention）来捕捉用户行为序列中的复杂依赖关系，在序列建模上表现远超 DNN。
  • Graph Neural Networks (GNNs): 利用用户-物品交互图中的连接信息来生成更精确的嵌入。

可以说，YouTube DNN 奠定了现代推荐系统的基石，它将度量学习从理论推向了工业实践的巅峰。但现在，它的具体架构已经被更新、更复杂的 Transformer、GNN、多任务学习等技术所取代或吸收。

CATALOG
    FEATURED TAGS
    书籍阅读 算法 人工智能AI基础 python基础 力扣 AI思想启蒙 numpy pandas 机器学习-吴恩达 机器学习算法 matplotlib spring6 算法题库 Java基础 java集合 ollama工具 python爬虫
    FRIENDS