1.机器学习中最大的难点
特征!特征!特征!
一个好的特征,即使最简单的逻辑回归,也能出色的完成任务
好特征的标准:
- 区分性强:特征值在不同类别之间应有显著差异,而在同一类别内部应保持相似。
- 特征多:特征的数量并非越多越好,而是要尽可能覆盖目标变量的所有影响因素。
- 特征的各类组合:有的时候看基础特征进行分类,意义不大。但是特征组合就很厉害。比如双十一时期,二三十岁的女性。需要升维(特征组合等)/使用非线性的模型(比如FM,深度学习等)
在实际工作中,数据科学家通常将 70% 的时间投入到特征工程中,因为这是决定项目成败的关键。
FM模型自动学习两两特征之间的潜在交互强度,但是只能组合二阶特征,更高阶的组合仍需手动定义或忽略。
借鉴FM模型,我们可以提供特征组合的框架,具体组合方式,由模型自动学习
2.一层神经网络
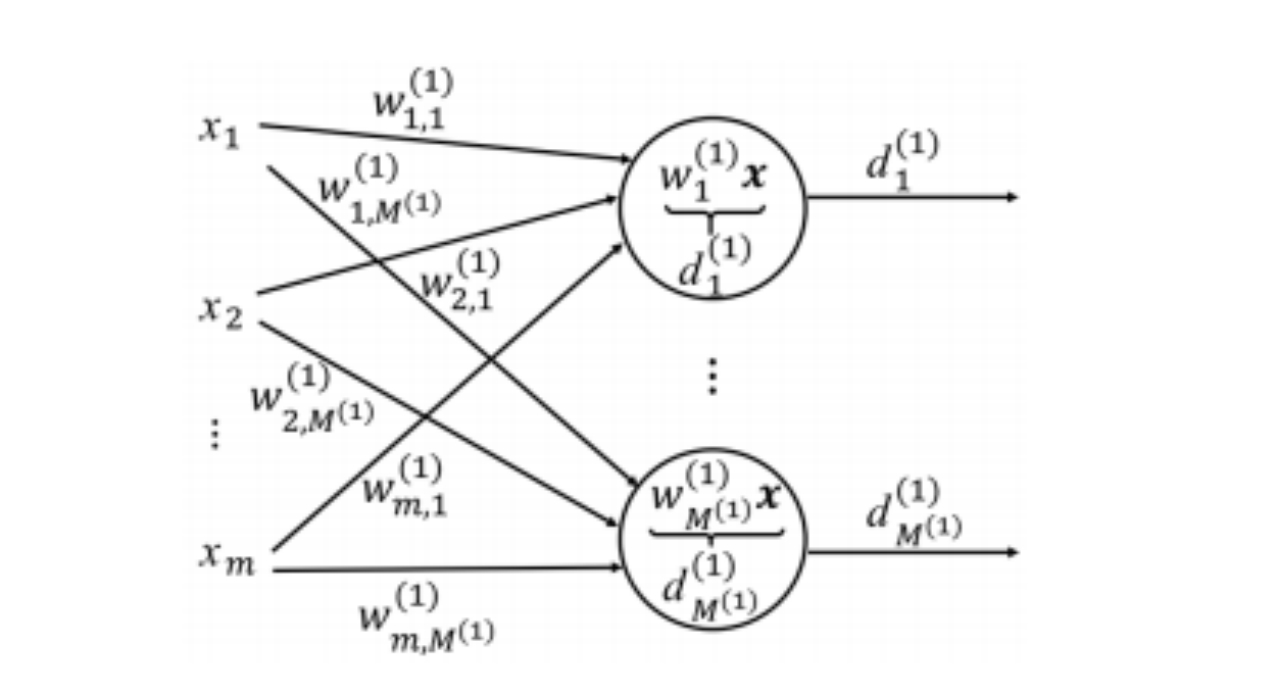
每个d都由所有x加权求和组成,权重为自动学习,即输出层的每个神经元,都是输入层所有特征的加权求和。
一层神经网络(通常也称为单层感知机或无激活函数的全连接层)
这个网络模型由输入层和输出层(隐藏层)组成。
- 输入向量 \(x\):
- 表示 \(m\) 个输入特征,\(x = [x_1, x_2, \dots, x_m]^T\)。
- 它们是模型接收的原始数据点。
- 输出向量 \(d^{(1)}\):
- 表示 \(M^{(1)}\) 个神经元的输出,\(d^{(1)} = [d_1^{(1)}, d_2^{(1)}, \dots, d_{M^{(1)}}^{(1)}]^T\)。
- 上标 \(^{(1)}\) 表示这是第一层(通常也是唯一一层隐藏层)的输出。
对于输出层的第 \(j\) 个神经元 \(d_j^{(1)}\) 而言:
\[d_{j}^{(1)} = w_{j,1}^{(1)} x_{1} + \dots + w_{j,m}^{(1)} x_{m}\]- \(w_{j,i}^{(1)}\):是连接输入特征 \(x_i\) 到输出神经元 \(d_j^{(1)}\) 的权重 (Weight)。这个权重衡量了输入 \(x_i\) 对输出 \(d_j^{(1)}\) 的重要性或贡献度。
标准的神经网络计算通常还会包括一个偏置项 \(b_j\),即 \(d_j^{(1)} = (\sum_{i=1}^{m} w_{j,i}^{(1)} x_{i}) + b_{j}^{(1)}\)。图中为了简化表示,省略了偏置项。
矩阵形式的表达(效率和抽象)
将所有 \(M^{(1)}\) 个神经元的计算过程抽象为一个矩阵运算,更加简洁高效:
\[d^{(1)} = W^{(1)} x\]
- 权重矩阵 \(W^{(1)}\): 这是一个 \(M^{(1)} \times m\) 维度的矩阵,包含了所有连接权重 \(w_{j,i}^{(1)}\)。
- 矩阵的每一行对应一个输出神经元 \(d_j^{(1)}\)。
- 矩阵的每一列对应一个输入特征 \(x_i\)。
- 矩阵乘法 \(W^{(1)} x\) 实现了所有神经元同时进行加权求和的计算。
这个模型的目标就是通过学习,找到最优的权重矩阵 \(W^{(1)}\),使得模型的预测输出最接近真实值。
学习过程:
- 模型计算当前权重下的输出 \(d^{(1)}\)。
- 计算输出与真实标签之间的损失 (Loss)。
- 通过梯度下降 (Gradient Descent) 等优化算法和反向传播 (Backpropagation) 机制,计算损失对每个权重 \(w_{j,i}^{(1)}\) 的梯度(即偏导数)。
- 根据梯度来更新和调整权重 \(W^{(1)}\),使损失函数减小。
如果这个“一层神经网络”的输出 \(d^{(1)}\) 直接作为最终输出,并且没有使用非线性激活函数,那么这个模型本质上执行的是一个线性变换:
- 作为线性模型: 如果 \(M^{(1)}=1\)(只有一个输出神经元),并且在其上加一个 Sigmoid 激活函数,它就退化成一个逻辑回归 (Logistic Regression) 分类器。
- 作为特征提取器: 在多层网络中,这一层被称为隐藏层。它将原始的 \(m\) 维输入特征 \(x\) 映射到了一个新的 \(M^{(1)}\) 维特征表示 \(d^{(1)}\)。这个新的 \(d^{(1)}\) 包含了原始特征的线性组合信息,为后续更深层的非线性处理奠定了基础。
2.1维度转换
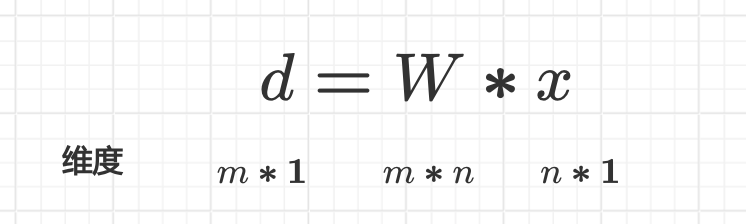
- \(m > n\),升维/维度扩展,增加数据点的线性可分性,提高分辨能力
- \(m < n\),降维/维度压缩,特征中可能包含大量冗余、噪声或不相关的特征,去除无用数据
一般的神经网络,一般都是先升维然后降维。
2.2非线性变换
加权后,还需要进行非线性变换 (激活函数)
\[a^{(1)} = f(d^{(1)} + w0^{(1)}) = \begin{bmatrix} f(d_1^{(1)} + w0_1^{(1)}) \\ \vdots \\ f(d_{M^{(1)}}^{(1)} + w0_{M^{(1)}}^{(1)}) \end{bmatrix}\] \[a^{(1)} = f(d^{(1)} + w0^{(1)})\]- \(d^{(1)}\): 这是前一步骤的线性输出。 \(d^{(1)} = W^{(1)} x\)。
- \(w0^{(1)}\): 这是该层的偏置项 (Bias),通常记为 \(b^{(1)}\)。在向量形式中,\(w0^{(1)}\) 就是 \(b^{(1)}\) 向量,维度与 \(d^{(1)}\) 相同。
- \(d^{(1)} + w0^{(1)}\): 这构成了神经元完整的净输入 (Net Input) 或加权和。
- \(f(\cdot)\): 这就是激活函数 (Activation Function),它是一个非线性函数。
- \(f(\cdot)\) 被逐元素(element-wise)地应用到净输入向量的每个分量上。
- \(a^{(1)}\): 这是该层的激活输出 (Activation Output),也是下一层的输入特征。
为什么要“一定要进行非线性变换”?
这是深度学习中最重要的概念之一。如果神经网络中不使用任何激活函数(即 \(f(x)=x\),使用线性函数),那么无论网络堆叠多少层,整个网络最终都等同于一个单一的线性模型。
假设我们有一个两层网络,都只使用线性变换:
- 第一层输出 (线性): \(d^{(1)} = W^{(1)} x\)
- 第二层输出 (线性): \(d^{(2)} = W^{(2)} d^{(1)}\)
将 \(d^{(1)}\) 代入 \(d^{(2)}\) 中:
\[d^{(2)} = W^{(2)} (W^{(1)} x)\]根据矩阵乘法的结合律,我们可以定义一个新的矩阵 \(W_{\text{new}} = W^{(2)} W^{(1)}\):
\[d^{(2)} = W_{\text{new}} x\]结论: 无论堆叠多少层线性层,整个网络的输出始终是输入 \(x\) 的一个线性函数 \(W_{\text{new}} x\)。
线性模型(如逻辑回归)只能找到一个直线或平面作为决策边界,无法拟合现实世界中大量存在的非线性关系(例如圆圈、S 形、复杂曲线等)。 如果没有非线性,堆叠再多的层也无法增强模型的表达能力。
激活函数通过引入非线性,为神经网络赋予了强大的能力:
- 允许网络拟合任意复杂的函数。这是区分深度学习与传统线性模型的关键。
- 每一层激活函数后的输出 \(a^{(1)}\) 都是非线性组合后的新特征,这些特征比原始输入具有更高的抽象层次和更强的区分性。
- 激活函数(尤其是 Sigmoid 和 Tanh)最初是为了模仿生物神经元“阈值触发”的机制,即当净输入超过某个阈值时,神经元才被激活。
2.3常见的非线性激活函数
(1)Sigmoid:将输出压缩到 \((0, 1)\) 区间,常用于二分类输出层。但容易导致梯度消失。
\[f(z) = \frac{1}{1 + e^{-z}}\](2)Tanh:将输出压缩到 \((-1, 1)\) 区间,输出均值更接近 0,收敛速度通常比 Sigmoid 快。
\[f(z) = \frac{e^z - e^{-z}}{e^z + e^{-z}}\](3)ReLU:最常用。计算简单(只有阈值判断),有效解决了梯度消失问题,加速了网络训练。
\[f(z) = \max(0, z)\]2.4两层神经网络
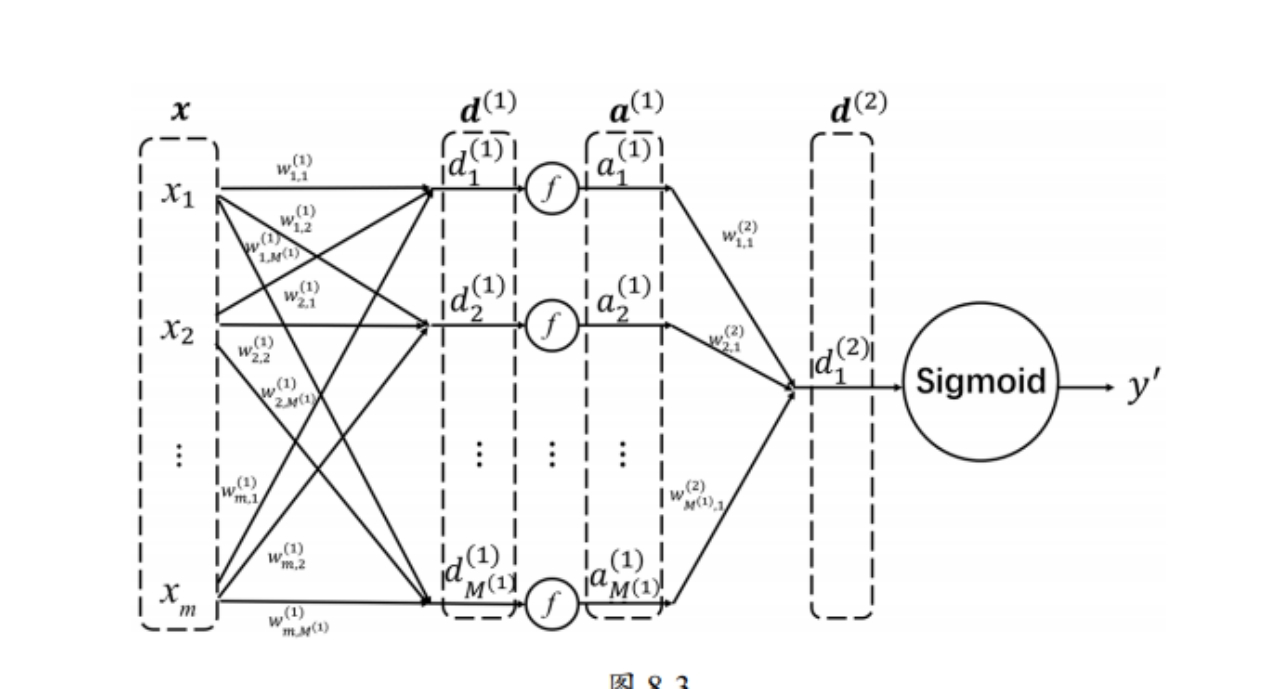
输入层 \(x\): 包含 \(m\) 个特征 \(x_1\) 到 \(x_m\)。
第一层(隐藏层/全连接层): 进行了两次操作。是整个网络的核心,它实现了之前讨论的特征工程自动化。
- 线性加权和 (Weighted Sum): 从 \(x\) 到 \(d^{(1)}\)。\(d^{(1)} = [d_1^{(1)}, d_2^{(1)}, \dots, d_{M^{(1)}}^{(1)}]^T\),其中\(d_{j}^{(1)} = w_{j,1}^{(1)} x_{1} + \dots + w_{j,m}^{(1)} x_{m}\)。
- 非线性激活 (Activation): 从 \(d^{(1)}\) 到 \(a^{(1)}\),通过激活函数 \(f\) 实现。\(a^{(1)} = f(d^{(1)} + w0^{(1)})\)
- 这是一个线性变换,将 \(m\) 维的原始输入 \(x\) 映射到一个 \(M^{(1)}\) 维的新空间 \(d^{(1)}\)。这一步完成了所有特征的线性交叉和重组。
“全连接层”是基于它的结构(拓扑)命名的;而“隐藏层”是基于它的位置(功能)命名的。
在大多数情况下,一个隐藏层同时也是一个全连接层,因此这两个术语经常互换使用。
- “隐藏”是因为这层神经元的输入和输出既不是直接的原始输入 \(x\),也不是最终的预测输出 \(y'\),而是位于输入和输出之间的层。只有位于输入层和输出层之间的层才能被称为隐藏层。一个网络可以有零个、一个或多个隐藏层。
- “全连接”是描述这一层神经元之间的连接拓扑结构。在一个全连接层中,该层的每一个神经元都与前一层的所有神经元(或输入特征)相连接。这种结构在数学上体现为矩阵乘法 \(d = Wx\)。绝大多数神经网络(如 MLP)的隐藏层都是全连接层。网络的最终输出层(例如分类器的 Softmax 层之前)通常也是一个全连接层。像卷积神经网络(CNN)中的卷积层 (Convolutional Layer) 就不是全连接层,因为卷积核只连接到前一层特征图的局部区域。
第二层(输出层): 同样进行了两次操作。
- 线性加权和: 从 \(a^{(1)}\) 到 \(d^{(2)}\)。引入非线性,使得新的特征表示 \(a^{(1)}\) 能够捕捉输入特征之间非线性的、高阶的复杂关系。向量 \(a^{(1)}\) 是由 \(M^{(1)}\) 个高度抽象的、非线性组合的新特征构成,这些特征是模型自动从数据中学习到的。“自动”体现在模型无需人类预先设计任何特征组合规则,完全依靠数据驱动来找到最佳的特征表示。
- 非线性激活 (Sigmoid): 从 \(d^{(2)}\) 到最终的预测输出 \(y'\)。
3.反向传播 (Backpropagation)
BP 是反向传播 (Backpropagation) 的缩写,它是一种用于训练多层前馈神经网络的高效算法。
- 前向传播 (Forward Pass): 从 \(x\) 到 \(y'\) 计算一次预测值。
- 计算损失 (Loss): 根据 \(y'\) 和真实标签 \(y\) 计算误差 \(L\)。
- 反向传播 (Backward Pass): 利用链式法则(Chain Rule),将损失 \(L\) 的梯度(导数)从输出层 \(y'\) 逐层向后传递,计算出每一层(\(W^{(2)}\) 和 \(W^{(1)}\))的权重对总损失的贡献。
- 权重更新: 利用优化器(如 SGD 或 Adam),根据计算出的梯度来更新和调整所有权重矩阵 $W^{(1)}$ 和 $W^{(2)}$,使损失最小化。
优化器(Optimizer)的主要任务是:根据反向传播计算出的梯度,智能地调整神经网络中的所有参数(权重 \(W\) 和偏置 \(b\)),使得损失函数 \(L\) 的值持续下降。
4.为什么一定要激活函数
第一:防止深度丧失意义。
没有激活函数的两层线性变换,真的没有一点意义吗?
有意义,减少了大量的参数
而且参数量的大幅减少,相当于引入了一种正则化 (Regularization)。参数越少,模型的自由度越低,它越难在训练数据上“死记硬背”,从而有效降低了模型在小样本数据集上的过拟合 (Overfitting) 风险。
参数越少,每次反向传播计算梯度和更新权重所需的时间就越短,从而加速了模型的训练过程,提高了计算效率。
总结:虽然添加非线性激活函数是赋予神经网络强大拟合能力的关键,但没有激活函数的两层线性变换仍有其明确的价值,尤其是在工程实践中:它通过引入一个低维的中间层,在不改变模型最终线性表达能力的前提下,极大地减少了参数量,从而提高了模型的泛化能力和训练效率。
第二,根据泰勒公式,线性变换(加权求和 \(z = Wx+b\)):是神经网络中没有激活函数时的计算形式,二阶以后 全都为0,这意味着无论我们如何堆叠线性层,它始终只能表达 \(x\) 的一阶关系,无法逼近任何复杂的非线性函数。
但是合适的非线性变换(常见的激活函数) :高阶导数都不为0,尽可能保留高阶项。非线性激活函数(如 Sigmoid, Tanh, ReLU)的引入,使得函数可以逼近任意复杂的非线性函数。这些高阶项赋予了神经网络拟合曲线、圆环、螺旋线等非线性决策边界的能力(相当于做了高阶特征组合)。这正是万能逼近定理(Universal Approximation Theorem)的数学基础:一个具有至少一个隐藏层和非线性激活函数的神经网络,理论上可以无限逼近任何连续函数。
【补充】泰勒公式及其展开式:
\[f(x) = \frac{f(a)}{0!} + \frac{f'(a)}{1!}(x-a) + \frac{f''(a)}{2!}(x-a)^2 + \dots + \frac{f^{(n)}(a)}{n!}(x-a)^n + R_n(x)\]关键注释:
- 任何函数都可以写成多项式的和。
- \(a\) 是函数定义域上的任意一点,\(x\) 在 \(a\) 的附近。
- \(R_n\) 是余项;\(n\) 越大,\(R_n\) 越小;当 \(n \to \infty\) 时,\(R_n \to 0\)。
为什么\(f(x)=e^x\)很少作为激活函数?
虽然 \(e^x\) 是一个非线性函数,且在数学上性质优良,但在实际的神经网络训练中,它存在两个致命的缺陷,使其难以作为通用的激活函数。
【问题1】梯度爆炸问题
在神经网络的前向传播中,如果神经元的净输入 \(z\) 稍微偏大,例如 \(z = 10\),那么 \(f(z) = e^{10} \approx 22000\)。
在反向传播中,梯度会乘以激活函数的导数 \(f'(z)\)。
如果 \(z=10\),导数 \(f'(10) = e^{10} \approx 22000\)。
由于指数函数增长得非常快,一旦网络中的某个权重或输入使净输入 \(z\) 稍大,反向传播的梯度就会被这个巨大的导数放大,导致梯度在层间传递时急剧增大,即梯度爆炸。
梯度爆炸会导致网络权重更新幅度过大,模型参数快速震荡,损失函数变为 NaN(Not a Number),使训练过程彻底崩溃。
【问题2】输出非零均值
\(f(x) = e^x\) 的值域是 \((0, +\infty)\),函数值永远是正数。
隐藏层的输出 \(a^{(l)}\)(即下一层的输入 \(x^{(l+1)}\))总是正的。
这意味着,下一层的净输入 \(z^{(l+1)} = W^{(l+1)} a^{(l)} + b^{(l+1)}\) 对梯度的影响是同向的。
当所有输入 \(a^{(l)}\) 都是正数时,下一层 \(W^{(l+1)}\) 的梯度计算(\(\partial L / \partial W\))要么全部是正的,要么全部是负的。这使得梯度更新方向被局限在特定的象限内,无法直接朝向最优解的方向。这会减慢梯度下降的效率和收敛速度。
5.softmax函数
Softmax 函数的公式和计算原理
将净输入 \(d^{(L)} + w0^{(L)}\) 向量转换为概率向量 \(y'\)。
\[y' = \text{Softmax}(d^{(L)} + w0^{(L)}) = \frac{1}{\sum_{m=1}^{C} e^{d_m^{(L)} + w0_m^{(L)}}} \begin{bmatrix} e^{d_1^{(L)} + w0_1^{(L)}} \\ \vdots \\ e^{d_C^{(L)} + w0_C^{(L)}} \end{bmatrix}\]Softmax 软分类(可求导),而max是一种硬分类(不可导)。
在机器学习中,函数求导是一件很重要的事情—->softmax比max更好
可导性是进行反向传播和梯度下降的前提。Max 函数无法提供梯度来指导模型如何修正错误。
Softmax 提供了“软”的决策边界,有利于平滑训练。
Softmax 在只有 2 个类别时的简化版本,等价于 Sigmoid 函数。
https://kirsten-1.github.io/2025/11/20/AI%E6%80%9D%E6%83%B3%E5%90%AF%E8%92%9906/
二分类 Softmax 严格等价于 Sigmoid 函数,这证明了 Softmax 是 Sigmoid 在多分类场景下的泛化。
