
1.先验概率和后验概率
先验概率是根据经验得到的,比如看摊位买的西瓜,大致认为60%的概率西瓜是好的。先验概率不需要样本数据,不受任何条件的影响。不根据其他,就根据常识大致判断。
而后验概率就类似于看瓜蒂脱落与否判断西瓜是否是好的。
计算后验概率就是朴素贝叶斯最核心的一步。
联合概率是几个事件同时发生的概率。例如P(瓜熟, 瓜蒂脱落)就是一个联合概率
P (瓜熟,瓜蒂脱落) =P (瓜熟|瓜蒂脱落) *P (瓜蒂脱落)
P(瓜熟,瓜蒂脱落) =P(瓜蒂脱落|瓜熟) *P(瓜熟)
| 但是要求的是$$P(\text{瓜熟 | 瓜蒂脱落})$$: |
| $$P(\text{瓜熟 | 瓜蒂脱落}) \times P(\text{瓜蒂脱落}) = P(\text{瓜蒂脱落 | 瓜熟}) \times P(\text{瓜熟})$$ |
| $$P(\text{瓜熟 | 瓜蒂脱落}) = \frac{P(\text{瓜蒂脱落 | 瓜熟}) \times P(\text{瓜熟})}{P(\text{瓜蒂脱落})}$$ |
| 因为$$P(\text{瓜蒂脱落 | 瓜熟})\(和\)P(\text{瓜熟})\(是已知的,所以只需要求出\)P(\text{瓜蒂脱落})$$即可。 |
而P(瓜蒂脱落) = P(瓜蒂脱落|瓜熟) * P(瓜熟) + P(瓜蒂脱落|瓜生) * P(瓜生)(全概率公式)
| 若已知P(瓜熟)=0.6,P(瓜蒂脱落 | 瓜生)=0.,P(瓜生)=0.4,P(瓜蒂脱落 | 瓜熟)=0.8 |
则P(瓜熟/瓜蒂脱落) = (0.8*0.6) / (0.8*0.6+0.4*0.4) =0.75
如果特征很多(各个特征之间是独立的),那么可以这么计算:
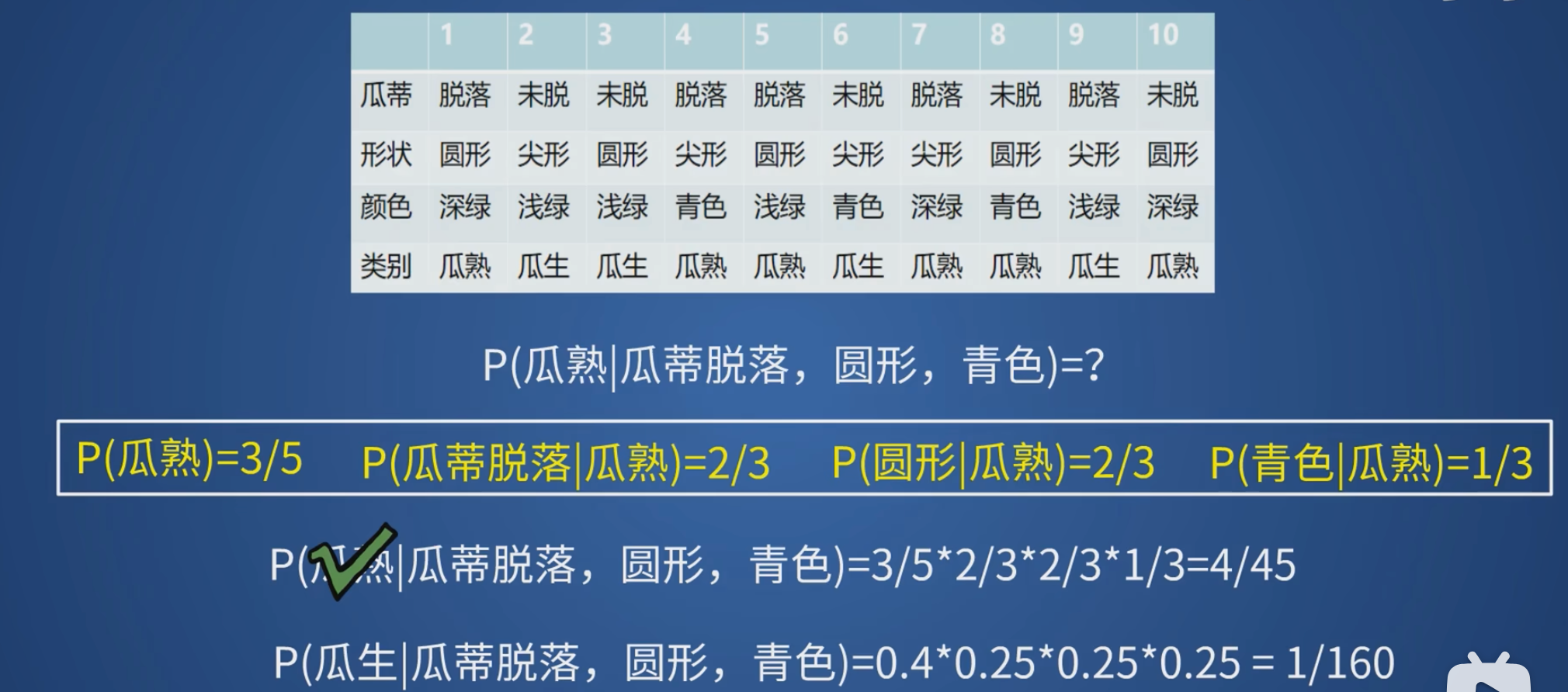
以上就是朴素贝叶斯算法的一个应用。
2.朴素贝叶斯算法
| 朴素贝叶斯(Naive Bayes)是一种基于贝叶斯定理的生成模型。它通过计算后验概率 $$P(\text{类别} | \text{特征})$$ 来进行分类。 |
贝叶斯公式是其理论基础:
\[P(\text{类别}| \text{特征}) = \frac{P(\text{特征}| \text{类别}) \times P(\text{类别})}{P(\text{特征})}\]- \(P(\text{类别})\) (先验概率): 这是在观察任何特征之前,我们对某一类别概率的预估(如您所说,比如上面例子中\(P(\text{瓜熟})=0.6\))。
-
**$$P(\text{特征} \text{类别})\((似然项):** 在类别已知的情况下,观察到特征的概率(如\)P(\text{瓜蒂脱落} \text{瓜熟})=0.8$$)。 - \(P(\text{特征})\) (证据项): 观察到特征本身的概率,通过全概率公式计算得出(如 \(P(\text{瓜蒂脱落})\))。
-
**$$P(\text{类别} \text{特征})\((后验概率):** 这是最终要求的,在特征已知的情况下,类别发生的概率(如\)P(\text{瓜熟} \text{瓜蒂脱落})=0.75$$)。
2.1“朴素”的含义:特征独立性假设
在实际的机器学习问题中,特征 \(x\) 往往不止一个,而是多个特征向量 \(x = (x_1, x_2, \dots, x_n)\)。
朴素贝叶斯名字中的“朴素”指的是它做了一个强假设:所有特征之间相互独立。
在类别 \(y\) 已知的情况下,所有特征的联合概率等于它们各自概率的乘积。
\[P(x_1, x_2, \dots, x_n | y) = P(x_1|y) \times P(x_2|y) \times \dots \times P(x_n|y)\]这个“朴素”的假设大大简化了计算,使得模型可以在特征数量非常大时依然高效运行,但这也是它牺牲模型准确性的地方(因为现实中特征很少是完全独立的)。
2.2朴素贝叶斯与逻辑回归、线性回归的对比
| 特性 | 朴素贝叶斯 (Naive Bayes) | 逻辑回归 (Logistic Regression) | 线性回归 (Linear Regression) |
|---|---|---|---|
| 模型类型 | 生成模型 (Generative Model) | 判别模型 (Discriminative Model) | 判别模型 (Discriminative Model) |
| 解决问题 | 分类 (Classification) | 分类 (Classification) | 回归 (Regression) |
| 目标输出 | 离散的类别标签 (如“好瓜”/“坏瓜”) | 类别概率 | 连续值 |
| 优点 | 训练速度极快;对缺失数据不敏感;对数据量较小的场景有效。 | 输出是概率值,可解释性强;决策边界是线性的;理论基础坚实。 | 模型简单且可解释性强;计算高效。 |
| 缺点 | 因为强大的特征独立性假设,但是独立性假设往往不成立,可能牺牲准确率。 | 易受异常值影响;只能解决线性可分或近似线性的问题。 | 只能拟合线性关系;对噪声和多重共线性敏感。 |
3.缺失值的处理
比如婚恋相亲网站,每个用户信息填写的完整程度不同(用户填写意愿、隐私考量或信息复杂性)。在推荐/匹配/预测场景(机器学习)中,如果碰到缺失值如何处理?
处理缺失值的方法大致可以分为三类:删除(Deletion)、插值/填充(Imputation)、和建模(Modeling)。
3.1删除
当缺失量极少或缺失模式很随机时可以考虑。
| 方法 | 描述 | 适用场景 | 风险/缺点 |
|---|---|---|---|
| 1. 行删除 (Listwise Deletion) | 直接删除任何包含缺失值的样本(用户记录)。 | 缺失值占总数据量比例极低(如 < 1%)且缺失是完全随机的。 | 如果缺失值较多,会导致数据量急剧减少,损失大量信息,引入偏差。 |
| 2. 列删除 (Feature Deletion) | 如果某个特征(如“年收入”)的缺失率极高(如 > 90%),则直接删除该特征。 | 该特征对核心业务价值不大,且缺失率高到无法有效填充。 | 可能丢失对模型有潜在价值的信息。 |
3.2填充
用某种值替换缺失值,这是最常用的方法。
| 方法 | 描述 | 适用场景 | 风险/缺点 |
|---|---|---|---|
| 3. 均值/中位数/众数填充 | 数值特征(如身高、年龄):用均值或中位数填充。类别特征(如学历、信仰):用众数填充。 | 缺失值比例适中,或缺失是随机的。 | 这种方法会减小特征的方差,并引入偏差(特别是均值填充),使数据分布失真。 |
| 4. 哨兵值填充 (Sentinel/Flag Value) | 用一个特定的值(如 -999 或 Unknown)来标记缺失,让模型知道这个值是缺失的。 |
特别适用于类别特征,或当缺失本身可能包含信息(e.g., “不愿填写”本身就是一种信息)。 | 模型可能会错误地将这个哨兵值解释为一个“正常”的极大或极小值。 |
| 5. 基于模型填充 (Model-based Imputation) | 使用其他非缺失特征作为输入,训练一个模型(如线性回归、决策树、KNN 等)来预测缺失值。 | 缺失值数量较大,且特征之间有较强相关性。 | 填充值更接近真实数据分布,精度高。常用的方法有 MICE(多重插值)和 KNN Imputation。 |
|---|---|---|---|
| 6. 前后值填充 (Locally based Imputation) | 对于时间序列数据(不适用于相亲网站的静态数据),用前一个或后一个观测值填充。 | 数据存在时间或空间上的连续性。 | 不适用于独立的个人信息记录。 |
3.3建模
不直接改变数据,而是修改模型或增加信息。
| 方法 | 描述 | 适用场景 | 优点 |
|---|---|---|---|
| 7. 缺失指示变量 (Missing Indicator) | 对于每个有缺失值的特征X,增加一个二元指示变量I。如果 X缺失,则I=1,否则 I=0。然后用均值/中位数等填充 X。 | 强烈推荐。假设缺失机制是非随机的(MNAR),即缺失的原因本身带有信息。 | 捕捉了“不愿填写”或“信息不存在”本身所包含的信号,保留了原始数据结构。 |
| 8. 特殊模型 | 使用能够自动处理缺失值的模型,例如基于树的模型(如 XGBoost, LightGBM, CatBoost)。 | 当缺失模式复杂、缺失量较大时。 | 模型在节点划分时可以自动处理或学习缺失值,无需手动填充。 |
3.4案例
在婚恋相亲网站的场景中,缺失值往往不是随机的,而是带有明确的意图或隐私偏好(例如,高收入者可能不填收入,低收入者也可能不填收入)。因此,推荐结合使用以下方法:
- 指示变量 + 填充 (方法 7 + 4):
- 数值特征(如年收入、身高):用中位数填充,并新增一个“年收入_缺失指示”的二元特征。
- 类别特征(如家庭状况):用“Unknown”或“未公开”作为单独的类别进行填充。
- 使用树模型 (方法 8): 优先使用 XGBoost 或 LightGBM 等集成树模型进行预测/匹配建模,因为它们对缺失值的鲁棒性更好,并且能自动学习缺失值模式。
- 领域知识优先: 某些关键特征(如“性别”、“年龄”、“城市”)如果缺失,可能直接导致匹配失败,应要求用户必须填写,或者直接删除该记录。
4.线性回归和逻辑回归极高的耦合度
线性回归(Linear Regression)和逻辑回归(Logistic Regression)在数学和结构上确实存在着极高的耦合度。它们常常被一起教授,正是因为它们共享了“广义线性模型”的核心思想。
无论是在线性回归还是逻辑回归中,模型的第一步都是将输入特征 \(\mathbf{x}\) 进行线性组合(加权求和),得到一个预测值 \(z\):
\[z = \mathbf{W}^T \mathbf{x} + b\]两者都假设输入特征对目标变量的影响是线性的、可叠加的。—->耦合度很高。
朴素贝叶斯明确且强制地要求特征之间相互独立。这是其“朴素”的来源。
而逻辑回归(LR)则不同:
-
LR 是一种判别模型,它直接建模 $$P(y \mathbf{x})\(,并不对输入特征\)\mathbf{x}\(的**联合概率分布**\)P(x_1, x_2, \dots, x_n)$$ 做任何假设。 - 因此,LR 本身并没有假设特征独立性。它只关心 \(\mathbf{W}^T \mathbf{x}\) 这个线性组合,模型参数 $\mathbf{W}$ 会自动学习特征之间的相关性。
LR 的耦合在于它强制将特征的贡献以线性和叠加的方式聚合,这限制了它无法捕捉特征之间的复杂非线性交互作用。
另外,线性部分 \(\mathbf{W}^T \mathbf{x} + b\) 过于紧密地依赖于特征间的关系,从而导致: 如果 \(x_i\) 和 \(x_j\) 强相关,模型很难唯一确定它们各自的权重 \(w_i\) 和 \(w_j\),从而让模型结构变得脆弱。(解决办法:利用正则化(如 L1 或 L2)来解耦 LR 模型中特征之间的相关性,从而处理多重共线性问题)
显然,特征之间独立的可能性一般不大。所以朴素贝叶斯使用场景极其有限。
但是朴素贝叶斯对于 数据缺失,又想要数据解耦 的场景又很友好。
| 计算后验概率 $$P(y_k=1 | \mathbf{x})$$: |
从通用贝叶斯公式到朴素贝叶斯分类器的关键一步。
\[P(y_k=1|\mathbf{x}) = \frac{P(y_k=1) \cdot P(x_1|y_k=1) \cdot P(x_2|y_k=1) \cdot P(x_3|y_k=1)}{P(x_1, x_2, x_3)}\]| 这个推导的关键在于分子中对**似然项 $$P(\mathbf{x} | y_k=1)$$ 的分解**: |
根据朴素贝叶斯的核心假设(朴素假设):在类别 \(y\) 确定的条件下,所有特征 \(x_i\) 之间相互独立。
因此,联合条件概率可以分解为各个特征条件概率的乘积:
\[P(x_1, x_2, x_3 | y_k=1) \approx P(x_1|y_k=1) \cdot P(x_2|y_k=1) \cdot P(x_3|y_k=1)\]所以,朴素贝叶斯就是搞统计,且样本少的时候,误差就很大了,样本可能存在很强的偶然性,此时做统计就不准确了。
线性回归抗冗余强,但是朴素贝叶斯抗冗余不强。
5.拉普拉斯平滑
在朴素贝叶斯(Naive Bayes)算法中处理小样本(或零概率)问题的一种经典且有效的解决方案:拉普拉斯平滑(Laplace Smoothing)。
特征 \(x_1=1\) 的条件概率:
\[P(x_1=1 | y_1=1) = \frac{\text{Count}(x_1=1, y_1=1) + \frac{n}{2}}{\text{Count}(y_1) + n}\]特征 \(x_1=0\) 的条件概率:
\[P(x_1=0 | y_1=1) = \frac{\text{Count}(x_1=0, y_1=1) + \frac{n}{2}}{\text{Count}(y_1) + n}\]这个n的取值:根据人为干预决定。也是根据人的经验得出的。
拉普拉斯平滑通过向分子和分母添加一个虚拟计数(Pseudo-count)\(\alpha\) 来调整概率估计。
一般的拉普拉斯平滑公式如下:
\[P_{\text{smooth}}(x_i|y_k) = \frac{\text{Count}(x_i, y_k) + \alpha}{\text{Count}(y_k) + \alpha \cdot D}\]其中:
- \(\alpha\):平滑参数(通常取 1,即“加一平滑”)。
- \(D\):特征 \(x_i\) 可能的取值数量(即维度)。
它本质上是将训练集数据与一个均匀分布进行了加权平均。当样本量 \(\text{Count}(y_k)\) 很小时,添加的 \(\alpha \cdot D\) 影响较大,防止极端概率;当样本量很大时,平滑项的影响微乎其微。
通过这种方式,拉普拉斯平滑有效地解决了小样本数据中由于偶然性导致的零概率问题,使朴素贝叶斯模型在训练集不完备的情况下依然能够给出合理的概率估计。
6.信息如何量化
1.明天太阳从东边升起
2.明天下雨
显然2的信息量更大,因为1发生的概率是1,而2发生的概率显然小于1
6.1信息量 / 自信息
信息论认为,一个事件所包含的信息量与其发生的概率成反比。事件发生的概率越低,它所携带的信息量就越大。
信息论中使用对数来量化信息量 \(I(x)\),因为信息量具有可加性(独立事件的总信息量等于各自信息量之和),而概率具有可乘性(独立事件的总概率等于各自概率之积)。对数正好能将乘法转化为加法。
对于一个事件 \(x\),其自信息 \(I(x)\) 的定义为:
\[I(x) = - \log_b P(x)\]下面公式,香农严格证明过。
其中:
- \(P(x)\) 是事件 \(x\) 发生的概率。
- \(b\) 是对数的底数,它决定了信息量的单位:
- 当 \(b=2\) 时,信息量的单位是比特 (bits)。
- 当 \(b=e\) 时,信息量的单位是奈特 (nats)。
通过这个公式,可以看到:
- 如果 \(P(x) = 1\),则 \(I(x) = -\log_b(1) = 0\)。
- 如果 \(P(x) \to 0\),则 \(I(x) \to \infty\)。
这个概念是后续熵 (Entropy)、交叉熵 (Cross-Entropy) 和信息增益 (Information Gain) 等机器学习中核心概念的基石。
比如推荐系统,喜欢推荐“新奇特”的信息一样,其信息量很大,发生的概率很小。
6.2信息熵
说白了,信息熵是信息量的期望。
信息熵是用来量化一个随机变量或一个系统所包含的平均不确定性或信息量。衡量在观察到 \(X\) 的任何结果之前,我们需要多少信息才能确定其结果。
在机器学习中,熵常用于决策树(信息增益)、模型评估(交叉熵损失)等方面。
熵可以被视为随机变量 \(X\) 所有可能结果的自信息期望值。
对于一个离散随机变量 \(X\),它有 \(n\) 种可能的取值 \(\{x_1, x_2, \dots, x_n\}\),每种取值的概率是 \(P(x_i)\),其熵 \(H(X)\) 定义为:
\[H(X) = E[I(X)] = \sum_{i=1}^{n} P(x_i) \cdot I(x_i)\]将自信息 \(I(x_i) = -\log_2 P(x_i)\) 代入,得到最终的熵公式(通常以比特为单位,故取底数为 2):
\[H(X) = - \sum_{i=1}^{n} P(x_i) \log_2 P(x_i)\]单位: 比特(bits)。熵的数值代表了要对该随机变量进行编码所需的平均最小比特数。
熵值越高,不确定性越大。 样本的分布越均匀,熵越大。
熵值越低,不确定性越小。 样本的分布越集中,熵越小。
熵给出了对随机变量编码所需的理论平均最短长度。
例如,如果一个系统的信息熵是 3 比特,那么在平均意义上,你需要 3 个二元问题(是/否)才能确定该系统的状态。
熵是计算信息增益的基础。在每次分裂时,决策树选择能最大程度降低熵(即最大程度减少不确定性)的特征,从而达到最佳分类效果。
交叉熵(Cross-Entropy)和相对熵(KL 散度)都是基于信息熵的概念发展而来,用于衡量模型预测的概率分布与真实概率分布之间的差异。