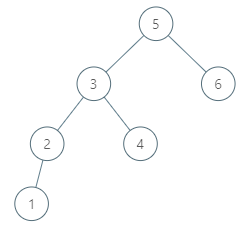
1.求所有祖先节点
先说结论:
节点 \(x\) 的所有祖先节点 = 先序遍历序列中出现在\(x\) 左边的节点集合 ∩ 后序遍历序列中出现在右边\(x\) 的节点集合。
例如求下图中x的所有祖先节点:
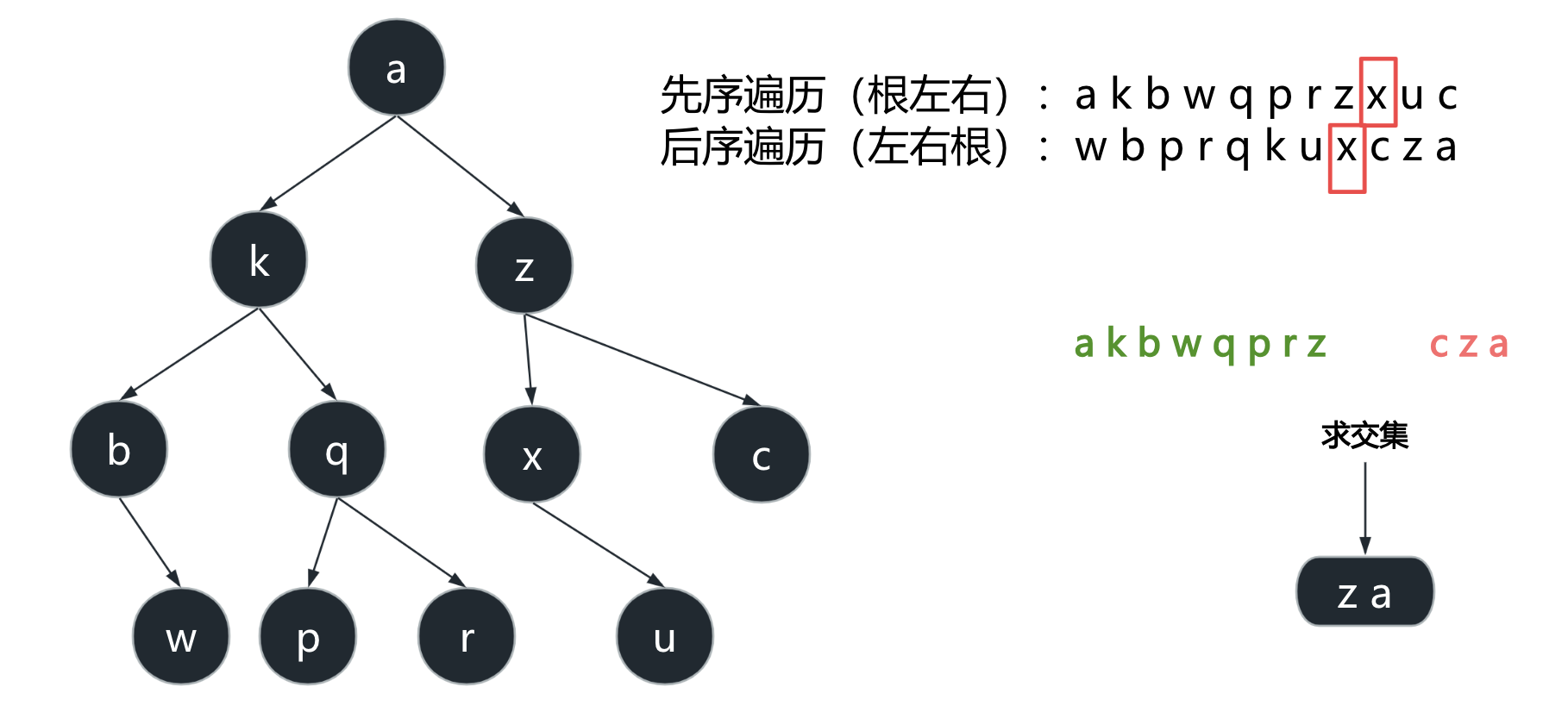
如何证明上面的结论呢?
根据先序遍历的定义(根左右),所以,x节点的祖先一定全部在先序遍历x的左边。那么后序遍历中也是同理,x的祖先一定在x后序遍历的右边。
然后证明:为什么两者的交集只有祖先节点,没有其他节点。
- 根据先序遍历和后序遍历的定义,x的孩子节点一定出现在先序遍历x的右边,x的孩子节点一定出现在后序遍历x的左边。
- 还剩下这几类节点:
- x作为左树时,右边的兄弟们(孩子也包括)。根据定义,先序遍历中,这些节点一定在先序遍历x的右边。
- x虽然是右树,但是x的父亲挂在x父亲的父亲的左边也要考虑。根据定义,后序遍历中,这些节点一定出现在后序遍历x的左边。
- 综上,先序遍历左边的节点和后序遍历右边的节点,求交集,根本不会有这上面的2类节点,所以只剩下x的祖先节点了。那么就交集,能且仅能得到x的祖先节点。
即:我们证明了:
- 祖先节点\(\in L_{pre}\) 且\(\in R_{post}\)
- 子孙节点\(\notin L_{pre}\)
- 左旁系节点\(\notin R_{post}\) 且 右旁系节点\(\notin L_{pre}\)
只有\(x\)的祖先节点才能同时满足”在先序遍历中出现在\(x\)左边”和 “在后序遍历中出现在右边\(x\)“这两 个严格的条件。因此,交集只包含且恰好包含了节点$x$的所有祖先节点。
2.层序遍历
对于下面的结构:
1
2
3
4
5
6
7
8
9
public static class Node {
public int value;
public Node left;
public Node right;
public Node(int v) {
value = v;
}
}
如果层序遍历要求只是打印,下面的解法就可以:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public static void level(Node head) {
if (head == null) {
return;
}
Queue<Node> queue = new LinkedList<>();
queue.add(head);
while (!queue.isEmpty()) {
Node cur = queue.poll();
System.out.println(cur.value);
if (cur.left != null) {
queue.add(cur.left);
}
if (cur.right != null) {
queue.add(cur.right);
}
}
}
关于层序遍历力扣上也有题目,但是返回要求是List.
2.1力扣102. 二叉树的层序遍历
要求函数签名是:
1
public List<List<Integer>> levelOrder(TreeNode root) {
解法如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> ans = new ArrayList<>();
if (root == null) {
return ans;
}
Queue<TreeNode> q = new LinkedList<>();
q.add(root);
while (!q.isEmpty()) {
int size = q.size();
List<Integer> curAns = new ArrayList<>();
for (int i = 0; i < size;i++) {
TreeNode cur = q.poll();
curAns.add(cur.val);
if (cur.left != null) {
q.add(cur.left);
}
if (cur.right != null) {
q.add(cur.right);
}
}
ans.add(curAns);
}
return ans;
}
}
2.2力扣107. 二叉树的层序遍历 II
还有一道题也类似:107. 二叉树的层序遍历 II
解法如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<List<Integer>> levelOrderBottom(TreeNode root) {
List<List<Integer>> ans = new ArrayList<>();
if (root == null) {
return ans;
}
Queue<TreeNode> q = new LinkedList<>();
q.add(root);
while (!q.isEmpty()) {
int size = q.size();
List<Integer> curAns = new ArrayList<>();
for (int i = 0;i < size;i++) {
TreeNode cur = q.poll();
curAns.add(cur.val);
if (cur.left != null) {
q.add(cur.left);
}
if (cur.right != null) {
q.add(cur.right);
}
}
ans.add(0, curAns);
}
return ans;
}
}
3.实现二叉树的序列化和反序列化
3.1先序遍历序列化
1
2
3
4
5
6
7
8
9
10
11
12
13
14
public Queue<String> preSerial(TreeNode root) {
Queue<String> ans = new LinkedList<>();
pres(root, ans);
return ans;
}
public void pres(TreeNode root, Queue<String> ans) {
if (root == null) {
ans.add(null);
} else {
ans.add(String.valueOf(root.val));
pres(root.left, ans);
pres(root.right, ans);
}
}
3.2先序遍历反序列化
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public TreeNode buildByPreList(Queue<String> preList) {
if (preList == null || preList.size() == 0) {
return null;
}
return preb(preList);
}
public TreeNode preb(Queue<String> preList) {
String value = preList.poll();
if (value == null) {
return null;
}
TreeNode head = new TreeNode(Integer.valueOf(value));
head.left = preb(preList);
head.right = preb(preList);
return head;
}
3.3中序遍历无法反序列化
反序列化,由于从中序遍历数组中无法知道根节点的位置,所以无法进行反序列化。
3.4层序遍历序列化
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public Queue<String> levelSerial(TreeNode head) {
Queue<String> ans = new LinkedList<>();
if (head == null) {
ans.add(null);
} else {
ans.add(String.valueOf(head.val));
Queue<TreeNode> nodes = new LinkedList<>();
nodes.add(head);
while (!nodes.isEmpty()) {
head = nodes.poll();
if (head.left != null) {
nodes.add(head.left);
ans.add(String.valueOf(head.left.val));
} else {
ans.add(null);
}
if (head.right != null) {
nodes.add(head.right);
ans.add(String.valueOf(head.right.val));
} else {
ans.add(null);
}
}
}
return ans;
}
3.5层序遍历反序列化
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
public TreeNode buildbyLevelQueue(Queue<String> levelList) {
if (levelList == null || levelList.size() == 0) {
return null;
}
TreeNode head = generateNode(levelList.poll());
Queue<TreeNode> queue = new LinkedList<>();
if (head != null) {
queue.add(head);
}
TreeNode node = null;
while (!queue.isEmpty()) {
node = queue.poll();
node.left = generateNode(levelList.poll());
node.right = generateNode(levelList.poll());
if (node.left != null) {
queue.add(node.left);
}
if (node.right != null) {
queue.add(node.right);
}
}
return head;
}
public TreeNode generateNode(String v) {
if (v == null) {
return null;
}
return new TreeNode(Integer.parseInt(v));
}
3.6力扣297. 二叉树的序列化与反序列化
一模一样的题牛客上还有:https://www.nowcoder.com/practice/cf7e25aa97c04cc1a68c8f040e71fb84
https://www.nowcoder.com/questionTerminal/cf7e25aa97c04cc1a68c8f040e71fb84
类似题(ACM风格):https://www.nowcoder.com/practice/d6425eab86fc402085f9fafc0db97cc2
解法1:先序遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
public class Codec {
public int cnts;
// Encodes a tree to a single string.
public String serialize(TreeNode root) {
StringBuilder ans = new StringBuilder();
pre(root, ans);
return ans.toString();
}
public void pre(TreeNode root, StringBuilder ans) {
if (root == null) {
ans.append("#,");
} else {
ans.append(root.val + ",");
pre(root.left, ans);
pre(root.right, ans);
}
}
// Decodes your encoded data to tree.
public TreeNode deserialize(String data) {
String[] str = data.split(",");
cnts = 0;
return reconPreS(str);
}
public TreeNode reconPreS(String[] str) {
String cur = str[cnts++];
if (cur.equals("#")) {
return null;
} else {
TreeNode root = new TreeNode(Integer.valueOf(cur));
root.left = reconPreS(str);
root.right = reconPreS(str);
return root;
}
}
}
// Your Codec object will be instantiated and called as such:
// Codec ser = new Codec();
// Codec deser = new Codec();
// TreeNode ans = deser.deserialize(ser.serialize(root));
解法2:层序遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
public class Codec {
public int cnts;
// Encodes a tree to a single string.
public String serialize(TreeNode root) {
StringBuilder ans = new StringBuilder();
Queue<TreeNode> q = new LinkedList<>();
if (root != null) {
ans.append(root.val + ",");
q.add(root);
while (!q.isEmpty()) {
TreeNode node = q.poll();
if (node.left != null) {
ans.append(node.left.val + ",");
q.add(node.left);
} else {
ans.append("#,");
}
if (node.right != null) {
ans.append(node.right.val + ",");
q.add(node.right);
} else {
ans.append("#,");
}
}
}
return ans.toString();
}
// Decodes your encoded data to tree.
public TreeNode deserialize(String data) {
if (data.equals("")) {
return null;
} else {
String[] str = data.split(",");
Queue<TreeNode> queue = new LinkedList<>();
TreeNode root = generateNode(str[0]);
cnts = 1;
if (root != null) {
queue.add(root);
}
while (!queue.isEmpty()) {
TreeNode node = queue.poll();
node.left = generateNode(str[cnts++]);
node.right = generateNode(str[cnts++]);
if (node.left != null) {
queue.add(node.left);
}
if (node.right != null) {
queue.add(node.right);
}
}
return root;
}
}
public TreeNode generateNode(String v) {
if (v.equals("#")) {
return null;
}
return new TreeNode(Integer.parseInt(v));
}
}
// Your Codec object will be instantiated and called as such:
// Codec ser = new Codec();
// Codec deser = new Codec();
// TreeNode ans = deser.deserialize(ser.serialize(root));
3.7牛客ACM风格-二叉树序列化
https://www.nowcoder.com/practice/cf7e25aa97c04cc1a68c8f040e71fb84
这道题与上面不同的地方在于处理输入,这里需要单独创建一个createTree方法,创建二叉树。题目给的信息是:
第一行输入两个整数 n 和 root,n 表示二叉树的总节点个数,root 表示二叉树的根节点。 以下 n 行每行三个整数 fa,lch,rch,表示 fa 的左儿子为 lch,右儿子为 rch。(如果 lch 为 0 则表示 fa 没有左儿子,rch同理)
比如下面的例子:
输入:
1
2
3
2 1
1 2 0
2 0 0
输出:
1
2
1!2!#!#!#!
1!2!#!#!#!
解法如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
import java.util.*;
import java.io.*;
class TreeNode {
int val;
TreeNode left;
TreeNode right;
public TreeNode(int v) {
val = v;
left = null;
right = null;
}
}
// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StreamTokenizer in = new StreamTokenizer(br);
PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
TreeNode root = createTreeNode(in);
// (先序)序列化这棵树
String ans1 = preSerial(root);
String ans2 = levelSerial(root);
out.println(ans1);
out.println(ans2);
out.flush();
br.close();
out.close();
}
public static TreeNode createTreeNode(StreamTokenizer in) throws IOException {
if (in.nextToken() == StreamTokenizer.TT_EOF) return null;
int n = (int)in.nval;// 节点个数
in.nextToken();
HashMap<Integer, TreeNode> map = new HashMap<>();
int rootVal = (int)in.nval;
TreeNode root = new TreeNode(rootVal);
map.put(rootVal, root);
in.nextToken();
for (int i = 0;i < n;i++) {
int rootV = (int)in.nval;
in.nextToken();
TreeNode r = map.get(rootV);
if (r == null) break;
int leftV = (int)in.nval;
in.nextToken();
if (leftV != 0) {
TreeNode l = new TreeNode(leftV);
map.put(leftV, l);
r.left = l;
}
int rightV = (int)in.nval;
in.nextToken();
if (rightV != 0) {
TreeNode ri = new TreeNode(rightV);
map.put(rightV, ri);
r.right = ri;
}
}
return map.get(rootVal);
}
public static String preSerial(TreeNode root) {
StringBuilder ans = new StringBuilder();
f(root, ans);
return ans.toString();
}
public static void f(TreeNode root, StringBuilder ans) {
if (root == null) {
ans.append("#!");
return;
}
ans.append(root.val + "!");
f(root.left, ans);
f(root.right, ans);
}
public static String levelSerial(TreeNode root) {
StringBuilder ans = new StringBuilder();
if (root == null) {
ans.append("#!");
} else {
Queue<TreeNode> q = new LinkedList<>();
q.add(root);
ans.append(root.val + "!");
while (!q.isEmpty()) {
TreeNode cur = q.poll();
if (cur.left != null) {
ans.append(cur.left.val + "!");
q.add(cur.left);
} else {
ans.append("#!");
}
if (cur.right != null) {
ans.append(cur.right.val + "!");
q.add(cur.right);
} else {
ans.append("#!");
}
}
}
return ans.toString();
}
}
4.力扣431多叉树编码为二叉树
同样的题还有:https://www.naukri.com/code360/problems/encode-n-ary-tree-to-binary-tree_1281859?leftPanelTabValue=PROBLEM
核心思想:对于节点x的孩子,都放在左树的右边界上。比如:

变成二叉树就是

上图中,A的孩子有3个:B,C,D,变成二叉树之后这3个节点都在A左树的右边界上了,其他节点同理。
解法:
1.时间复杂度
在整个编码和解码过程中,算法的递归(或迭代)遍历了N叉树\(T_{N}\) 中的每一个节点恰好一次。在 每个节点上,操作(创建新节点、赋值)都是$O(1)$ 的。
总时间复杂度:\(O(n)\),其中$n$是 N 叉树中的节点总数。
2.空间复杂度
空间复杂度主要由新创建的节点和递归调用栈的深度决定。
- 新创建的节点: 编码过程创建了 \(n\) 个新的 TreeNode 节点。解码过程创建了 \(n\)个新的 Node 节点,以及用于存储子节点的
List<Node>列表。所需的空间与节点总数成正比。 - 节点空间: \(O(n)\)
递归调用栈:
- 编码: 递归发生在 en 方法中对 cur.left 的赋值,这对应于 N 叉树中的 深度。因此,递归栈深度等于 N 叉树的深度 \(h\)。
- 解码: 递归发生在 de 方法中对 root.left 的调用,这也对应于 N 叉树的 深度 \(h\)。
- 栈空间: \(O(h)\),其中 是\(h\) N 叉树的最大深度(树的高度)。在最坏情况下(树退化成链表),可以\(h\)达到 $n$,因此最坏情况下的栈空间是 。\(O(n)\)
总空间复杂度: \(O(n)\) (考虑新创建的节点和最坏情况下的递归栈深度)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
/*
// Definition for a Node.
class Node {
public int val;
public List<Node> children;
public Node() {}
public Node(int _val) {
val = _val;
}
public Node(int _val, List<Node> _children) {
val = _val;
children = _children;
}
};
*/
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Codec {
// Encodes an n-ary tree to a binary tree.
public TreeNode encode(Node root) {
if (root == null) {
return null;
}
TreeNode head = new TreeNode(root.val);
head.left = en(root.children);
return head;
}
public TreeNode en(List<Node> children) {
TreeNode head = null, cur = null;
for (Node child : children) {
TreeNode t = new TreeNode(child.val);
if (head == null) {
head = t;
} else {
cur.right = t;
}
cur = t;
cur.left = en(child.children);
}
return head;
}
// Decodes your binary tree to an n-ary tree.
public Node decode(TreeNode root) {
if (root == null) {
return null;
}
return new Node(root.val, de(root.left));
}
public List<Node> de(TreeNode root) {
List<Node> children = new ArrayList<>();
while (root != null) {
Node cur = new Node(root.val, de(root.left));
children.add(cur);
root = root.right;
}
return children;
}
}
// Your Codec object will be instantiated and called as such:
// Codec codec = new Codec();
// codec.decode(codec.encode(root));
https://www.naukri.com/code360/problems/encode-n-ary-tree-to-binary-tree_1281859?leftPanelTabValue=PROBLEM
这个网站的解法有点不同,因为数据结构加上了泛型
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
import java.util.* ;
import java.io.*;
/*************************************************************
Binary tree node class for reference:
class BTreeNode<T> {
public T data;
public BTreeNode<T> left;
public BTreeNode<T> right;
BTreeNode(T data) {
this.data = data;
left = null;
right = null;
}
}
Nary tree node class for reference:
class NTreeNode<T> {
public T data;
public ArrayList<NTreeNode<T>> child;
NTreeNode(T data) {
this.data = data;
child = new ArrayList();
}
}
*************************************************************/
public class Solution {
public static BTreeNode<Integer> encode(NTreeNode<Integer> root) {
if (root == null) return null;
BTreeNode head = new BTreeNode(root.data);
head.left = en(root.child);
return head;
}
public static BTreeNode<Integer> en(ArrayList<NTreeNode<Integer>> child) {
BTreeNode head = null, cur = null;
for (NTreeNode n : child) {
BTreeNode tNode = new BTreeNode(n.data);
if (head == null) {
head = tNode;
} else {
cur.right = tNode;
}
cur = tNode;
cur.left = en(n.child);
}
return head;
}
public static NTreeNode<Integer> decode(BTreeNode<Integer> root) {
if (root == null) {
return null;
}
NTreeNode ans = new NTreeNode(root.data);
ans.child = de(root.left);
return ans;
}
public static ArrayList<NTreeNode> de(BTreeNode root ) {
ArrayList<NTreeNode> children = new ArrayList<>();
while (root != null) {
NTreeNode cur = new NTreeNode(root.data);
cur.child = de(root.left);
children.add(cur);
root = root.right;
}
return children;
}
}
5.打印整棵树的打印函数
如何设计一个打印整棵树的打印函数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
public static void printTree(Node head) {
System.out.println("Binary Tree:");
printInOrder(head, 0, "H", 17);
System.out.println();
}
public static void printInOrder(Node head, int height, String to, int len) {
if (head == null) {
return;
}
printInOrder(head.right, height + 1, "v", len);
String val = to + head.value + to;
int lenM = val.length();
int lenL = (len - lenM) / 2;
int lenR = len - lenM - lenL;
val = getSpace(lenL) + val + getSpace(lenR);
System.out.println(getSpace(height * len) + val);
printInOrder(head.left, height + 1, "^", len);
}
public static String getSpace(int num) {
String space = " ";
StringBuffer buf = new StringBuffer("");
for (int i = 0; i < num; i++) {
buf.append(space);
}
return buf.toString();
}
6.二叉树最宽的层有多少个节点
6.2不计空节点
求二叉树最宽的层有多少个节点,不计空节点。
其实就是层序遍历。
测试链接:https://www.naukri.com/code360/problems/maximum-width-of-a-binary-tree_981173?leftPanelTabValue=PROBLEM
https://www.naukri.com/code360/problems/maximum-width-in-binary-tree_763671?leftPanelTabValue=PROBLEM
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public static int levelOrder(Node head) {
if (head == null) return 0;
Queue<Node> queue = new LinkedList<>();
queue.add(head);
int ans = 0;
while (!queue.isEmpty()) {
int size = queue.size();
ans = Math.max(ans, size);
for (int i = 0;i < size;i++) {
Node cur = queue.poll();
if (cur.left != null) {
queue.add(cur.left);
}
if (cur.right != null) {
queue.add(cur.right);
}
}
}
return ans;
}
6.2计空节点-力扣662
https://leetcode.cn/problems/maximum-width-of-binary-tree/description/
复杂度类型 结果 描述
时间复杂度 $O( N)$ $N$为树中节点总数,因为每个节点只访问一次。 空间复杂度 $O( W)$ $W$ 为树的最大宽度,由队列存储的当前层节点数决定。最环情况下$W\approx N$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public class QueueNode {
TreeNode root;
long index;
QueueNode(TreeNode root, long index) {
this.root = root;
this.index = index;
}
}
public int widthOfBinaryTree(TreeNode root) {
if (root == null) {
return 0;
}
int ans = 1;
Queue<QueueNode> queue = new LinkedList<>();
queue.add(new QueueNode(root, ans));
while(!queue.isEmpty()) {
int size = queue.size();
long first = 0;
long last = 0;
for(int i = 0; i < size; i++) {
QueueNode poll = queue.poll();
long index = poll.index;
if(i == 0) {
// 当前层第一个出队的节点(最左侧节点)
first = index;
// 注意这里
last = index;
} else if (i == size - 1 ){
// 当前层最后一个出队的节点(最右侧节点)
last = index;
}
TreeNode left = poll.root.left;
TreeNode right = poll.root.right;
if(left != null) {
queue.add(new QueueNode(left, index * 2));
}
if(right != null) {
queue.add(new QueueNode(right, index * 2 + 1));
}
}
ans = (int) Math.max(ans, last - first + 1);
}
return ans;
}
}
7.二叉树节点最大高度
测试链接:
https://www.naukri.com/code360/problems/maximum-depth-of-a-binary-tree_1090542?leftPanelTabValue=PROBLEM
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import java.util.* ;
import java.io.*;
/****************************************************
class BinaryTreeNode<T> {
T data;
BinaryTreeNode<T> left;
BinaryTreeNode<T> right;
public BinaryTreeNode(T data) {
this.data = data;
}
}
*****************************************************/
public class Solution
{
public static int findMaxDepth(BinaryTreeNode<Integer> root)
{
if (root == null) return 0;
return (Math.max(findMaxDepth(root.left),findMaxDepth(root.right))) + 1;
}
}
下面这道题,貌似不算头节点的高度:https://www.hackerrank.com/challenges/three-month-preparation-kit-tree-height-of-a-binary-tree/problem
1
2
3
4
5
6
7
8
public static int height(Node root) {
return f(root)-1;
}
public static int f(Node root) {
if (root == null) return 0;
return (Math.max(f(root.left), f(root.right))) + 1 ;
}
8.找后继节点(有parent指针)
测试链接:510. 二叉搜索树中的中序后继 II
题意描述:
二叉树结构如下定义:
1
2
3
4
5
6
class Node {
public int val;
public Node left;
public Node right;
public Node parent;
};
给你二叉树中的某个节点,返回该节点的后继节点
首先关于后继节点,定义如下:
在一个二叉搜索树(BST)中,一个给定节点 X 的后继节点是指:
在中序遍历(In-order Traversal)的序列中,紧随节点 X 之后的那个节点。
或者用值的关系来描述:
后继节点是所有键值(key/value)大于节点 X 的节点中,键值最小的那一个节点。
比如下面这棵树:
中序遍历是1,2,3,4,5,6
节点6的后继是null
这颗树的中序遍历是1,2,3,所以节点1的后继是2
如果给的是头节点,那么求个中序遍历就可以了,然后找出中序遍历中的下一个。此时的时间复杂度是\(O(N)\)
现在题目还增加了一个指针,某个节点不仅有left和right,还有parent指针。
那么现在能不能比\(O(N)\)更强,使得时间复杂度是\(O(k)\),\(k\)是某个节点到其后继的真实距离呢?
8.1思路
情况1:节点有右孩子,直接返回右树上最左的孩子
情况2:如下图所示,但是如果一直往上找,没有这个位置,那么就是null。

没有后继的情况:

情况3:

8.2解法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public Node inorderSuccessor(Node node) {
if (node == null) return null;
if (node.right != null) {
return getMostLeft(node.right);
}
Node parent = node.parent;
while (parent != null && parent.right == node) {
node = parent;
parent = node.parent;
}
return parent;
}
public Node getMostLeft(Node root) {
if (root == null) {
return root;
}
while (root.left != null) {
root = root.left;
}
return root;
}
}
9.找二叉搜索树后继节点
测试链接:
https://leetcode.cn/problems/inorder-successor-in-bst/description/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public TreeNode inorderSuccessor(TreeNode root, TreeNode p) {
if (root == null ) return null;
if (root.val <= p.val) {
return inorderSuccessor(root.right, p);
}
TreeNode left = inorderSuccessor(root.left, p);
return left == null ? root : left;
}
}
10.二叉树折纸问题
【微软面试题】
测试链接:(需IDE中自己测试)https://kirsten-1.github.io/2025/10/02/%E7%AE%97%E6%B3%95%E9%A2%98%E5%BA%93-2%E6%8A%98%E7%BA%B8%E9%97%AE%E9%A2%98/
请把一段纸条竖着放在桌子上,然后从纸条的下边向上方对折1次,压出折痕后展开。此时折痕是凹下去的,即折痕突起的方向指向纸条的背面。 如果从纸条的下边向上方连续对折2次,压出折痕后展开,此时有三条折痕,从上到下依次是下折痕、下折痕和上折痕。
给定一个输入参数N,代表纸条都从下边向上方连续对折N次。 请从上到下打印所有折痕的方向。 例如:N=1时,打印: down N=2时,打印: down down up
本题主要是发现整个过程的规律,假设中间分割线看成是一个二叉树的头结点,分割线的上方看成是左子树,分割线的下方看成是右子树,则有如下规律
- 头是凹折痕
- 左子树的头节点都是凹折痕
- 右子树的头节点都是凸折痕
打印的就是中序遍历
解法如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public static List<String> ans ;
public static List<String> printAllFolds(int N) {
ans = new ArrayList<>();
if (N == 0) return ans;
process(1,N, true);
return ans;
}
public static void process(int i, int N, boolean down) {
if (i > N) return;
process(i + 1, N, true);
ans.add(down ? "凹" : "凸");
process(i + 1, N, false);
}
11.判断是否是完全二叉树
给你一棵二叉树的根节点 root ,请你判断这棵树是否是一棵 完全二叉树 。
在一棵 完全二叉树 中,除了最后一层外,所有层都被完全填满,并且最后一层中的所有节点都尽可能靠左。最后一层(第 h 层)中可以包含 1 到\(2^h\) 个节点。
说白了,完全二叉树就是:满的或者是在变满的路上。
本题测试链接:958. 二叉树的完全性检验
11.1二叉树的递归套路
可以解决面试中绝大多数的二叉树问题尤其是树型dp问题
本质是利用递归遍历二叉树的便利性
1)假设以X节点为头,假设可以向X左树和X右树要任何信息 2)在上一步的假设下,讨论以X为头节点的树,得到答案的可能性(最重要) 3)列出所有可能性后,确定到底需要向左树和右树要什么样的信息 4)把左树信息和右树信息求全集,就是任何一棵子树都需要返回的信息S 5)递归函数都返回S,每一棵子树都这么要求 6)写代码,在代码中考虑如何把左树的信息和右树信息整合出整棵树的信息
11.2力扣958二叉树的完全性检验(非递归)
思路:
- 如果一个节点,只有右孩子没有左孩子,直接返回
false - 依次按层遍历每个节点,一开始遇到的一定是同时有左孩子也有右孩子的节点,然后遇到的第一个叶节点(没有左孩子也没有右孩子)或者只有左孩子的节点之后,后面所有节点一定是叶节点。
- 另外,空树一般算完全二叉树,但是最好也看下题意的描述。
解法如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean isCompleteTree(TreeNode root) {
if (root == null) return true;
Queue<TreeNode> q = new LinkedList<>();
q.add(root);
boolean leaf = false;
TreeNode l = null;
TreeNode r = null;
while (!q.isEmpty()) {
TreeNode cur = q.poll();
l = cur.left;
r = cur.right;
if ((leaf && ((l != null) || (r != null))) || (l == null && r != null)) {
return false;
}
if (l != null) {
q.add(l);
}
if (r != null) {
q.add(r);
}
if (l == null || r == null) {
leaf = true;
}
}
return true;
}
}
11.3递归写法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
import java.util.*;
/*
* public class TreeNode {
* int val = 0;
* TreeNode left = null;
* TreeNode right = null;
* public TreeNode(int val) {
* this.val = val;
* }
* }
*/
class Info {
boolean isFull;
boolean isCBT;
int height;
public Info (boolean full, boolean cbt, int h) {
isFull = full;
isCBT = cbt;
height = h;
}
}
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param root TreeNode类
* @return bool布尔型
*/
public boolean isCompleteTree (TreeNode root) {
return process(root).isCBT;
}
public Info process(TreeNode root) {
if (root == null) {
return new Info(true, true, 0);
}
Info leftInfo = process(root.left);
Info rightInfo = process(root.right);
int height = Math.max(leftInfo.height, rightInfo.height) + 1;
boolean isFull = leftInfo.isFull && rightInfo.isFull && leftInfo.height == rightInfo.height;
boolean isCBT = false;
if (isFull) {
isCBT = true;
} else if (leftInfo.isFull && rightInfo.isCBT && leftInfo.height == rightInfo.height) {
isCBT = true;
} else if (leftInfo.isFull && rightInfo.isFull && (leftInfo.height == (rightInfo.height + 1))) {
isCBT = true;
} else if (leftInfo.isCBT && rightInfo.isFull && (leftInfo.height == (rightInfo.height + 1))) {
isCBT = true;
}
return new Info(isFull, isCBT, height);
}
}
12.判断是否是平衡二叉树
给定一棵二叉树的头节点head,返回这颗二叉树是不是平衡二叉树
测试链接:110. 平衡二叉树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
class Info {
boolean isB;
int height;
public Info(boolean is, int h) {
isB = is;
height = h;
}
}
public boolean isBalanced(TreeNode root) {
return isBB(root).isB;
}
public Info isBB(TreeNode root) {
if (root == null) {
return new Info(true, 0);
}
Info leftInfo = isBB(root.left);
Info rightInfo = isBB(root.right);
int height = Math.max(leftInfo.height, rightInfo.height) + 1;
boolean is = leftInfo.isB && rightInfo.isB && (Math.abs(leftInfo.height - rightInfo.height)<2);
return new Info(is, height);
}
}
13.是否是搜索二叉树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
class Info {
boolean isBST;
int min;
int max;
public Info(boolean is, int mi, int ma) {
isBST = is;
min = mi;
max = ma;
}
}
public boolean isValidBST(TreeNode root) {
return process(root).isBST;
}
public Info process(TreeNode root) {
if (root == null) {
return null;
}
Info leftInfo = process(root.left);
Info rightInfo = process(root.right);
int min = root.val;
int max = root.val;
if (leftInfo != null) {
min = Math.min(min, leftInfo.min);
max = Math.max(max, leftInfo.max);
}
if (rightInfo != null) {
min = Math.min(min, rightInfo.min);
max = Math.max(max, rightInfo.max);
}
boolean isLeftBST = leftInfo == null ? true : leftInfo.isBST;
boolean isRightBST = rightInfo == null ? true : rightInfo.isBST;
boolean isLessLeft = leftInfo == null ? true : (leftInfo.max < root.val);
boolean isBiggerRight = rightInfo == null ? true : (rightInfo.min > root.val);
boolean is = isLeftBST && isRightBST && isLessLeft && isBiggerRight;
return new Info(is, min, max);
}
}
14.整棵二叉树的最大距离(二叉树的直径)
给定一棵二叉树的头节点head,任何两个节点之间都存在距离, 返回整棵二叉树的最大距离
链接:543. 二叉树的直径
【思路】
- X左树的最大距离
- X右树的最大距离
- X左树与X最远+X右树与X最远+1
其中X左树与X最远与X左树高度有关!
解法:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
class Info {
int maxDistance;
int height ;
public Info(int m, int h) {
maxDistance = m;
height = h;
}
}
public int diameterOfBinaryTree(TreeNode root) {
return process(root).maxDistance;
}
public Info process(TreeNode root) {
if (root == null) {
return new Info(0, 0);
}
Info leftInfo = process(root.left);
Info rightInfo = process(root.right);
int height = (Math.max(leftInfo.height, rightInfo.height)) + 1;
int d1 = leftInfo.maxDistance;
int d2 = rightInfo.maxDistance;
int d3 = leftInfo.height + rightInfo.height;
return new Info(Math.max(d1, Math.max(d2, d3)), height);
}
}
15.是不是完美二叉树
注意区分满二叉树,完全二叉树和完美二叉树
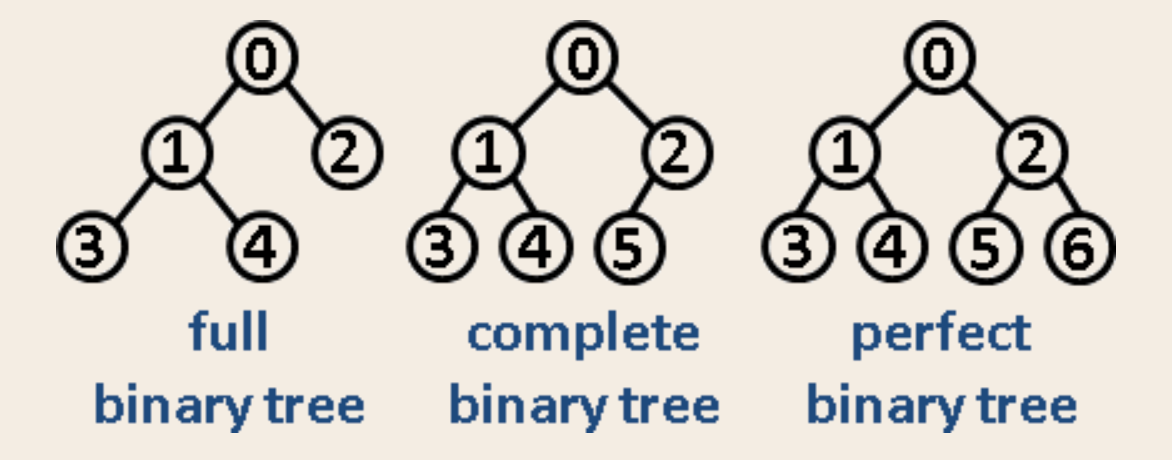
注意:满二叉树中,一个节点不是叶子节点就是有2个孩子的节点。而完全二叉树是永远在变成完美二叉树的路上。完美二叉树一定满足\(2^h-1=n\),其中\(h\)是树的高度,\(n\)是整棵树的节点的个数。
测试链接:https://www.geeksforgeeks.org/problems/perfect-binary-tree/1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
/*
class Node {
int data;
Node left, right;
public Node(int data){
this.data = data;
}
}
*/
class Solution {
class Info {
int allNodes;
int height;
public Info (int all, int h) {
allNodes = all;
height = h;
}
}
// Return True if the given Binary Tree is a Full Binary Tree. Else return False
public boolean isPerfect(Node node) {
if (node == null) return true;
Info rInfo = process(node);
return (1 << rInfo.height) - 1 == rInfo.allNodes;
}
Info process(Node node) {
if (node == null) {
return new Info(0, 0);
}
Info leftInfo = process(node.left);
Info rightInfo = process(node.right);
int height = Math.max(leftInfo.height, rightInfo.height) + 1;
int n = leftInfo.allNodes + rightInfo.allNodes + 1;
return new Info(n, height);
}
}
16.是不是满二叉树
https://www.geeksforgeeks.org/problems/full-binary-tree/1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/*Complete the function below
Node is as follows:
class Node
{
int data;
Node left, right;
Node(int item)
{
data = item;
left = right = null;
}
}
*/
class GfG {
// Return True if the given Binary Tree is a Full Binary Tree. Else return False
boolean isFullTree(Node node) {
if (node == null) return true;
if (node.left == null ^ node.right == null ) {
return false;
}
if (node.left == null && node.right == null ) {
return true;
}
return isFullTree(node.left) && isFullTree(node.right);
}
}
17.最大二叉搜索子树的大小
测试链接:https://leetcode.cn/problems/largest-bst-subtree/description/
ACM风格请练习:https://www.nowcoder.com/questionTerminal/380d49d7f99242709ab4b91c36bf2acc
给定一棵二叉树的头节点head, 返回这颗二叉树中最大的二叉搜索子树的大小
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
class Info {
int maxBSTSize;
int allSize;
int min;
int max;
public Info (int maBST, int all, int mi, int ma) {
maxBSTSize = maBST;
allSize = all;
min = mi;
max = ma;
}
}
public int largestBSTSubtree(TreeNode root) {
if (root == null) {
return 0;
}
return process(root).maxBSTSize;
}
public Info process(TreeNode root) {
if (root == null) {
return null;
}
int min = root.val;
int max = root.val;
int allSize = 1;
Info leftInfo = process(root.left);
Info rightInfo = process(root.right);
if (leftInfo != null) {
min = Math.min(min, leftInfo.min);
max = Math.max(max, leftInfo.max);
allSize += leftInfo.allSize;
}
if (rightInfo != null) {
min = Math.min(min, rightInfo.min);
max = Math.max(max, rightInfo.max);
allSize += rightInfo.allSize;
}
int p1 = leftInfo == null ? -1 : leftInfo.maxBSTSize;
int p2 = rightInfo == null ? -1 : rightInfo.maxBSTSize;
boolean isLeftBST = leftInfo == null ? true : (leftInfo.allSize ==leftInfo.maxBSTSize);
boolean isRightBST = rightInfo == null ? true : (rightInfo.allSize == rightInfo.maxBSTSize);
int p3 = -1;
if (isLeftBST && isRightBST) {
boolean isLess = leftInfo == null ? true : (leftInfo.max < root.val);
boolean isBigger = rightInfo == null ? true : (rightInfo.min > root.val);
if (isLess && isBigger) {
int leftBSTSize = leftInfo == null ? 0 : leftInfo.maxBSTSize;
int rightBSTSize = rightInfo == null ? 0 : rightInfo.maxBSTSize;
p3 = leftBSTSize + rightBSTSize + 1;
}
}
return new Info(Math.max(p1, Math.max(p2, p3)), allSize, min, max);
}
}
ACM风格:https://www.nowcoder.com/questionTerminal/380d49d7f99242709ab4b91c36bf2acc
输入是:
1
2
3
4
3 2
2 1 3
1 0 0
3 0 0
需要自己创建一颗树。
完整的解法如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
import java.util.*;
import java.io.*;
// 注意类名必须为 Main, 不要有任何 package xxx 信息
class Node {
int val;
Node left;
Node right;
public Node(int v) {
val = v;
left = null;
right = null;
}
}
class Info {
int maxBSTSize;
int allSize;
int min;
int max;
public Info(int bst, int all, int mi, int ma) {
maxBSTSize = bst;
allSize = all;
min = mi;
max = ma;
}
}
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StreamTokenizer in = new StreamTokenizer(br);
PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
while (in.nextToken() != StreamTokenizer.TT_EOF) {
Node root = createTree(in);
int ans = getMaxSubBSTNum(root);
out.println(ans);
}
out.flush();
br.close();
out.close();
}
public static int getMaxSubBSTNum(Node root) {
if (root == null) {
return 0;
}
return proecess(root).maxBSTSize;
}
public static Info proecess(Node root) {
if (root == null) {
return null;
}
Info leftInfo = proecess(root.left);
Info rightInfo = proecess(root.right);
int allSize = 1;
int min = root.val;
int max = root.val;
if (leftInfo != null) {
min = Math.min(leftInfo.min, min);
max = Math.max(leftInfo.max, max);
allSize = leftInfo.allSize + allSize;
}
if (rightInfo != null) {
min = Math.min(rightInfo.min, min);
max = Math.max(rightInfo.max, max);
allSize = rightInfo.allSize + allSize;
}
int p1 = leftInfo == null ? -1 : leftInfo.maxBSTSize;
int p2 = rightInfo == null ? -1 : rightInfo.maxBSTSize;
boolean isLeftBST = leftInfo == null ? true : (leftInfo.maxBSTSize ==
leftInfo.allSize);
boolean isRightBST = rightInfo == null ? true : (rightInfo.maxBSTSize ==
rightInfo.allSize);
int p3 = -1;
if (isLeftBST && isRightBST) {
boolean isLess = leftInfo == null ? true : (leftInfo.max < root.val);
boolean isBigger = rightInfo == null ? true : (rightInfo.min > root.val);
if (isLess && isBigger) {
int leftSize = leftInfo == null ? 0 : leftInfo.maxBSTSize;
int rightSize = rightInfo == null ? 0 : rightInfo.maxBSTSize;
p3 = leftSize + rightSize + 1;
}
}
return new Info(Math.max(p1, Math.max(p2, p3)), allSize, min, max);
}
public static Node createTree(StreamTokenizer in) throws IOException {
int n = (int)in.nval;
in.nextToken();
int rootVal = (int)in.nval;
in.nextToken();
Node root = new Node(rootVal);
HashMap<Integer, Node> map = new HashMap<>();
map.put(rootVal, root);
for (int i = 0; i < n; i++) {
int headVal = (int)in.nval;
in.nextToken();
Node head = map.get(headVal);
int leftVal = (int)in.nval;
in.nextToken();
if (leftVal != 0) {
Node leftNode = new Node(leftVal);
head.left = leftNode;
map.put(leftVal, leftNode);
}
int rightVal = (int)in.nval;
in.nextToken();
if (rightVal != 0) {
Node rightNode = new Node(rightVal);
head.right = rightNode;
map.put(rightVal, rightNode);
}
}
return root;
}
}
18.最大二叉搜索子树的头节点
解法的思路是自底向上地整合信息,对于任意节点 X,它的 Info 是根据其左右子节点 L 和 R 的 Info 计算出来的,主要考虑两种可能性来确定最大 BST:
1.继承左右子树结果(情况一):
最大的 BST 不以 X 为头。此时 X 的 maxSubBSTSize 简单地继承左子树或右子树中最大的那个 BST 尺寸,并记录相应的头节点。同时,计算出以 X 为根的整个子树的真实最小值和最大值(用于传递给 X 的父节点)。
2.X 成为新的头节点(情况二):
最大的 BST 以 X 为头。这要求 X 必须满足两个条件:
- 左子树必须整体是一个 BST,且左子树的最大值 (L.max) 小于 X.value。
- 右子树必须整体是一个 BST,且右子树的最小值 (R.min) 大于 X.value。
如果满足这些条件,那么以 X 为头的 BST 尺寸就是左子树 BST 尺寸 + 右子树 BST 尺寸 + 1。
最终,节点 X 返回的 maxSubBSTSize 是情况一和情况二中较大的那个值。通过这种递归方式,当根节点 head 的 process 调用返回时,其中 maxSubBSTHead 即为整个树中最大 BST 的头节点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
public static class Info {
public Node maxSubBSTHead;
public int maxSubBSTSize;
public int min;
public int max;
public Info(Node h, int size, int mi, int ma) {
maxSubBSTHead = h;
maxSubBSTSize = size;
min = mi;
max = ma;
}
}
public static Info process(Node X) {
if (X == null) {
return null;
}
Info leftInfo = process(X.left);
Info rightInfo = process(X.right);
int min = X.value;
int max = X.value;
Node maxSubBSTHead = null;
int maxSubBSTSize = 0;
if (leftInfo != null) {
min = Math.min(min, leftInfo.min);
max = Math.max(max, leftInfo.max);
maxSubBSTHead = leftInfo.maxSubBSTHead;
maxSubBSTSize = leftInfo.maxSubBSTSize;
}
if (rightInfo != null) {
min = Math.min(min, rightInfo.min);
max = Math.max(max, rightInfo.max);
if (rightInfo.maxSubBSTSize > maxSubBSTSize) {
maxSubBSTHead = rightInfo.maxSubBSTHead;
maxSubBSTSize = rightInfo.maxSubBSTSize;
}
}
if ((leftInfo == null ? true : (leftInfo.maxSubBSTHead == X.left && leftInfo.max < X.value))
&& (rightInfo == null ? true : (rightInfo.maxSubBSTHead == X.right && rightInfo.min > X.value))) {
maxSubBSTHead = X;
maxSubBSTSize = (leftInfo == null ? 0 : leftInfo.maxSubBSTSize)
+ (rightInfo == null ? 0 : rightInfo.maxSubBSTSize) + 1;
}
return new Info(maxSubBSTHead, maxSubBSTSize, min, max);
}
19.二叉树的最近公共祖先
这道题也可以用二叉树递归套路解题。时间复杂度是\(O(N)\),因为用的就是二叉树后序遍历。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
class Info {
boolean findA;
boolean findB;
TreeNode ans;
public Info (boolean fa, boolean fb, TreeNode an) {
findA = fa;
findB = fb;
ans = an;
}
}
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
return process(root, p, q).ans;
}
public Info process(TreeNode x, TreeNode a, TreeNode b) {
if (x == null) {
return new Info(false, false, null);
}
Info leftInfo = process(x.left, a, b);
Info rightInfo = process(x.right, a, b);
boolean findA = leftInfo.findA || rightInfo.findA || x == a;
boolean findB = leftInfo.findB || rightInfo.findB || x == b;
TreeNode ans = null;
if (leftInfo.ans != null) {
ans = leftInfo.ans;
} else if (rightInfo.ans != null) {
ans = rightInfo.ans;
} else {
if (findA && findB) {
ans = x;
}
}
return new Info(findA, findB, ans);
}
}
20.派对的最大快乐值
这道题的类似题有:力扣337. 打家劫舍 III https://leetcode.cn/problems/house-robber-iii/description/
题意描述如下:
员工信息的定义如下:
1
2
3
4
5
6
7
8
9
10
public static class Employee {
public int happy;// happy值
public List<Employee> nexts;// 所有下级(直接下级)
public Employee(int h) {
happy = h;
nexts = new ArrayList<>();
}
}
公司的每个员工都符合 Employee 类的描述。整个公司的人员结构可以看作是一棵标准的、 没有环的多叉树。树的头节点是公司唯一的老板。除老板之外的每个员工都有唯一的直接上级。 叶节点是没有任何下属的基层员工(subordinates列表为空),除基层员工外,每个员工都有一个或多个直接下级。
这个公司现在要办party,你可以决定哪些员工来,哪些员工不来,规则: 1.如果某个员工来了,那么这个员工的所有直接下级都不能来 2.派对的整体快乐值是所有到场员工快乐值的累加 3.你的目标是让派对的整体快乐值尽量大 给定一棵多叉树的头节点boss,请返回派对的最大快乐值。
利用二叉树递归套路的解法:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
public static int maxHappy2(Employee head) {
Info allInfo = process(head);
return Math.max(allInfo.no, allInfo.yes);
}
public static class Info {
public int no;
public int yes;
public Info(int n, int y) {
no = n;
yes = y;
}
}
public static Info process(Employee x) {
if (x == null) {
return new Info(0, 0);
}
int no = 0;
int yes = x.happy;
for (Employee next : x.nexts) {
Info nextInfo = process(next);
no += Math.max(nextInfo.no, nextInfo.yes);
yes += nextInfo.no;
}
return new Info(no, yes);
}
对数器如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
public static int maxHappy1(Employee boss) {
if (boss == null) {
return 0;
}
return process1(boss, false);
}
// 当前来到的节点叫cur,
// up表示cur的上级是否来,
// 该函数含义:
// 如果up为true,表示在cur上级已经确定来,的情况下,cur整棵树能够提供最大的快乐值是多少?
// 如果up为false,表示在cur上级已经确定不来,的情况下,cur整棵树能够提供最大的快乐值是多少?
public static int process1(Employee cur, boolean up) {
if (up) { // 如果cur的上级来的话,cur没得选,只能不来
int ans = 0;
for (Employee next : cur.nexts) {
ans += process1(next, false);
}
return ans;
} else { // 如果cur的上级不来的话,cur可以选,可以来也可以不来
int p1 = cur.happy;
int p2 = 0;
for (Employee next : cur.nexts) {
p1 += process1(next, true);
p2 += process1(next, false);
}
return Math.max(p1, p2);
}
}
力扣337. 打家劫舍 III
解法:时间复杂度O(n),因为是利用二叉树后序遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
class Info {
int yes;
int no;
public Info(int y, int n) {
yes = y;
no = n;
}
}
public int rob(TreeNode root) {
Info rootInfo = process(root);
return Math.max(rootInfo.yes, rootInfo.no);
}
public Info process(TreeNode root) {
if (root == null) {
return new Info(0, 0);
}
int yes = root.val;
int no = 0;
Info leftInfo = process(root.left);
Info rightInfo = process(root.right);
yes += leftInfo.no;
yes += rightInfo.no;
no += Math.max(leftInfo.yes, leftInfo.no);
no += Math.max(rightInfo.yes, rightInfo.no);
return new Info(yes, no);
}
}