算法

【体系学习008】前缀树与基数排序

Posted by Hilda on September 25, 2025

前缀树、不基于比较的排序、排序稳定性

1.前缀树(trie树)

1.1前缀树概念

1）单个字符串中，字符从前到后的加到一棵多叉树上 2）字符放在路上，节点上有专属的数据项（常见的是pass和end值） 3）所有样本都这样添加，如果没有路就新建，如有路就复用 4）沿途节点的pass值增加1，每个字符串结束时来到的节点end值增加1

可以完成前缀相关的查询

例如一个简单的记录了”abc”、”abd”、”bcf”、”abcd” 这四个字符串的前缀树如下图所示：

image-20250924183149541

注意：在 Java 中，将字符串（或数组）作为键放入 HashMap 的时间复杂度通常不被认为是严格的 O(1)，主要原因在于计算哈希码本身需要时间。原因如下：

HashMap 的核心思想是通过哈希函数将键映射到数组的索引上，从而实现快速存取。理想情况下，哈希码计算和数组访问都是常数时间操作，因此存取操作的时间复杂度是 O(1)。

然而，当键是字符串（或数组）时，情况变得复杂： String 类的 hashCode() 方法的实现会遍历字符串中的每一个字符来计算哈希码。这意味着，如果字符串的长度为 N，计算其哈希码的时间复杂度就是 O(N)。因此，put 或 get 操作中，计算哈希码这一步的时间复杂度取决于键的长度，而不是一个常数。

另外，尽管哈希函数设计得很好，但不同的键仍可能产生相同的哈希码，这被称为哈希冲突。当发生冲突时，HashMap 会在对应索引位置的链表（或红黑树）上进行遍历。在最坏的情况下，所有键都映射到同一个索引，这时查找操作会退化为对链表的遍历，时间复杂度变为 O(N)，其中 N 是键的数量。但是，对于字符串键，哈希冲突的开销通常被摊销，而哈希码计算的开销则是必然存在的。

1.2实现前缀树(代码)

Node包含三个关键部分：pass 字段用于记录有多少个字符串经过此节点，end 字段则记录以该节点为结尾的完整字符串的数量，而 nexts 数组则存储指向其子节点的引用。nexts 数组的大小通常是26，对应英文字母 ‘a’ 到 ‘z’，通过 (char - 'a') 的方式来计算字符对应的索引。

即nexts[i] 的索引 i 对应一个特定的字符，通常通过 (char - 'a') 的方式计算得出。例如，'b' - 'a' 的结果是 1，所以 nexts[1] 代表字符 ‘b’。

  • 如果 nexts[i] == null，说明从当前节点出发，没有通向字符 i 的路径。
  • 如果 nexts[i] != null，说明存在一条路径，nexts[i] 存放着下一个节点的引用。

这样，就可以高效地执行以下操作：

  • 查找：判断一个字符串是否存在。
  • 前缀查询：查询有多少个字符串以某个前缀开头。（pass值）
  • 插入：将新字符串添加到数据结构中。

Node代码实现如下：

1
2
3
4
5
6
7
8
9
10
11

public class Node {
    int pass;
    int end;
    Node[] nexts;

    public Node() {
        pass = 0;
        end = 0;
        nexts = new Node[26];
    }
}

前缀树结构：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81

public class Trie {
    private Node root;

    public Trie() {
        root = new Node();
    }

    public void insert(String word) {
        if (word == null) {
            return;
        }
        char[] str = word.toCharArray();
        Node node = root;
        node.pass++;
        int path = 0;
        for (char c : str) {
            path = c - 'a';
            if (node.nexts[path] == null) {
                node.nexts[path] = new Node();
            }
            node = node.nexts[path];
            node.pass++;
        }
        node.end++;
    }

    // word这个单词之前加入过几次
    public int search(String word) {
        if (word == null) {
            return 0;
        }
        char[] str = word.toCharArray();
        Node node = root;
        int path = 0;
        for (char c : str) {
            path = c - 'a';
            if (node.nexts[path] == null) {
                return 0;
            }
            node = node.nexts[path];
        }
        return node.end;
    }

    // 所有加入的字符串中，有几个是以pre这个字符串作为前缀的
    public int prefixNumber(String pre) {
        if (pre == null) {
            return 0;
        }
        char[] str = pre.toCharArray();
        int index = 0;
        Node node = root;
        for (char c : str) {
            index = c - 'a';
            if (node.nexts[index] == null) {
                return 0;
            }
            node = node.nexts[index];
        }
        return node.pass;
    }

    public void delete(String word) {
        if (search(word) != 0) {
            char[] str = word.toCharArray();
            int path = 0;
            Node node = root;
            node.pass--;
            for (char c : str) {
                path = c - 'a';
                if (--node.nexts[path].pass == 0) {
                    node.nexts[path] = null;
                    return;
                }
                node = node.nexts[path];
            }
            node.end--;
        }
    }
}

1.3力扣208-实现 Trie (前缀树)

208. 实现 Trie (前缀树)

下面的实现其实pass属性是没必要的，而且end可以替换成一个boolean类型的属性，但是为了更好的拓展，此处就这么写了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72

class Trie {
    
    class Node {
        int pass;
        int end;
        Node[] nexts;

        public Node() {
            pass = 0;
            end = 0;
            nexts = new Node[26];// word 和 prefix 仅由小写英文字母组成
        }
    }

    private Node root;

    public Trie() {
        root = new Node();
    }
    
    public void insert(String word) {
        // 1 <= word.length, prefix.length <= 2000
        char[] str = word.toCharArray();
        int index = 0;
        Node node = root;
        for (char c : str) {
            index = c - 'a';
            if (node.nexts[index] == null) {
                node.nexts[index] = new Node();
            }
            node = node.nexts[index];
            node.pass++;
        }
        node.end++;
    }
    
    public boolean search(String word) {
        Node node = root;
        int index = 0;
        char[] str = word.toCharArray();
        for (char c : str) {
            index = c - 'a';
            if (node.nexts[index] == null) {
                return false;
            }
            node = node.nexts[index];
        }
        return node.end != 0;
    }
    
    public boolean startsWith(String prefix) {
        Node node = root;
        int index = 0;
        char[] str = prefix.toCharArray();
        for (char c : str) {
            index = c - 'a';
            if (node.nexts[index] == null) {
                return false;
            }
            node = node.nexts[index];
        }
        return true;
    }
}

/**
 * Your Trie object will be instantiated and called as such:
 * Trie obj = new Trie();
 * obj.insert(word);
 * boolean param_2 = obj.search(word);
 * boolean param_3 = obj.startsWith(prefix);
 */

上面提及的更加简化的解法就是：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

class Trie {

    class Node {
        // end 计数器可以换成一个布尔值，如果只需要判断是否存在
        // 如果需要记录单词出现的次数，则保留int类型
        boolean isEndOfWord;
        Node[] nexts;

        public Node() {
            isEndOfWord = false;
            nexts = new Node[26];
        }
    }

    private Node root;

    public Trie() {
        root = new Node();
    }
    
    public void insert(String word) {
        Node node = root;
        for (char c : word.toCharArray()) {
            int index = c - 'a';
            if (node.nexts[index] == null) {
                node.nexts[index] = new Node();
            }
            node = node.nexts[index];
        }
        node.isEndOfWord = true;
    }
    
    public boolean search(String word) {
        Node node = root;
        for (char c : word.toCharArray()) {
            int index = c - 'a';
            if (node.nexts[index] == null) {
                return false;
            }
            node = node.nexts[index];
        }
        return node.isEndOfWord;
    }
    
    public boolean startsWith(String prefix) {
        Node node = root;
        for (char c : prefix.toCharArray()) {
            int index = c - 'a';
            if (node.nexts[index] == null) {
                return false;
            }
            node = node.nexts[index];
        }
        return true;
    }
}

1.4力扣-1804. 实现 Trie （前缀树） II

1804. 实现 Trie （前缀树） II

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91

class Trie {


    class Node {
        int pass;
        int end;
        Node[] nexts;

        public Node() {
            pass = 0;
            end = 0;
            nexts = new Node[26];// word 和 prefix 只包含小写英文字母。
        }
    }
    private Node root;

    public Trie() {
        root = new Node();
    }
    
    public void insert(String word) {
        // 1 <= word.length, prefix.length <= 2000
        char[] str = word.toCharArray();
        int index = 0;
        Node node = root;
        node.pass++;
        for (char c : str) {
            index = c - 'a';
            if (node.nexts[index] == null) {
                node.nexts[index] = new Node();
            }
            node = node.nexts[index];
            node.pass++;
        }
        node.end++;
    }
    
    public int countWordsEqualTo(String word) {
        char[] str = word.toCharArray();
        int index = 0;
        Node node = root;
        for (char c : str) {
            index = c - 'a';
            if (node.nexts[index]== null) {
                return 0;
            }
            node = node.nexts[index];
        }
        return node.end;
    }
    
    public int countWordsStartingWith(String prefix) {
        char[] str = prefix.toCharArray();
        int index = 0;
        Node node = root;
        for (char c : str) {
            index = c - 'a';
            if (node.nexts[index]== null) {
                return 0;
            }
            node = node.nexts[index];
        }
        return node.pass;
    }
    
    public void erase(String word) {
        // 保证每次调用 erase 时，字符串 word 总是存在于前缀树中。
        char[] str = word.toCharArray();
        int index = 0;
        Node node = root;
        node.pass--;
        for (char c : str) {
            index = c - 'a';
            if (--node.nexts[index].pass == 0) {
                node.nexts[index] = null;
                return;
            }
            node = node.nexts[index];
        }
        node.end--;
    }
}

/**
 * Your Trie object will be instantiated and called as such:
 * Trie obj = new Trie();
 * obj.insert(word);
 * int param_2 = obj.countWordsEqualTo(word);
 * int param_3 = obj.countWordsStartingWith(prefix);
 * obj.erase(word);
 */

2.基数(Radix)排序

2.1前缀分区技巧

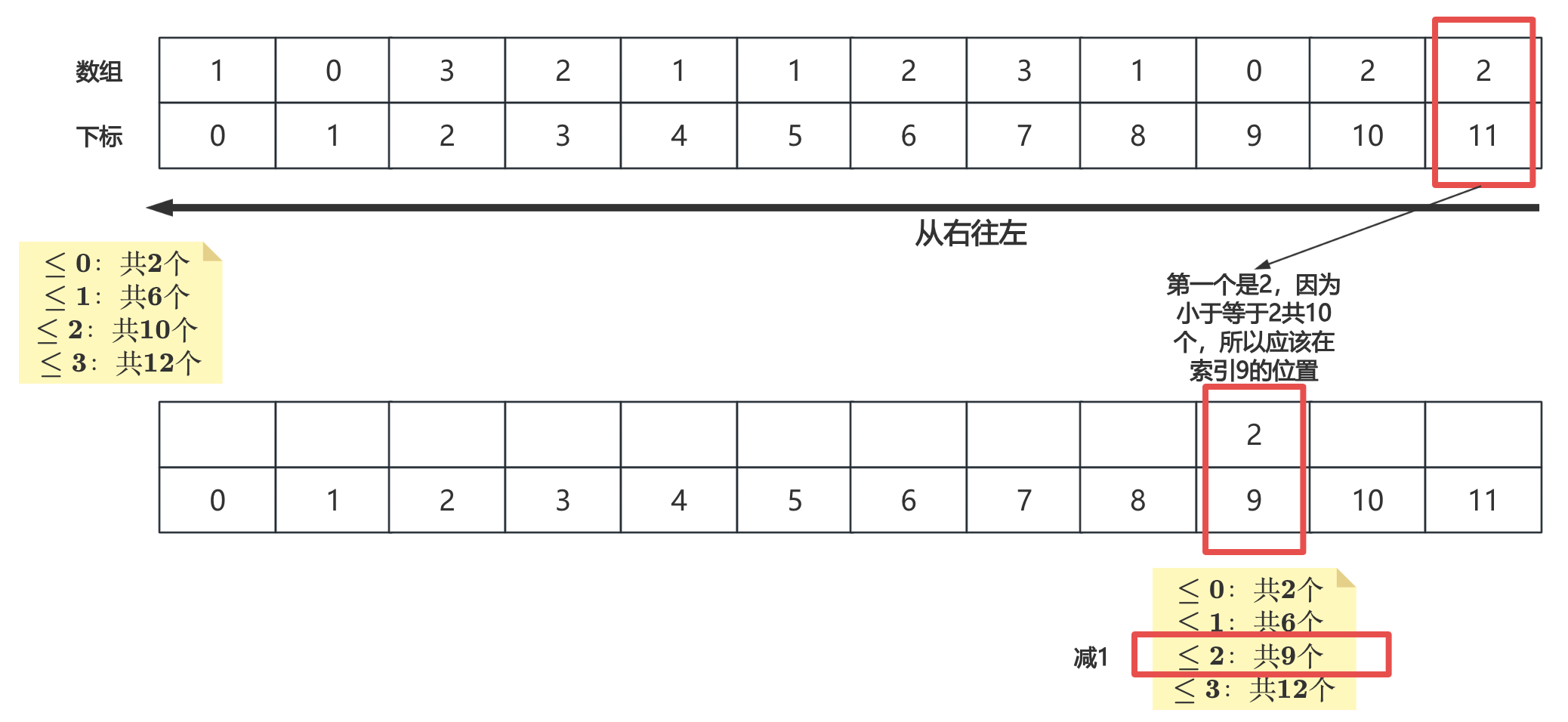
image-20250925152257059

2.2基数排序的原理

基于比较的排序 只需要定义好两个对象之间怎么比较即可，对象的数据特征并不关心，很通用 不基于比较的排序 和比较无关的排序，对于对象的数据特征有要求，并不通用

计数排序，非常简单，但是数值范围比较大了就不行了

基数排序的实现细节，非常优雅的一个实现 关键点：前缀数量分区的技巧、数字提取某一位的技巧 时间复杂度O(n)，额外空间复杂度O(m)，其中m是桶的个数（即几进制），需要辅助空间做类似桶的作用，来不停的装入、弹出数字

一般来讲，计数排序要求，样本是整数，且范围比较窄 一般来讲，基数排序要求，样本是10进制的非负整数 如果不是就需要转化，代码里做了转化，并且代码里可以设置任何进制来进行排序 一旦比较的对象不再是常规数字，那么改写代价的增加是显而易见的，所以不基于比较的排序并不通用

2.3基数排序的代码实现-填函数

测试链接 : https://leetcode.cn/problems/sort-an-array/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73

class Solution {
	// 可以设置进制，不一定10进制，随你设置
	public static int BASE = 10;

	public static int MAXN = 50001;

	public static int[] help = new int[MAXN];

	public static int[] cnts = new int[BASE];

	public static int[] sortArray(int[] arr) {
		if (arr.length > 1) {
			// 如果会溢出，那么要改用long类型数组来排序
			int n = arr.length;
			// 找到数组中的最小值
			int min = arr[0];
			for (int i = 1; i < n; i++) {
				min = Math.min(min, arr[i]);
			}
			int max = 0;
			for (int i = 0; i < n; i++) {
				// 数组中的每个数字，减去数组中的最小值，就把arr转成了非负数组
				arr[i] -= min;
				// 记录数组中的最大值
				max = Math.max(max, arr[i]);
			}
			// 根据最大值在BASE进制下的位数，决定基数排序做多少轮
			radixSort(arr, n, bits(max));
			// 数组中所有数都减去了最小值，所以最后不要忘了还原
			for (int i = 0; i < n; i++) {
				arr[i] += min;
			}
		}
		return arr;
	}

	// 返回number在BASE进制下有几位
	public static int bits(int number) {
		int ans = 0;
		while (number > 0) {
			ans++;
			number /= BASE;
		}
		return ans;
	}

	// 基数排序核心代码
	// arr内要保证没有负数
	// n是arr的长度
	// bits是arr中最大值在BASE进制下有几位
	public static void radixSort(int[] arr, int n, int bits) {
		// 理解的时候可以假设BASE = 10
		for (int offset = 1; bits > 0; offset *= BASE, bits--) {
			Arrays.fill(cnts, 0);
			for (int i = 0; i < n; i++) {
				// 数字提取某一位的技巧
				cnts[(arr[i] / offset) % BASE]++;
			}
			// 处理成前缀次数累加的形式
			for (int i = 1; i < BASE; i++) {
				cnts[i] = cnts[i] + cnts[i - 1];
			}
			for (int i = n - 1; i >= 0; i--) {
				// 前缀数量分区的技巧
				// 数字提取某一位的技巧
				help[--cnts[(arr[i] / offset) % BASE]] = arr[i];
			}
			for (int i = 0; i < n; i++) {
				arr[i] = help[i];
			}
		}
	}
}

2.3基数排序的代码实现- ACM风格

洛谷上有ACM风格题：https://www.luogu.com.cn/problem/P1177

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78

import java.io.*;
import java.util.*;
public class Main{
    public static int MAXN = 100001;
    public static int BASE = 10;
    public static int[] help = new int[MAXN];
    public static int[] cnts = new int[BASE];
    public static void main(String[] args) throws IOException{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StreamTokenizer in = new StreamTokenizer(br);
        PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
        while (in.nextToken() != StreamTokenizer.TT_EOF) {
            int n = (int)in.nval;
            in.nextToken();
            int[] arr = new int[n];
            for (int i = 0;i < n;i++) {
                arr[i] = (int)in.nval;
                in.nextToken();
            }
            int min = arr[0];
            for (int i = 1;i < n;i++) {
                min = Math.min(min, arr[i]);
            }
            int diff = (~min + 1);
            int max = arr[0];
            for (int i = 0;i < n;i++) {
                arr[i] += diff;
                max = Math.max(max, arr[i]);
            }
            int bits = getBits(max);
            radixSort(arr, n, bits);
            // 恢复
            for (int i = 0;i < n;i++) {
                arr[i] -= diff;
            }
            // 输出
            for (int i = 0;i < n;i++) {
                out.print(arr[i] + " ");
            }
        }
        out.flush();
        br.close();
        out.close();
    }

    public static void  radixSort(int[] arr, int n, int bits) {
        
        for (int offset = 1;bits > 0;bits--, offset *= BASE) {
            Arrays.fill(cnts, 0);
            // 填cnts数组
            for (int i = 0;i < n;i++) {
                cnts[arr[i] / offset % BASE]++;
            }

            // 累加cnts
            for (int i = 1;i < BASE;i++) {
                cnts[i] = cnts[i - 1] + cnts[i];
            }
            // 倒桶  反着
            for (int i = n - 1;i >= 0;i--) {
                help[--cnts[arr[i] / offset % BASE]] = arr[i];
            }
            // help
            for (int i = 0;i < n;i++) {
                arr[i] = help[i];
            }
        }
    }

    public static int getBits(int n) {
        int ans = 0;
        while (n != 0) {
            ans++;
            n /= BASE;
        }
        return ans;
    }
}
CATALOG
    FEATURED TAGS
    书籍阅读 算法 人工智能AI基础 python基础 力扣 numpy pandas 机器学习-吴恩达 机器学习算法 matplotlib spring6 算法题库 Java基础 java集合 ollama工具 python爬虫
    FRIENDS