这里的“位图”不是指图像格式，而是数据结构中的位图（Bitmap），以及利用位运算实现加减乘除的算法。这是计算机科学和编程领域中的两个经典且重要的概念。

1.位图的功能

引言：如果想要存储一个数，往往我们会想到java的容器，比如HashSet。HashSet基于哈希表（Hash Table），每个元素（Integer 对象,特别注意java的容器都会自动装箱，不存储基本数据结构int等）通过哈希函数计算出一个哈希值，然后存储在哈希表对应的位置。HashSet<Integer> 存储的是 Integer 类的实例。一个 Integer 对象在 64 位 JVM 中通常占用 16 到 24 字节（取决于JVM实现），再加上哈希表本身的开销（指针、数组等）。所以，每个数字需要4 字节（32 位 int）或更多来存储，再加上对象头、哈希表数组、以及可能存在的链表或红黑树等开销。所以这显然是不小的空间。

但是如果使用位图，考虑一个int类型的变量，比如就是int set = 0，有4B，及32bit，每个比特置1就可以表示0-31这么多情况。显然不需要一个java容器去专门存储了。

但是，一个int只能表示0-31，才32个数，这会不会太少了？如果存储更多的数呢？这时候可以用int[]去存储，比如要表示0-1023，那么需要int[] arr = new int[32]就可以了。

位图的基本思想是，用一个比特位（bit）来代表一个数字是否存在。一个 int 有 32 位，所以能表示 32 个数字的状态。如果我们需要表示超过 32 个数字，就用一个 int 数组，每个 int 元素都代表一个 32 个数字的区间。

要将一个数字 k 存入位图或进行查询，我们需要做两步简单的计算：

确定数组索引（arrIndex）：这个数字属于哪个 int 元素？
- 计算方法：arrIndex = k / 32
确定位索引（bitIndex）：在这个 int 元素里，它是第几位？
- 计算方法：bitIndex = k % 32

通过这种方式，位图可以轻松地扩展到处理海量数据。无论是表示 0 到 1023，还是 0 到 10 亿，你只需要根据数字范围创建相应大小的 int 数组即可。它始终保持每个数字仅占用一个比特位的极致空间效率，以及 O(1) 的超快存取速度。

实现一个位图BitMap会比哈希表省至少32倍。

2.位图的实现

public class BitMap {
    long[] bits;

    public BitMap(int max) {
        // 表示0必须要1个long类型的数，所以要max + 64
        // >>6 就是除以64  因为用的是long类型
        bits = new long[(max + 64) >> 6];
    }

    public void add(int value) {
        bits[value >> 6] |= (1L << (value & 63));
    }
    public void delete(int value) {
        bits[value >> 6] &= ~(1L << (value & 63));
    }
    public boolean contains(int value) {
        return ((bits[value >> 6] ) & (1L << (value & 63))) != 0;
    }
}

和java的HashSet进行测试，对数器如下：

public static void main(String[] args) {
    System.out.println("测试开始");
    int max = 100000;
    BitMap bitMap = new BitMap(max);
    HashSet<Integer> test = new HashSet<>();
    int testTime = 10000000;
    for (int i = 0;i < testTime;i++) {
        int num = (int)(Math.random() * (max));
        double decide = Math.random();
        if (decide < 0.33) {
            // add
            bitMap.add(num);
            test.add(num);
        } else if(decide < 0.66) {
            bitMap.delete(num);
            test.remove(num);
        } else {
            if (bitMap.contains(num) != test.contains(num)) {
                System.out.println("Oops!!!");
                break;
            }
        }
    }
    for (int i = 0;i < max ;i++) {
        if (bitMap.contains(i) != test.contains(i)) {
            System.out.println("Oops!!!");
            break;
        }
    }

    System.out.println("测试成功！！！");
}

3.位运算实现加减乘除

3.1加法

异或就是无进位相加。

与完之后再左移1位就是进位信息。

两个数相加的结果就是两个数异或（无进位信息）后加上与（进位信息）的结果。

一直这么做（得到无进位信息和进位信息），直到进位信息是0，就会得到最终的不进位信息，这个不进位信息就是原来求和的结果。

实现代码：

public int add(int a, int b) {
    int sum = a;
    while (b != 0) {
        sum = a ^ b;
        b = (a & b) << 1;
        a = sum;
    }
    return sum;
}

3.2减法

a-b就是a+(-b)

要得到一个数的相反数，只需要取反加1。但是不能出现加法，所以求a+b就是add(a, add(~b, 1))

代码：

public int minus(int a, int b) {
    return add(a, negNum(b));
}

public int negNum(int n) {
    return add(~n, 1);
}

3.3乘法

二进制的乘法：

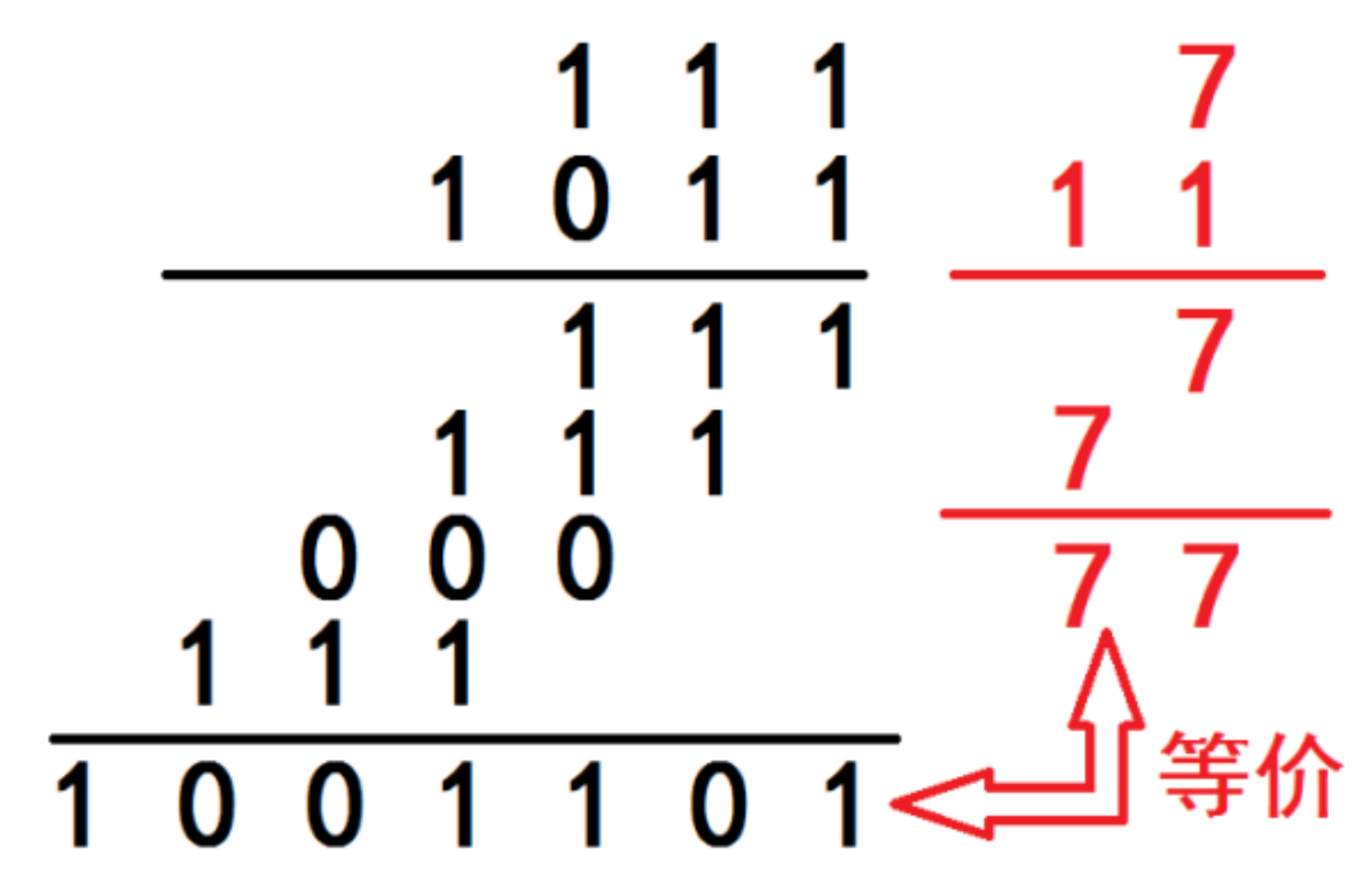
代码：

public int multi(int a, int b) {
    int ans = 0;
    while (b != 0) {
        if ((b & 1) != 0) {
            ans = add(ans, a);
        }
        a <<= 1;
        b >>>= 1;
    }
    return ans;
}

3.4除法

原理看图：

举一个例子

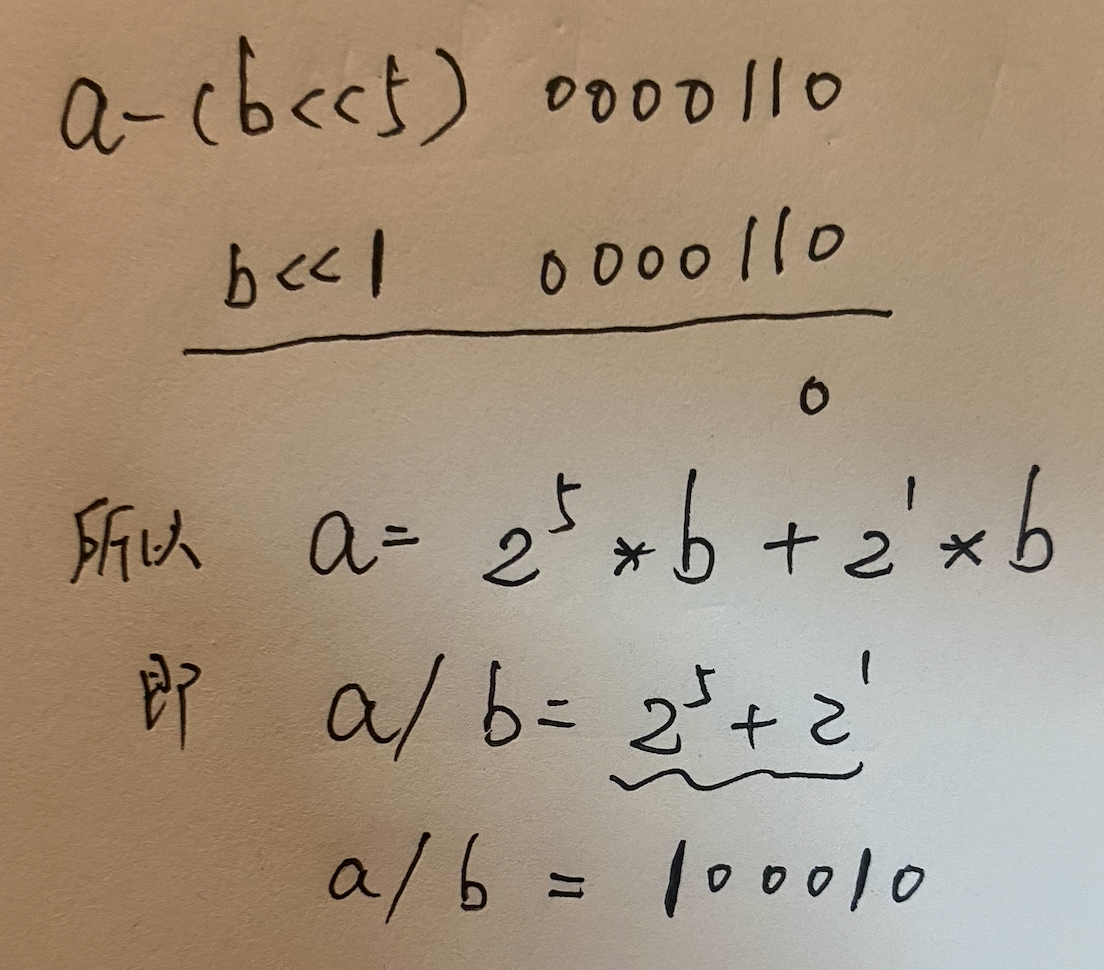
但是，实际写代码时，要注意，b左移和a右移是一回事，但是b左移需要判断有没有移过了（b移超过了才知道需要左移几位），但是a右移不需要移超过，所以写代码考虑a右移而不是b左移。（而且要考虑a如果第一个1在紧挨着符号位0的下一个位置，此时b要左移到符号位才知道移动超了，但是此时b就变成了负数，这显然也不是我们想要的）

代码：

public int div(int a, int b) {
    // 变成绝对值
    int x = isNeg(a) ? negNum(a) : a;
    int y = isNeg(b) ? negNum(b) : b;
    int ans = 0;
    for (int i = 30;i >= 0;i = minus(i, 1)) {
        if ((x >> i) >= y) {
            ans |= (1 << i);
            x = minus(x, (y << i));
        }
    }
    return isNeg(a) ^ isNeg(b) ? negNum(ans) : ans;
}

为什么从30开始尝试？不应该是31吗？

因为已经有了int x = isNeg(a) ? negNum(a) : a;，已经将x调整为非负了，那么x的第一位一定是0（java的int是有符号的表示，第一位如果是非负数就是0，第一位如果是负数就是1，所以现在x必然第一位一定是0），这样x的第一个1一定从第2个位置开始，只需要考虑右移31种情况就可以了，即i=0~31。

上面这个结果是向下取整的结果（比如9/4就是得到2）

但是上面这个方法有个局限：系统最小值，因为它无法转成绝对值。

如何解决系统最小值转绝对值

考虑下面几种情况：

如果a,b都是系统最小值，a/b=1
如果b是系统最小值（此时a不论是什么值，但不是系统最小值），a/b=0
如果a是系统最小值，b不是系统最小值。比如a=-15, b=3，此时系统最小值是-15，系统最大值是14。先求（-15+1）/3=-4，由-4求(-4)*3=-12，-12和-15差(-15-(-12))=-3，而-3/3=-1，最后结果就是(-4+(-1))=-5，绕过了系统最小值问题。即用下面的流程归纳：
- 要计算a/b，流程是(a+1)/b=c，c*b=d，a-d=e，e/b=f，最终结果就是c+f
- 如果a是系统最小值，而b是-1，那么本来这个结果也表示不了，所以力扣上约定，此时返回系统最大值即可。
如果a,b都不是系统最小值，这用上面div的方法就可以了。

代码如下：

public int divide(int a, int b) {
    if (a == Integer.MIN_VALUE && b == Integer.MIN_VALUE) {
        return 1;
    }else if (b == Integer.MIN_VALUE) {
        return 0;
    } else if (a == Integer.MIN_VALUE) {
        if (b == -1) {
            return Integer.MAX_VALUE;
        } else {
            int c = div(add(a, 1), b);
            int d = multi(c, b);
            int e = minus(a, d);
            int f = div(e, b);
            return add(c, f);
        }
    } else {
        return div(a, b);
    }
}

测试链接：https://leetcode.cn/problems/divide-two-integers/description/

https://ac.nowcoder.com/acm/problem/21988 （ACM风格）

如果只用a/b来做（题目没有要求不能）：

如果用位运算实现：

【新手005】位图的实现，用位运算实现加减乘除