1.概率实验：验证 Math.random() 方法生成随机数的均匀性

Math.random() 生成的随机数在 [0.0, 1.0) 区间内均匀分布，下面是一个证明均匀分布的小实验：

public class Test_Random {

    public static void main(String[] args) {
        int N = 100000;
        int count = 0;
        for (int i = 0;i < N;i++) {
            if (Math.random() < 0.3) count++;
        }
        System.out.println((double) count / (double) N);
    }
}

Math.random() 基于 Random 类的线性同余生成器（LCG），通过生成均匀分布的整数并归一化为 [0.0, 1.0) 范围的浮点数，保证了均匀分布。

推广：Math.random() * K应该返回[0, K)，而(int)(Math.random() * K)（等概率）返回[0, K - 1]上的一个整数。

例如：(int)(Math.random() * 10)等概率返回[0, 9]范围上的一个整数。

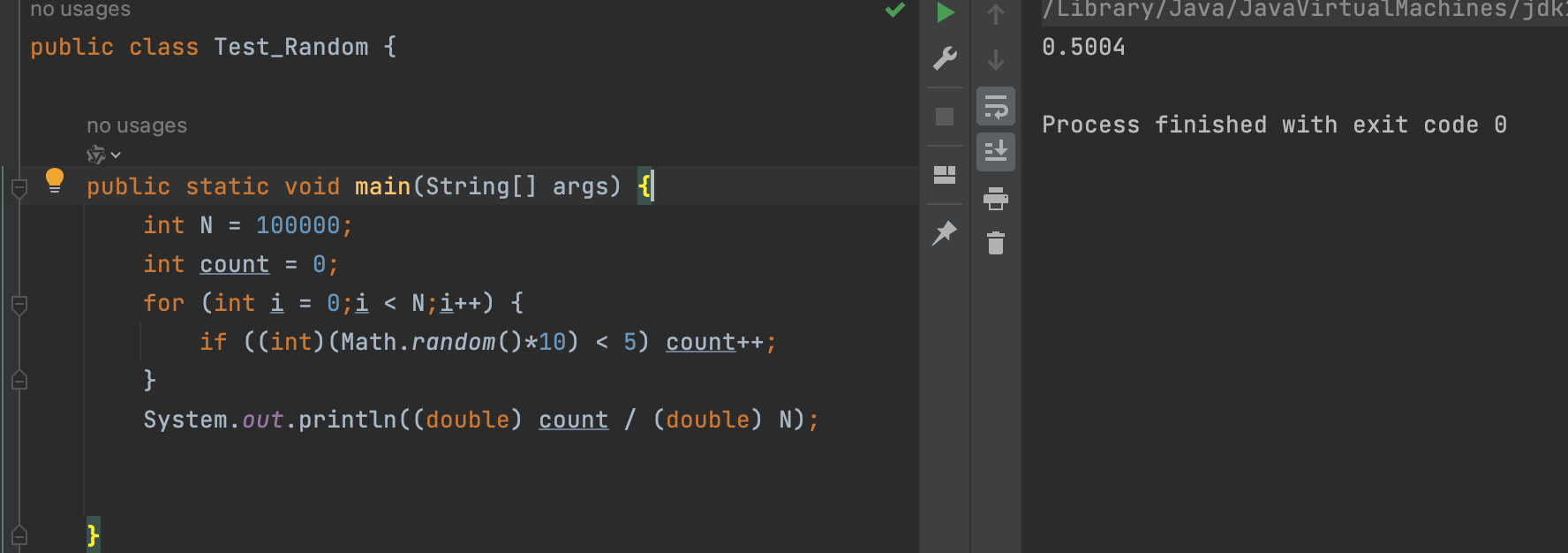
下面代码的输出大约就是0.5

int N = 100000;
int count = 0;
for (int i = 0;i < N;i++) {
    if ((int)(Math.random()*10) < 5) count++;
}
System.out.println((double) count / (double) N);

再例如下面代码：countsArr中每个元素的值大约就是100000/10=10000（countsArr统计每次随机生成的数）

int N = 100000;
int[] countsArr = new int[10];
for (int i = 0;i < N;i++) {
    countsArr[(int)(Math.random() * 10)]++;
}
System.out.println(Arrays.toString(countsArr));

这就是写对数器的基础，想要生成什么样的随机数就生成什么样的随机数。

一个问题，现在出现的某个数概率是线性的。例如，0-1上出现小于0-0.3的概率是30%，出现0-0.8的数的概率是80%。现在想要的效果不是线性的，例如\(x^2\)，比如0-1上出现0-0.3的概率是9%，出现0-0.8的数的概率是64%，该如何实现？

解决方法：

public static void main(String[] args) {
    int N = 100000;
    int count = 0;
    for (int i = 0;i < N;i++) {
        if (xToXPower2() < 0.8) count++;
    }
    System.out.println((double) count / (double) N);
}

public static double xToXPower2() {
    return Math.max(Math.random(), Math.random());
}

上面代码的输出大概是0.64

为什么呢？分析 Math.max(Math.random(), Math.random()) 的累积分布函数。

假设 Y1 和 Y2 是两个独立的随机变量，它们都服从 [0,1) 上的均匀分布。我们定义一个新的随机变量 X=max(Y1,Y2)。现在我们想要求 X 的累积分布函数 \(F_X(x)=P(X<x)\)，也就是 P(max(Y1,Y2)<x)。

根据概率论的知识： P(max(Y1,Y2)<x) 的意思是，max(Y1,Y2) 的值小于 x。这等价于 Y1 和 Y2 的值都小于 x。

所以： P(max(Y1,Y2)<x)=P(Y1<x 和 Y2<x)

因为 Y1 和 Y2 是独立的，所以我们可以将它们的概率相乘： P(Y1<x 和 Y2<x)=P(Y1<x)∗P(Y2<x)

因为 Y1 和 Y2 都服从 [0,1) 上的均匀分布，所以它们各自的累积分布函数是\(F_Y(x)=x\)。也就是说： P(Y1<x)=x ，P(Y2<x)=x

把这两个结果代入上面的等式： P(max(Y1,Y2)<x)=x∗x=x2

因此，Math.max(Math.random(), Math.random()) 生成的随机数，其累积分布函数正是 \(F_X(x)=x^2\)。

同理，也可以使得达到\(x^3\)的效果，比如0-1上出现0-0.3的概率是2.7%，如下：

public static void main(String[] args) {
    int N = 100000;
    int count = 0;
    for (int i = 0;i < N;i++) {
        if (xToXPower3() < 0.3) count++;
    }
    System.out.println((double) count / (double) N);
}

public static double xToXPower3() {
    return Math.max(Math.random(),Math.max(Math.random(), Math.random()));
}

再考虑一点，把xToXPower2中的max改成min，那么最终的概率是多少？

应该是\(1-(1-x)^2\)，不信可以通过代码验证。

解释：同样来分析它的累积分布函数 \(F_X(x)=P(X≤x)\)。这里 \(X=min(Y1,Y2)\)，其中 Y1 和 Y2 都是均匀分布在 [0,1) 的随机变量。

\(P(X≤x)\) 意味着 \(min(Y1,Y2)\) 的值小于或等于 x。这发生的情况是：Y1 小于等于 x，或者 Y2 小于等于 x（或两者都小于等于 x）。直接计算这个概率有点复杂，但我们可以利用 逆向思维。

\[P(X≤x)=1−P(X>x)\]

而 \(P(X>x)\) 的意思是 \(min(Y1,Y2)\) 的值大于 x。这只有在Y1 和 Y2 的值都大于 x 的情况下才会发生。

所以：\(P(X>x)=P(Y1>x and Y2>x)\)

因为 Y1 和 Y2 是独立的，所以我们可以将概率相乘：

\[P(Y1>x and Y2>x)=P(Y1>x)×P(Y2>x)\]

因为 Y1 和 Y2 是均匀分布在 [0,1) 区间，所以： \(P(Y1>x)=1−P(Y1≤x)=1−x P(Y2>x)=1−P(Y2≤x)=1−x\)

将这两个结果代入：

P(X>x)=(1−x)×(1−x)=(1−x)2

最后，我们回到最初的等式：

\[P(X≤x)=1−P(X>x)=1−(1−x)^2\]

所以，Math.min(Math.random(), Math.random()) 生成的随机数，其累积分布函数是 \(F_X(x)=1−(1−x)^2\)。

2.从1-5随机到1-7随机

有一个函数\(f\)，可以等概率返回1-5（即等概率返回1，2，3，4，5），在不调用其余随机机制的情况下（例如不再调用Math.random()，只有\(f\)是可以唯一借助的随机机制），如何利用\(f\)等概率返回1-7（即等概率返回1，2，3，4，5，6，7）？

解法思路：如何从\(f\)到\(g\)？（\(f\)是条件函数，等概率返回1-5，\(g\)是目标函数，等概率返回1-7）

首先将\(f\)改造为0-1发生器：如果\(f\)返回1或者2，则最终为0；如果\(f\)返回4或者5，则最终为1；如果\(f\)是3，则反复调用\(f\)，直到\(f\)返回不是3。（1-5的概率都是20%，但是得到3的概率会均摊到1，2，4，5上，所以得到的0-1发生器结果均匀分布）

public class Random1To7From1To5 {
    public static void main(String[] args) {
        // 验证0-1发生器
        int N = 1000000;
        int count = 0;
        for (int i = 0;i < N;i++) {
            if (condition()==1) {
                count++;
            }
        }
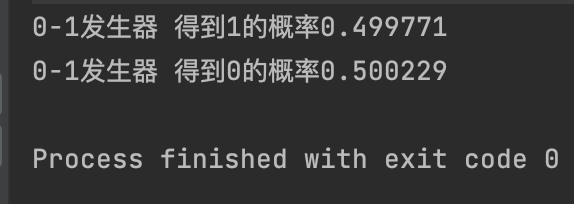
        System.out.println("0-1发生器 得到1的概率"+(double) count / (double) N);
        System.out.println("0-1发生器 得到0的概率"+(double) (N - count) / (double) N);
    }

    // 等概率返回1-5
    public static int f() {
        return (int)(Math.random()*5) + 1;
    }
    // 0-1发生器
    public static int condition() {
        int ans = 0;
        do{
            ans = f();
        }while(ans==3);
        return ans < 3 ? 0 : 1;
    }
}

上面代码的2个输出都大约是0.5：

然后思路是：得到1-7的等概率，即得到0-6的等概率。0-6需要3bit的二进制。每个bit调用上面的condition得到。所以得到000-111的概率都是相等的(即等概率返回0-7上的整数)。但是要求是1-7等概率返回，所以和condition思路类似，得到0就不断调用，直到结果不为0，将得到0的概率均摊到1-7上。以上就是利用一个能等概率返回1到5的随机函数，来生成一个能等概率返回1到7的随机数。代码完整如下：

public class Random1To7From1To5 {
    public static void main(String[] args) {
        // 验证0-1发生器
        int N = 1000000;
        int count[] = new int[8];
        for (int i = 0;i < N;i++) {
            count[g()]++;
        }
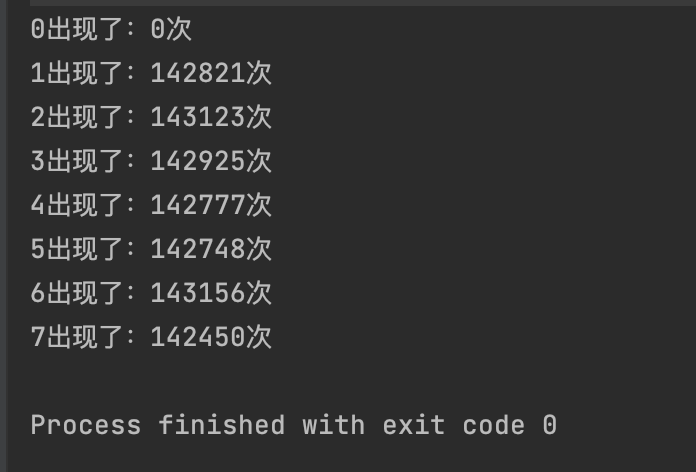
        for (int i = 0;i < 8;i++) {
            System.out.println(i + "出现了：" + count[i] + "次");
        }

    }

    // 等概率返回1-5
    public static int f() {
        return (int)(Math.random()*5) + 1;
    }
    // 0-1发生器
    public static int condition() {
        int ans = 0;
        do{
            ans = f();
        }while(ans==3);
        return ans < 3 ? 0 : 1;
    }

    // 000-111  等概率返回
    public static int target() {
        return condition() + (condition() << 1) + (condition() << 2);
    }

    // 最终的g函数
    public static int g() {
        int ans = 0;
        do{
            ans = target();
        }while (ans == 0);
        return ans;
    }
}

执行结果是：

现在可以将上述代码进行扩展了，使得其更佳通用一些。

任意给出start1,end1,start2,end2，如何实现？

例如，如何从\(f(3,19)\)转化成\(g(17,56)\)？

首先3-19有19-3+1=17个数，一半就是8个数，所以3-10上就返回0，12-19上就返回1，11就重做。—-》等概率得到了0-1发生器

（如果是偶数个数，则不需要重做）

\(g(17, 56)\)可以转换成\(g(0,39)\)，需要k个二进制位（如果是0-39，则需要\(log_240\)向上取整就是6位，k=6），则调用k次发生器。而如果得到的数是40-63则一直重做，概率又被均摊了。搞定！

所以我写了一个版本的代码，实现上面由\(f(a,b)\)到\(g(c,d)\)的功能。

public class RandomCToDFromAToB {

    public static void main(String[] args) {
        // f(a,b)--->g(c,d)
        int A = 3, B = 19, C = 17, D = 56;
        int N = 1000000;
        int[] count = new int[D - C + 1];
//        int count = 0;
        for (int i = 0;i < N;i++) {
            count[g(A, B, C, D) - C]++;
        }
        for (int i = 0;i < (D - C + 1);i++) {
            System.out.println((i+C) + "出现了:"+count[i]+ "次");
        }

    }

    public static int f(int a, int b) {
        // 3-19   0-16
        return (int)(Math.random() * (b - a + 1)) + a;
    }

    // 0-1发生器
    public static int condition(int A, int B) {
        int ans;
        int sum = B - A + 1; // 随机范围的长度

        // 如果范围长度是奇数，通过循环排除中间值
        if (sum % 2 != 0) {
            int middle = A + sum / 2;
            do {
                ans = f(A, B);
            } while (ans == middle);
        } else {
            // 如果范围长度是偶数，则直接调用即可
            ans = f(A, B);
        }

        // 无论奇偶，剩下的数字都被分成两个大小相等的集合
        int half = sum / 2;
        int middleVal = A + half;

        return ans < middleVal ? 0 : 1;
    }

    public static int target(int A, int B, int C, int D) {
        // 17-56   0-39   6bit二进制   2^6=64    2^5 = 32
        // 56-17 + 1 = 40
        int k = (int)(Math.ceil(Math.log(D - C + 1) / Math.log(2)));
        int ans = 0;
        // 需要不断做的段是40-63  sum = 40
        int sum = D - C + 1;
        do{
            // 调用k次发生器
            ans = 0;
            for (int i = 0;i < k;i++) {
                ans += (condition(A, B) << i);
            }
        }while(ans >= sum && ans <= Math.pow(2, k) - 1);
        return ans;
    }

    public static int g(int A, int B, int C, int D) {
        return target(A, B, C, D) + C;

    }
}

然后我用gemini优化了一个更好的版本：

public class OptimizedRandomCToDFromAToB {

    public static void main(String[] args) {
        // f(a,b)--->g(c,d)
        int A = 3, B = 19, C = 17, D = 56;
        int N = 1000000;
        int[] count = new int[D - C + 1];

        for (int i = 0; i < N; i++) {
            count[g(A, B, C, D) - C]++;
        }
        for (int i = 0; i < (D - C + 1); i++) {
            System.out.println((i + C) + "出现了:" + count[i] + "次");
        }
    }

    public static int f(int a, int b) {
        return (int) (Math.random() * (b - a + 1)) + a;
    }

    public static int condition(int A, int B) {
        int ans;
        int sum = B - A + 1;
        int middleVal;

        if (sum % 2 != 0) {
            middleVal = A + sum / 2;
            do {
                ans = f(A, B);
            } while (ans == middleVal);
        } else {
            ans = f(A, B);
            middleVal = A + sum / 2;
        }
        return ans < middleVal ? 0 : 1;
    }

    // 优化后的 target 函数
    public static int target(int A, int B, int C, int D) {
        int range = D - C; // 目标范围的长度（从0开始）
        int k = 0; // 需要的二进制位数
        while ((1 << k) <= range) {
            k++;
        }

        int ans;
        do {
            ans = 0;
            for (int i = 0; i < k; i++) {
                ans |= (condition(A, B) << i);
            }
        } while (ans > range); // 循环条件更简洁

        return ans;
    }

    public static int g(int A, int B, int C, int D) {
        return target(A, B, C, D) + C;
    }
}

3.01不等概率随机到01等概率随机

有函数\(f\)以\(p\)概率返回0，以\(1-p\)概率返回1，\(p\)始终不等于0.5（且p是固定的），即函数\(f\)以不等的概率返回0和1。如何利用函数\(f\)得到函数\(g\)，使得\(g\)等概率返回0和1？

思路：两次调用函数\(f\)，返回的只可能是00，11，01，10，而返回00或者11都重做；返回01则最终返回0，返回10则最终返回1。因为返回01和10的概率都是\(p(1-p)\)。

public class FromNonEqualToEqual {

    public static void main(String[] args) {
        int N = 1000000;
        int count = 0;
        for(int i = 0;i < N;i++) {
            if(g()==1) count++;
        }
        System.out.println("出现1的次数:"+count);
        System.out.println("出现0的次数:"+(N - count));
    }

    public static int f() {
        return Math.random() < 0.65 ? 0 : 1;
    }

    public static int g() {
        int ans = 0;
        do{
            ans = f();
        }while (ans == f());// 第一次如果和第二次相等，即00或者11
        return ans;
    }
}

【新手002】Math.random()随机函数

1.概率实验：验证 Math.random() 方法生成随机数的均匀性

2.从1-5随机到1-7随机

3.01不等概率随机到01等概率随机

CATALOG

FEATURED TAGS

FRIENDS