1.折线图 (Line Plot)
折线图是显示数据随时间或有序类别变化的趋势的常用图表。它通过连接一系列数据点来展示数值型变量的连续变化。
主要函数是 plt.plot(*args, scalex=True, scaley=True, data=None, **kwargs) 或 ax.plot(*args, **kwargs)。
*args: 可以接受多种形式的输入,最常见的是(x, y)坐标对。plot(y): 如果只提供一个序列y,它会被绘制为 Y 轴值,而 X 轴值将自动生成为0, 1, ..., len(y)-1。plot(x, y): 绘制y相对于x的折线。plot(x, y, fmt, ...):fmt是一个格式字符串,用于快速指定线条颜色、标记和线条样式,例如'r--o'表示红色虚线带圆圈标记。
scalex,scaley: 布尔值,如果为True(默认),则自动缩放 X/Y 轴以适应数据。data: 可以是一个字典或 Pandas DataFrame,允许通过字符串名称引用列。**kwargs: 其他可选参数,用于精细控制线条的样式:color/c: 线条颜色 (例如'red','#FF0000',(1, 0, 0))。linestyle/ls: 线条样式 (例如'-','--','-.',':','None')。linewidth/lw: 线条宽度 (浮点数)。marker: 数据点标记样式 (例如'o','*','.','+','x','s'(正方形),'D'(菱形))。markersize/ms: 标记大小。markerfacecolor/mfc: 标记填充颜色。markeredgecolor/mec: 标记边缘颜色。markeredgewidth/mew: 标记边缘宽度。label: 用于图例的标签字符串。
一图多线: 在同一个 Axes 对象上多次调用 plot() 函数,可以在同一张图上绘制多条折线,它们会共享相同的坐标轴。
多图布局: 通过 plt.subplots() 或 plt.subplot() 可以创建多个子图,在不同的子图上绘制不同的折线图,用于对比或展示不同维度的数据。
选择题
-
在
plt.plot(y)中,如果只提供一个序列y,X 轴的默认值是什么?A. 0 到
len(y)B. 1 到len(y)C. 0 到len(y)-1D. 1 到len(y)-1答案:C
-
以下哪个参数用于在折线图上指定数据点的标记样式? A.
linestyleB.linewidthC.markerD.color答案:C,
marker用于设置数据点的形状,linestyle设置线条的连接方式,linewidth设置线条粗细,color设置线条颜色。
编程题
- 创建一个折线图,绘制函数\(y=e^{−0.5x}sin(2x)\) 在 \(x \in[0,10]\) 范围内的曲线。
- 曲线颜色为橙色,线条样式为点划线 (
-.),线条宽度为 2。 - 每隔 5 个数据点添加一个菱形 (
'D') 标记,标记大小为 8,标记边缘颜色为黑色,填充颜色为黄色。 - 添加标题 “Damped Sine Wave”。
- 添加 X 轴标签 “Time (s)” 和 Y 轴标签 “Amplitude”。
- 显示图例和网格。
- 曲线颜色为橙色,线条样式为点划线 (
1
2
3
4
5
6
7
8
9
10
x = np.linspace(0, 10+0.0001, 100)
y = np.exp(-x/2) * np.sin(2*x)
plt.figure(figsize=(10, 8))
plt.plot(x, y, color="orange", ls="-.", lw=2, marker="D", markevery=5, markersize=5, markeredgecolor="k", markerfacecolor="yellow", label=r"$e^{-x/2}*sin(2x)$")
plt.title("Damped Sine Wave")
plt.xlabel("Time(s)")
plt.ylabel("Amplitude")
plt.legend()
plt.grid()
plt.show()

2.柱状图 (Bar Chart)
柱状图用于比较不同类别之间的数据大小,或者显示单个类别中不同子类别的数据分布。
主要函数是 plt.bar(x, height, width=0.8, bottom=None, *, align='center', data=None, **kwargs) 或 ax.bar(...)。
x: X 轴上的类别位置。通常是整数序列或类别名称。height: 每个柱子的高度(Y 轴值)。width: 柱子的宽度(默认为 0.8)。bottom: 每个柱子的基线 Y 坐标。这对于创建堆叠柱状图非常重要。align: 柱子与 X 轴刻度标签的对齐方式 ('center'(默认) 或'edge')。**kwargs: 其他可选参数,如color,edgecolor,linewidth,label,yerr(Y 轴误差条) 等。
堆叠柱状图 (Stacked Bar Chart): 通过多次调用 plt.bar(),并利用 bottom 参数,可以将不同类别的数据堆叠在同一个 X 轴位置上。每次调用时,bottom 参数设置为前一个柱子的高度之和。
分组带标签柱状图 (Grouped Bar Chart with Labels): 为了在同一 X 轴位置上并排显示多个柱子(代表不同的组),需要手动调整每个柱子的 X 坐标。通常会使用 np.arange(len(labels)) 作为基础 X 坐标,然后通过加减 width/2 等方式来偏移柱子的位置。
添加标签/注释: matplotlib.patches.Rectangle 对象代表了每个柱子。可以通过 bar() 函数的返回值来获取这些 Rectangle 对象,然后使用 rect.get_height() 获取柱子高度,rect.get_x() 和 rect.get_width() 获取柱子的位置和宽度,进而使用 plt.text() 在柱子上方添加数值标签。
柱状图的核心是
matplotlib.patches.Rectangle对象。每次调用plt.bar(),Matplotlib 都会为每个数据点创建一个Rectangle对象,并将其添加到Axes中。
- 堆叠原理: 当绘制堆叠柱状图时,
bottom参数告诉 Matplotlib 从哪个 Y 坐标开始绘制当前的Rectangle。这样,后续的柱子就会在前一个柱子的顶部开始绘制,从而形成堆叠效果。- 分组原理: 分组柱状图通过调整每个柱子的 X 坐标来实现。例如,对于两个组,第一个组的柱子可以绘制在
x - width/2,第二个组的柱子绘制在x + width/2,这样它们就会以x为中心并排显示。- 文本注释:
plt.text()函数用于在图表的数据坐标系中添加文本。通过获取柱子的几何属性(如rect.get_x(),rect.get_width(),rect.get_height()),可以精确计算文本的放置位置,使其位于柱子的上方并居中。
水平柱状图 (plt.barh()): 与 plt.bar() 类似,但用于绘制水平柱状图,X 轴表示值,Y 轴表示类别。
误差条(误差棒): 可以使用 yerr 或 xerr 参数为柱子添加误差条,表示数据的变异性。
如果误差棒明显过长,甚至超过柱状图的长度,那么这个实验数据就存在明显的变异性,可重复性较差;反之,误差棒长短都比较均一,则误差较小,实验数据较为稳定,离散性小,可信度高。
颜色映射: 对于数值型数据,可以使用颜色映射 (Colormap) 来为柱子着色,以表示第三个维度的数据。
自定义柱子样式: 可以通过 edgecolor, linewidth, hatch (填充图案) 等参数来进一步自定义柱子的外观。
应用场景:
- 类别数据比较: 比较不同产品销量、不同地区人口、不同班级成绩等。
- 调查问卷结果: 展示不同选项的投票比例。
- 资源分配: 显示不同项目或部门的资源消耗。
- 机器学习模型评估:
- 分类报告: 绘制每个类别的精确率、召回率、F1 分数柱状图。
- 特征重要性: 绘制特征重要性得分的柱状图,直观展示哪些特征对模型贡献最大。
- 模型性能对比: 比较不同模型在同一指标上的表现(例如,不同算法的准确率)。
- 文本分类词频: 统计不同类别文本中关键词的词频,并用柱状图展示。
2.1 堆叠柱状图
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
labels = ["Group A", "Group B", "Group C", "Group D", "Group E"]
man_scores = np.random.randint(50, 80, size=len(labels))
woman_scores = np.random.randint(60, 90, size=len(labels))
men_std = np.random.randint(2, 8, size=len(labels))
women_std = np.random.randint(2, 8, size=len(labels))
plt.figure(figsize=(10, 6))
width=0.5 # 柱子的宽度
# 使用 `yerr` 或 `xerr` 参数为柱子添加误差条
plt.bar(labels, man_scores, width, yerr=man_std, label="Men", color="skyblue", edgecolor="blue", lw=1)
# 如果是堆叠柱状图:bottom=man_scores
plt.bar(labels, woman_scores, width, yerr=women_std, label="Women", bottom=man_scores, color="lightcoral", edgecolor="red", lw=1)
plt.ylabel("分数")
plt.title("分数(男生/女生)")
plt.legend()
plt.grid(True, ls=":", alpha=0.7)
plt.show()

2.2 分组带标签柱状图
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
plt.figure(figsize=(12, 7))
x_pos = np.arange(len(labels))
width = 0.35
rects1 = plt.bar(x_pos - width / 2, man_scores, width, label="Men", color="lightgreen", edgecolor="green", lw=1)
rects2 = plt.bar(x_pos + width / 2, woman_scores, width, label="Women", color="lightsalmon", edgecolor="brown", lw=1)
plt.ylabel("分数")
plt.title("分组带标签柱状图")
plt.xticks(x_pos, labels, rotation=45, ha="right")
plt.legend()
plt.grid(axis="y", ls=":", alpha=0.7)
# 添加数值标签的辅助函数
def autolabel(rects):
for rect in rects:
height = rect.get_height()
plt.text(rect.get_x() + rect.get_width()/2, height + 1, f"{height}", ha="center", va="bottom", fontsize=10, color="gray")
autolabel(rects1)
autolabel(rects2)
plt.tight_layout()
plt.show()

选择题
-
在
plt.bar()函数中,哪个参数用于创建堆叠柱状图? A.widthB.alignC.bottomD.yerr答案:C,
bottom参数指定了柱子的起始 Y 坐标,通过累加前一个柱子的高度可以实现堆叠。 -
要获取
plt.bar()绘制的单个柱子的高度,可以使用其返回的Rectangle对象上的哪个方法?A.
get_x()B.get_width()C.get_height()D.get_label()答案:C,
get_height()返回柱子的垂直高度。get_x()返回柱子的左边缘 X 坐标,get_width()返回柱子的宽度。
编程题
- 创建一个分组柱状图,比较两家公司(”Company A”, “Company B”)在三个季度(”Q1”, “Q2”, “Q3”)的销售额。
- Company A 的销售额:Q1=120, Q2=150, Q3=130
- Company B 的销售额:Q1=100, Q2=180, Q3=110
- 使用不同的颜色表示两家公司。
- 为每个柱子添加销售额数值标签。
- 添加标题 “Quarterly Sales Comparison”。
- 添加 X 轴标签 “Quarter” 和 Y 轴标签 “Sales (Millions)”。
- 添加图例。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
labels = ["Q1", "Q2", "Q3"]
dataA = [120, 150, 130]
dataB = [100, 180, 110]
plt.figure(figsize=(12, 7))
x_pos = np.arange(len(labels))
width = 0.35
rects1 = plt.bar(x_pos - width / 2, dataA, width, label="companyA", color="lightgreen", edgecolor="green", lw=1)
rects2 = plt.bar(x_pos + width / 2, dataB, width, label="companyB", color="lightsalmon", edgecolor="brown", lw=1)
plt.ylabel("Sales (Millions)")
plt.xlabel("Quarter")
plt.title("Quarterly Sales Comparison")
plt.xticks(x_pos, labels, rotation=45, ha="right")
plt.legend()
plt.grid(axis="y", ls=":", alpha=0.7)
# 添加数值标签的辅助函数
def autolabel(rects):
for rect in rects:
height = rect.get_height()
plt.text(rect.get_x() + rect.get_width()/2, height + 1, f"{height}", ha="center", va="bottom", fontsize=10, color="gray")
autolabel(rects1)
autolabel(rects2)
plt.tight_layout()
plt.show()

3.极坐标图 (Polar Plot)
极坐标图用于显示数据在圆形坐标系中的分布,通常用于表示周期性数据或方向性数据。
创建极坐标图的关键在于在创建 Axes 对象时指定 projection='polar'。
主要函数是 plt.subplot(..., projection='polar', **kwargs) 或 fig.add_subplot(..., projection='polar', **kwargs)。
projection='polar': 这是将Axes转换为极坐标系的关键参数。
1
2
3
4
5
6
7
8
# 准备数据
r_line = np.arange(0, 2* np.pi + 0.00001, 0.01) # 角度
y_line = r_line # 半径随角度线性增长,形成螺旋线
fig = plt.figure(figsize=(10, 8))
# 定义极坐标系axes
ax_polor_line = plt.subplot(111, projection="polar", facecolor="lightyellow")

在极坐标系中,数据点由半径 r 和角度 theta 定义:
r: 距离圆心的距离(相当于笛卡尔坐标系的 Y 轴)。theta: 角度(相当于笛卡尔坐标系的 X 轴),通常以弧度表示。
极坐标线形图 (Polar Line Plot): 使用 ax.plot(theta, r, **kwargs) 在极坐标系中绘制折线图。
ax.set_rmax(value): 设置半径轴的最大值。ax.set_rticks(ticks): 设置半径轴的刻度位置。ax.set_rlabel_position(angle): 设置半径刻度标签相对于径向网格线的角度位置。ax.grid(True): 显示极坐标网格线。ax.set_thetagrids(angles, labels): 设置角度网格线和标签。
极坐标柱状图 (Polar Bar Chart): 使用 ax.bar(theta, r, width=..., bottom=0.0, **kwargs) 在极坐标系中绘制柱状图。
theta: 每个柱子的起始角度。r: 每个柱子的半径(高度)。width: 每个柱子在角度方向上的宽度(弧度)。bottom: 柱子的起始半径(默认为 0.0,即从圆心开始)。
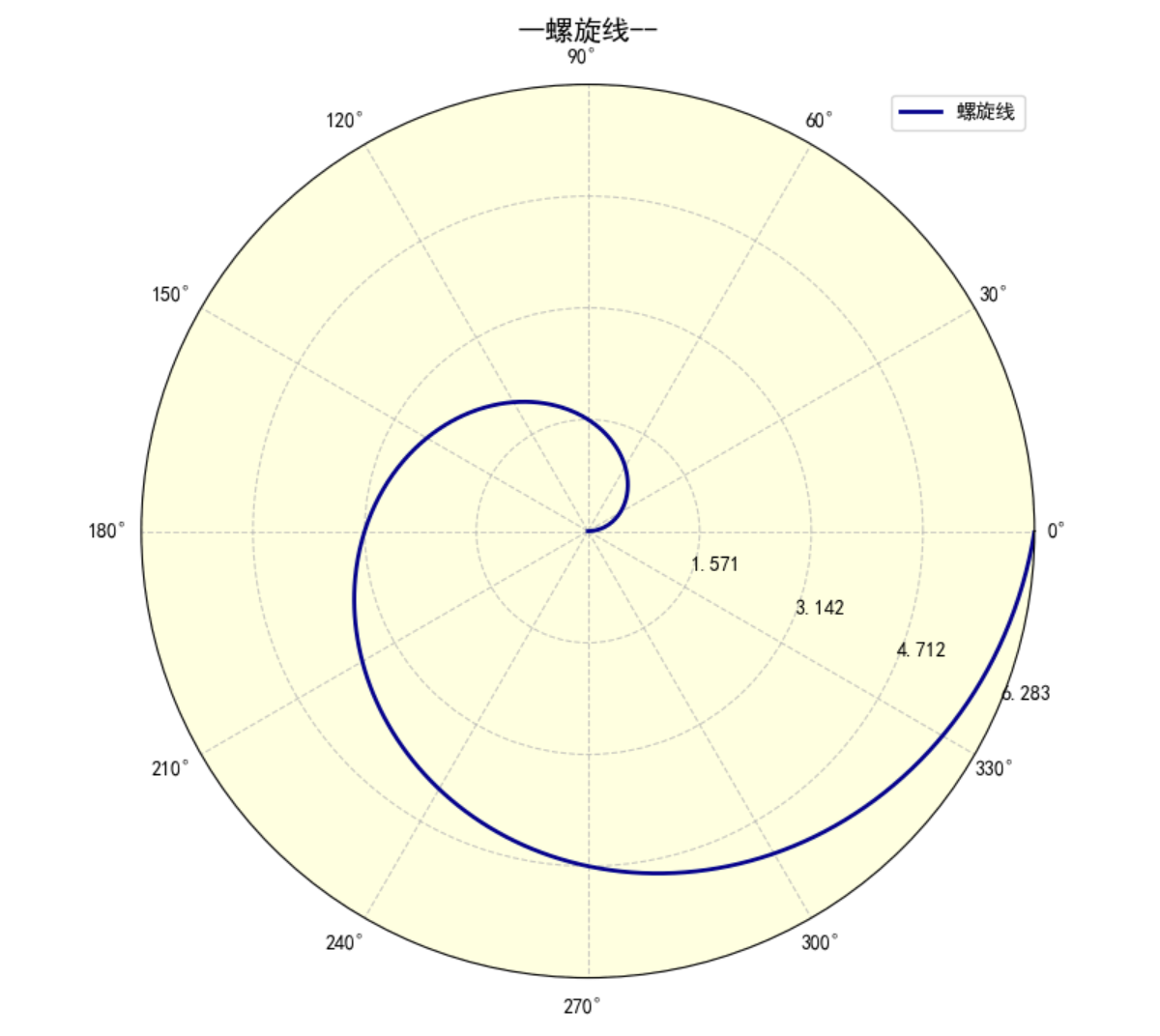
3.1 极坐标线性图
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# 准备数据
r_line = np.arange(0, 2* np.pi + 0.00001, 0.01) # 角度
y_line = r_line # 半径随角度线性增长,形成螺旋线
fig = plt.figure(figsize=(10, 8))
# 定义极坐标系axes
ax_polor_line = plt.subplot(111, projection="polar", facecolor="lightyellow")
# 绘制极坐标系线性图
ax_polor_line.plot(r_line, y_line, color="darkblue", lw=2, label="螺旋线")
# 设置半径轴属性
ax_polor_line.set_rmax(2*np.pi + 0.00001)
ax_polor_line.set_rticks([np.pi / 2, np.pi, 3 * np.pi / 2, 2 * np.pi])
ax_polor_line.set_rlabel_position(-22.5) # 设置半径刻度标签的位置
# 设置角度轴属性
ax_polor_line.set_thetagrids(np.arange(0, 360, 30)) # 角度网格线,每30度一个
ax_polor_line.grid(True, ls="--", alpha=0.7)
ax_polor_line.set_title("--螺旋线--", va = "bottom", pad = 20, fontsize=14)
ax_polor_line.legend(loc="upper right")
plt.show()
3.2 极坐标柱状图
例子:风向频率
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
# 准备数据
N = 12 # 12个方向
theta_bar = np.linspace(0.0, 2 * np.pi, N, endpoint=False) # 角度
radii_bar = 10 + np.random.rand(N) * 5 # 随机半径
width_bar = (2 * np.pi) / N * 0.9 # 每个柱子的角度宽度,留出一点间隙
# 随机生成的颜色
# Colormap将数据集中每个点的数值映射为颜色,从而用颜色来直观地展示数据分布和变化
colors=plt.cm.viridis(radii_bar / radii_bar.max()) # 使用Colormap生成颜色
fig = plt.figure(figsize=(8, 8))
# 定义极坐标
ax_polor_bar = plt.subplot(111, projection="polar")
# 极坐标柱状图绘制
ax_polor_bar.bar(theta_bar, radii_bar, width=width_bar, bottom=0.0, color=colors, edgecolor="k", lw=0.5)
# 设置标题和半径轴
ax_polor_bar.set_title("风向频率图(极坐标系柱状图)", va="bottom", pad=20, fontsize=14)
ax_polor_bar.set_rmax(16) # 最大半径
ax_polor_bar.set_rticks([5, 10, 15]) # 半径的刻度
ax_polor_bar.set_rlabel_position(90)
# 设置角度轴标签
direction_labels = ["N", "NNE", "NE", "ENE", "E", "ESE",
"SE", "SSE", "S", "SSW", "SW", "WSW"]
ax_polor_bar.set_xticks(theta_bar)
ax_polor_bar.set_xticklabels(direction_labels)
ax_polor_bar.tick_params(axis="x", labelsize=10) # 角度标签字体大小
# 网格
ax_polor_bar.grid(True, ls="--", alpha=0.7)
plt.show()

选择题
-
要在 Matplotlib 中创建极坐标图,在创建
Axes对象时必须设置哪个参数?A.
polar=TrueB.projection='polar'C.coords='polar'D.type='polar'答案:B
-
在极坐标柱状图中,
width参数控制的是什么?A. 柱子的半径。 B. 柱子的高度。 C. 柱子在角度方向上的宽度。 D. 柱子在径向方向上的宽度。
答案:C,在极坐标柱状图中,
width定义了每个柱子在角度维度上占据的弧度大小。
编程题
- 创建一个极坐标线形图,绘制一个心形线 (Cardioid)。
- 心形线的参数方程通常为 r=a(1+cos(theta))。
- 设置 a=1,theta 从 0 到 2pi。
- 曲线颜色为红色,线条宽度为 2。
- 设置半径轴的最大值为 2。
- 添加标题 “Cardioid on Polar Axis”。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# 准备数据
a = 1
theta = np.arange(0, 2* np.pi + 0.00001, 0.01) # 角度
y_line = a * (1 + np.cos(theta)) # 半径随角度线性增长,形成螺旋线
fig = plt.figure(figsize=(10, 8))
# 定义极坐标系axes
ax_polor_line = plt.subplot(111, projection="polar", facecolor="lightyellow")
# 绘制极坐标系线性图
ax_polor_line.plot(r_line, y_line, color="red", lw=2, label="螺旋线")
# 设置半径轴属性
ax_polor_line.set_rmax(2)
ax_polor_line.set_rticks([np.pi / 2, np.pi, 3 * np.pi / 2, 2 * np.pi])
ax_polor_line.set_rlabel_position(-22.5) # 设置半径刻度标签的位置
# 设置角度轴属性
ax_polor_line.set_thetagrids(np.arange(0, 360, 30)) # 角度网格线,每30度一个
ax_polor_line.grid(True, ls="--", alpha=0.7)
ax_polor_line.set_title("Cardioid on Polar Axis", va = "bottom", pad = 20, fontsize=14)
ax_polor_line.legend(loc="upper right")
plt.show()

4.直方图 (Histogram)
直方图用于显示数值型数据的分布情况,它将数据范围划分为一系列区间(bin),然后统计每个区间内数据点的数量或频率。
主要函数是 plt.hist(x, bins=10, range=None, density=False, weights=None, cumulative=False, histtype='bar', align='mid', orientation='vertical', rwidth=None, log=False, color=None, label=None, stacked=False, **kwargs) 或 ax.hist(...)。
x: 要绘制直方图的数值型数据(一维数组或序列)。bins: 区间的数量或定义区间边界的序列。- 整数: 定义等宽区间的数量。
- 序列: 定义每个区间的边界,例如
[0, 10, 20, 30]。
range: 区间的上下限(min, max)。如果未指定,则从数据的最小值到最大值。density: 布尔值,如果为True,则直方图的高度表示概率密度,使得所有柱子的面积之和为 1。如果为False(默认),则高度表示频数(计数)。weights: 与x长度相同的数组,为x中的每个数据点指定权重。cumulative: 布尔值,如果为True,则绘制累积直方图。histtype: 直方图的类型 ('bar'(默认),'barstacked','step','stepfilled')。align: 柱子与 bin 边界的对齐方式 ('left','mid'(默认),'right')。color: 柱子的颜色。label: 用于图例的标签。stacked: 布尔值,如果为True且x是多维数组,则绘制堆叠直方图。
plt.hist() 函数会返回三个值:
n: 每个 bin 中的计数或密度值。bins: bin 的边界数组。patches: 绘制的Rectangle对象列表(每个柱子)。
这些返回值对于后续处理(例如绘制概率密度函数)非常有用。
直方图的绘制涉及以下步骤:
- 分箱 (Binning): 将连续的数值数据划分为离散的区间(bins)。这些区间可以是等宽的,也可以是自定义的。
- 计数: 统计每个区间内数据点的数量。
- 绘制: 将每个区间的计数(或频率/密度)表示为柱子的高度,并在 X 轴上显示区间。
plt.hist()在内部执行这些操作。当density=True时,它会将每个 bin 的计数除以总数据点数和 bin 的宽度,从而将直方图归一化为概率密度函数的形式,使得总面积为 1。这使得直方图可以与理论概率密度函数进行比较。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# 绘制正态分布的概率密度函数
from scipy.stats import norm
# 准备数据
mu = 100 # 均值
sigma = 15 # 标准差
x_data = np.random.normal(loc=mu, scale = sigma, size=10000) # 生成正态分布
fig, ax = plt.subplots(figsize=(10, 6))
# 绘制直方图
# density=True 归一化为概率密度
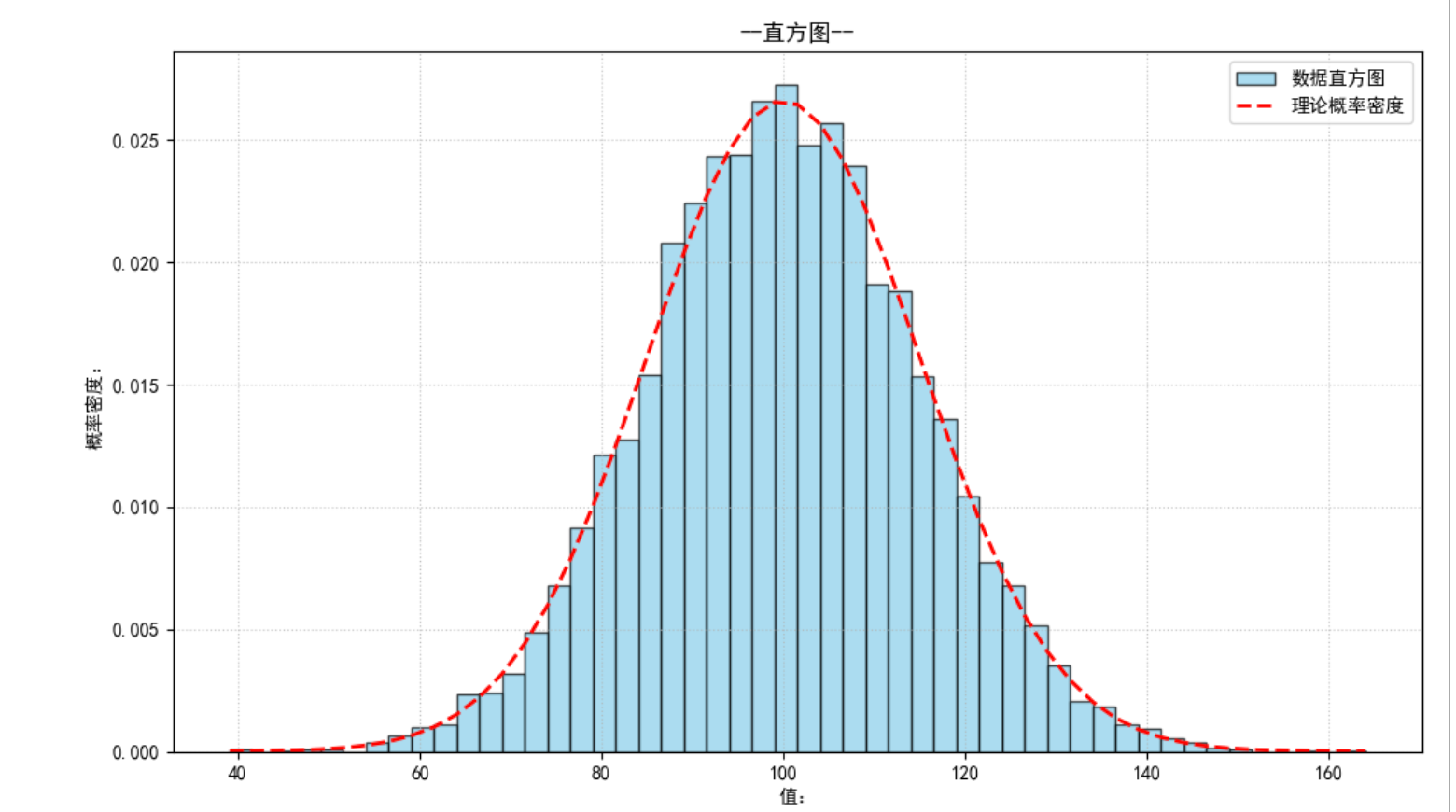
n, bins, patches = ax.hist(x_data, bins = 50, density=True, alpha=0.7, color="skyblue", edgecolor="k", label="数据直方图")
# 绘制理论的概率密度函数(PDF)
y_pdf = norm.pdf(bins, loc=mu, scale=sigma)
ax.plot(bins, y_pdf, "--", color="red", lw=2, label="理论概率密度")
# 添加标题和标签
ax.set_xlabel("值:")
ax.set_ylabel("概率密度:")
ax.set_title("--直方图--")
ax.legend(loc="upper right")
ax.grid(True, ls=":", alpha=0.7)
fig.tight_layout()
plt.show()
拓展:多数据集直方图
非堆叠直方图:
1
2
3
4
5
6
7
8
9
10
11
12
data_group1 = np.random.normal(loc=90, scale=10, size=5000)
data_group2 = np.random.normal(loc=110, scale=12, size=5000)
plt.figure(figsize=(10, 6))
# 非堆叠直方图(默认)
plt.hist([data_group1, data_group2], bins=30, density=True, alpha=0.6, color=["blue", "green"], label=["组1", "组2"])
plt.title("非堆叠直方图")
plt.xlabel("取值")
plt.ylabel("概率密度")
plt.legend()
plt.grid(True, ls=":", alpha=0.7)
plt.show()

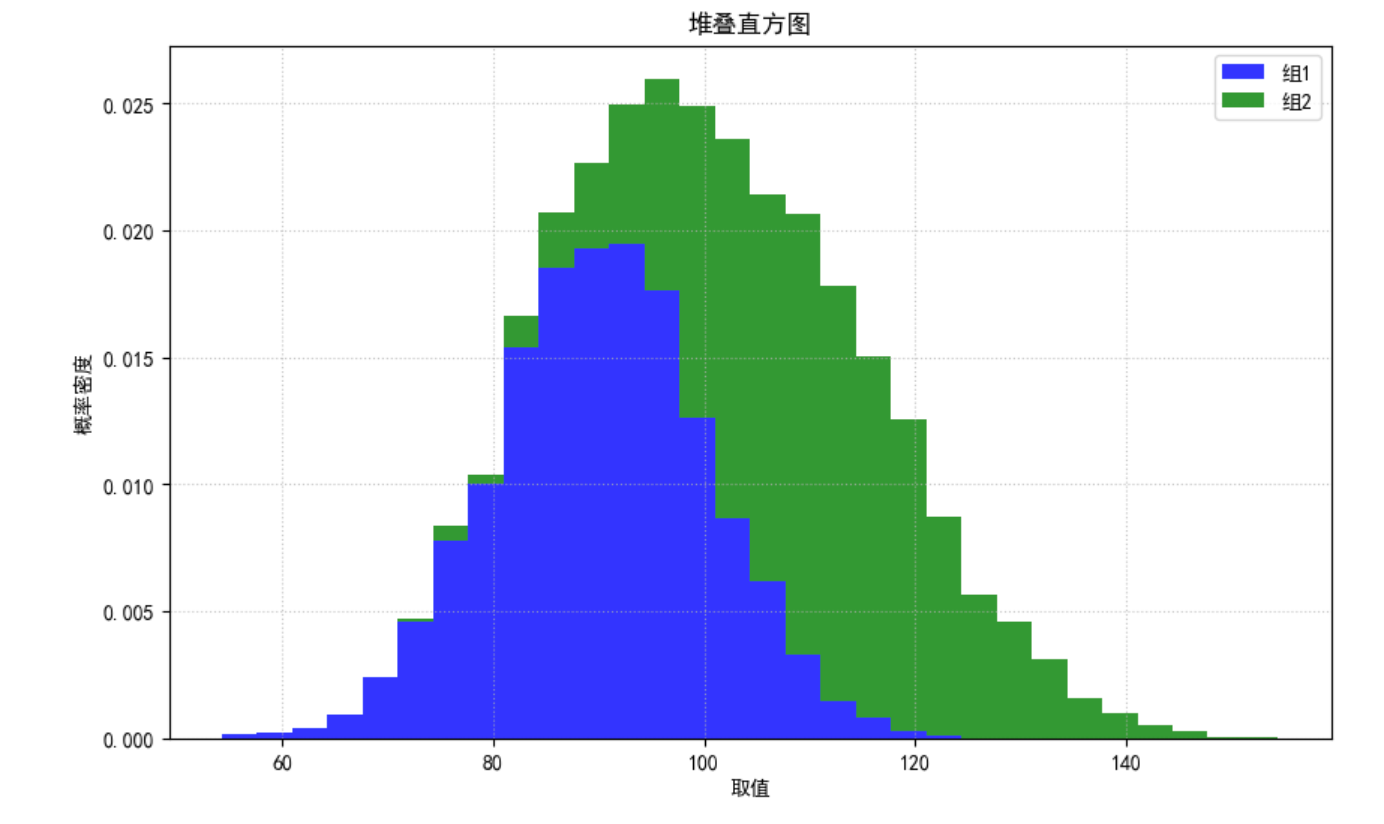
堆叠直方图:
1
2
3
4
5
6
7
8
9
10
11
12
data_group1 = np.random.normal(loc=90, scale=10, size=5000)
data_group2 = np.random.normal(loc=110, scale=12, size=5000)
plt.figure(figsize=(10, 6))
# 堆叠直方图
plt.hist([data_group1, data_group2], bins=30, density=True, alpha=0.8, color=["blue", "green"], label=["组1", "组2"], stacked=True)
plt.title("堆叠直方图")
plt.xlabel("取值")
plt.ylabel("概率密度")
plt.legend()
plt.grid(True, ls=":", alpha=0.7)
plt.show()
选择题
-
在
plt.hist()函数中,如果density参数设置为True,直方图的 Y 轴表示什么?A. 频数(计数) B. 频率 C. 概率密度 D. 累积频率
答案:C, 当
density=True时,直方图被归一化,使得所有柱子的面积之和为 1,Y 轴表示概率密度。 -
plt.hist()函数的bins参数可以接受什么类型的值?A. 整数,表示区间的数量。 B. 序列,表示区间边界。 C. 字符串,表示预设的区间类型。 D. A 和 B 都正确。
答案:D,
bins可以是整数(指定区间数量)或序列(指定区间边界)
编程题
- 生成 10000 个服从标准正态分布(均值 0,标准差 1)的随机数。
- 绘制这些数据的直方图,设置 50 个区间,并将其归一化为概率密度。
- 在同一个图上,叠加绘制标准正态分布的理论概率密度函数曲线。
- 直方图柱子颜色为浅蓝色,边缘为深蓝色。
- 理论曲线颜色为红色,线条样式为虚线。
- 添加标题 “Standard Normal Distribution Histogram and PDF”。
- 添加 X 轴标签 “Value” 和 Y 轴标签 “Probability Density”。
- 显示图例和网格。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# 绘制正态分布的概率密度函数
from scipy.stats import norm
# 准备数据
mu = 0 # 均值
sigma = 1 # 标准差
x_data = np.random.normal(loc=mu, scale = sigma, size=10000) # 生成正态分布
fig, ax = plt.subplots(figsize=(10, 6))
# 绘制直方图
# density=True 归一化为概率密度
n, bins, patches = ax.hist(x_data, bins = 50, density=True, alpha=0.7, color="skyblue", edgecolor="darkblue", label="数据直方图")
# 绘制理论的概率密度函数(PDF)
y_pdf = norm.pdf(bins, loc=mu, scale=sigma)
ax.plot(bins, y_pdf, "--", color="red", lw=2, label="理论概率密度")
# 添加标题和标签
ax.set_xlabel("Value")
ax.set_ylabel("Probability Density")
ax.set_title("tandard Normal Distribution Histogram and PDF")
ax.legend(loc="upper right")
ax.grid(True, ls=":", alpha=0.7)
fig.tight_layout()
plt.show()

5.箱形图 (Box Plot)
箱形图(又称盒须图)是一种用于显示数值数据分布的标准化方法,它能直观地展示数据的中位数、四分位数、离群点等信息。
主要函数是 plt.boxplot(x, notch=False, sym='o', vert=True, whis=1.5, positions=None, widths=None, patch_artist=False, meanline=False, showmeans=False, showcaps=True, showbox=True, showfliers=True, boxprops=None, flierprops=None, medianprops=None, meanprops=None, capprops=None, whiskerprops=None, **kwargs) 或 ax.boxplot(...)。
x: 要绘制箱形图的数据。可以是一个一维数组(绘制一个箱形图),也可以是多个数组的序列(绘制多个箱形图)。notch: 布尔值,如果为True,则箱体中间会有一个凹口,用于表示中位数的置信区间。sym: 离群点的标记样式(默认为'o')。如果设置为'',则不显示离群点。vert: 布尔值,如果为True(默认),则绘制垂直箱形图;如果为False,则绘制水平箱形图。whis: 须的长度。通常是 IQR (四分位距) 的倍数。默认1.5意味着须延伸到Q1 - 1.5 * IQR和Q3 + 1.5 * IQR范围内的最远数据点。超出此范围的点被认为是离群点。labels: 每个箱形图的标签列表。注意这个参数现在已经变成了tick_labels!!!patch_artist: 布尔值,如果为True,则箱体将是Patch对象,可以设置填充颜色等。否则,箱体是Line2D对象。showmeans: 布尔值,如果为True,则显示均值。meanline: 布尔值,如果为True,则均值显示为一条线。flierprops: 离群点属性的字典。boxprops: 箱体属性的字典。medianprops: 中位数线属性的字典。meanprops: 均值标记属性的字典。capprops: 须帽(箱须末端横线)属性的字典。whiskerprops: 须线属性的字典。
箱形图的组成部分:
- 箱体 (Box): 包含数据的 IQR (Interquartile Range),即从第一四分位数 (Q1) 到第三四分位数 (Q3) 的范围。箱体的长度表示数据的集中程度。
- 中位数 (Median): 箱体内的横线,表示数据的中位数 (Q2)。
- 须 (Whiskers): 从箱体延伸出的线,通常延伸到
Q1 - 1.5 * IQR和Q3 + 1.5 * IQR范围内的最远数据点。 - 离群点 (Outliers/Fliers): 超出须范围的数据点,通常用点表示。
小提琴图 (seaborn.violinplot()): 小提琴图是箱形图的增强版,它在箱形图的基础上叠加了核密度估计,可以更详细地展示数据的分布形状。
缺口箱形图 (notch=True): 凹口箱形图的凹口表示中位数的 95% 置信区间。如果两个箱形图的凹口不重叠,则它们的中位数可能存在显著差异。
自定义样式: 通过 boxprops, flierprops 等参数字典,可以高度自定义箱体、离群点、中位数线等各个部分的颜色、线条样式等。
应用场景:
- 比较多组数据的分布: 在不同组别(如不同实验组、不同产品类别)之间比较数据的中心趋势、离散程度和偏态。
- 异常值分析: 快速识别数据集中的离群点。
- A/B 测试结果分析: 比较 A/B 测试中不同变体对某个指标(如转化率、停留时间)的影响分布。
- 模型性能指标分布: 对于交叉验证结果,可以绘制不同折叠(folds)上模型性能指标(如准确率、F1 分数)的箱形图,以评估模型的稳定性。
- 特征工程: 检查不同特征的分布,特别是当特征值范围差异很大时,箱形图可以帮助理解其尺度和异常值。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
# 准备数据,4组不同分布的数据
data1 = np.random.normal(loc=0, scale=1, size=200) # 标准正态
data2 = np.random.normal(loc=2, scale=0.5, size=200) # 均值偏移,方差减小
data3 = np.random.normal(loc=-1, scale=2, size=200) # 均值偏移,方差变大
data4 = np.concatenate((np.random.normal(loc=5, scale=1, size=100), np.random.normal(loc=10, scale=0.5, size=50), np.random.normal(loc=-2, scale=0.8, size=50)))
all_data = [data1, data2, data3, data4]
labels = ["Group_A", "Group_B", "Group_C", "Group_D"]
plt.figure(figsize=(10, 7))
# 绘制箱线图
bplot = plt.boxplot(
all_data,
notch=True,# 箱体中间会有一个凹口,用于表示中位数的置信区间
vert=True, #绘制垂直箱形图
patch_artist=True, # 箱体将是 `Patch` 对象,可以设置填充颜色等
tick_labels=labels,
showmeans=True, # 展示均值
flierprops=dict(marker="o", markerfacecolor="red", markersize=8, alpha=0.6), # 离群点的样式
medianprops=dict(color="blue", lw=2), # 中位数线样式
boxprops=dict(edgecolor="k", lw=1.5), # 箱体边缘样式
whiskerprops=dict(color="gray", ls="--", lw=1), # 须线样式
capprops=dict(color="gray", lw=1.5) # 须帽样式
)
# 为每个箱体设置不同的颜色
colors=["lightblue", "lightgreen", "lightcoral", "lightgoldenrodyellow"]
for patch, color in zip(bplot["boxes"], colors):
patch.set_facecolor(color)
plt.title("数据分布的箱线图", fontsize=16)
plt.xlabel("数据组")
plt.ylabel("值")
plt.grid(axis="y", ls=":", alpha=0.7)
plt.show()
选择题
-
箱形图的箱体部分表示数据分布的哪个范围?
A. 最小值到最大值。 B. 均值加减标准差。 C. 第一四分位数 (Q1) 到第三四分位数 (Q3)。 D. 中位数到最大值。
答案:C,箱体代表数据的 IQR,即中间 50% 的数据。
-
在
plt.boxplot()中,哪个参数用于控制须的长度? A.symB.vertC.whisD.notch答案:C,
whis参数控制须的长度,通常是 IQR 的倍数。
编程题
- 生成三组数据,模拟三个不同班级学生的考试分数:
- 班级 A: 均值 75,标准差 8,200 个学生。
- 班级 B: 均值 80,标准差 5,200 个学生。
- 班级 C: 均值 70,标准差 10,200 个学生。
- 绘制这三组分数的箱形图。
- 箱体颜色分别为蓝色、绿色、红色。
- 显示均值,并用星号 (
'*') 标记。 - 显示离群点,并用绿色菱形 (
'D') 标记。 - 添加标题 “Class Exam Scores Distribution”。
- 添加 X 轴标签 “Class” 和 Y 轴标签 “Score”。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
# 准备数据,4组不同分布的数据
data1 = np.random.normal(loc=75, scale=8, size=200) # 标准正态
data2 = np.random.normal(loc=80, scale=5, size=200) # 均值偏移,方差减小
data3 = np.random.normal(loc=70, scale=10, size=200) # 均值偏移,方差变大
all_data = [data1, data2, data3]
labels = ["班级A", "班级B", "班级C"]
plt.figure(figsize=(10, 7))
# 绘制箱线图
bplot = plt.boxplot(
all_data,
notch=True,# 箱体中间会有一个凹口,用于表示中位数的置信区间
vert=True, #绘制垂直箱形图
patch_artist=True, # 箱体将是 `Patch` 对象,可以设置填充颜色等
tick_labels=labels,
showmeans=True, # 展示均值
flierprops=dict(marker="D", markerfacecolor="green", markersize=8, alpha=0.6), # 离群点的样式
meanprops=dict(marker="*", markerfacecolor="purple", markersize=12, markeredgecolor="yellow"),
medianprops=dict(color="blue", lw=2), # 中位数线样式
boxprops=dict(edgecolor="k", lw=1.5), # 箱体边缘样式
whiskerprops=dict(color="gray", ls="--", lw=1), # 须线样式
capprops=dict(color="gray", lw=1.5) # 须帽样式
)
# 为每个箱体设置不同的颜色
colors=["lightblue", "lightgreen", "red"]
for patch, color in zip(bplot["boxes"], colors):
patch.set_facecolor(color)
plt.title("Class Exam Scores Distribution", fontsize=16)
plt.xlabel("Class")
plt.ylabel("Score")
plt.grid(axis="y", ls=":", alpha=0.7)
plt.show()

6.散点图 (Scatter Plot)
散点图用于显示两个数值变量之间的关系。每个数据点在二维坐标系中由一个点表示。
主要函数是 plt.scatter(x, y, s=None, c=None, marker=None, cmap=None, norm=None, vmin=None, vmax=None, alpha=None, linewidths=None, edgecolors=None, plotnonfinite=False, data=None, **kwargs) 或 ax.scatter(...)。
x,y: 数据点的 X 和 Y 坐标。s: 标记的大小。可以是一个标量(所有点大小相同)或与x,y长度相同的数组(每个点大小不同)。c: 标记的颜色。可以是一个颜色字符串、RGB 元组、颜色名称列表,或者与x,y长度相同的数值数组。如果是数值数组,则颜色会根据颜色映射 (Colormap) 进行映射。marker: 标记样式 (例如'o','s','^','+')。cmap: 颜色映射 (Colormap) 对象或名称(当c是数值数组时)。alpha: 标记的透明度(0到1之间)。linewidths: 标记边缘的线宽。edgecolors: 标记边缘的颜色。label: 用于图例的标签。
散点图非常适合揭示变量之间的相关性、聚类模式或异常值。
气泡图 (Bubble Chart): 当 s 参数被用来表示第三个数值维度时,散点图就变成了气泡图。
颜色条 (Colorbar): 当使用 c 参数进行颜色映射时,通常需要添加一个颜色条 (plt.colorbar()) 来解释颜色与数值的对应关系。
高密度散点图: 对于包含大量数据点的散点图,简单的点可能会重叠严重。可以考虑使用 hexbin() (六边形分箱图) 或 hist2d() (二维直方图) 来显示密度,或者使用 alpha 参数调整透明度。
交互式散点图: 结合 mpl_toolkits.mplot3d 可以绘制三维散点图,结合 plotly 或 bokeh 可以创建交互式散点图。
关于聚类算法的例子:
首先安装库:
1
!pip install scikit-learn
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
import numpy as np
# 生成模拟聚类数据
X, y_true = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=0)
# 运行 KMeans 聚类
kmeans = KMeans(n_clusters=4, random_state=0, n_init=10)
kmeans.fit(X)
y_kmeans = kmeans.predict(X)
plt.figure(figsize=(8, 6))
plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=50, cmap='viridis', alpha=0.8)
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1],
s=200, marker='X', c='red', edgecolor='black', label='Cluster Centers')
plt.title('K-Means Clustering Results', fontsize=16)
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend()
plt.grid(True, linestyle=':', alpha=0.7)
plt.show()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
# 数据准备
np.random.seed(42) # 为了结果可以复现
num_points = 50
data_x = np.random.randn(num_points)
data_y = data_x * 0.8 + np.random.randn(num_points) * 2 # 带了一些噪声
sizes = np.random.randint(50, 500, size=num_points)
colors = np.random.randn(num_points)
plt.figure(figsize=(10, 7))
# 绘制散点图
scatter_plot = plt.scatter(
data_x,
data_y,
s = sizes, # 尺寸(气泡大小)
c = colors,
cmap="viridis", # 颜色映射
alpha=0.6,
marker="o",
edgecolor="k",
lw=0.5
)
# 添加标题和标签
plt.title("散点图绘制", fontsize=16)
plt.xlabel("X 轴值")
plt.ylabel("Y 轴值")
# 添加颜色条(当使用c参数进行颜色映射时非常重要)
cbar = plt.colorbar(scatter_plot)
cbar.set_label("颜色值")
plt.grid(True, ls=":", alpha=0.7)
plt.show()

拓展:不同标记和边缘颜色的散点图
1
2
3
4
5
6
7
8
9
10
11
12
13
14
np.random.seed(42) # 为了结果可以复现
num_points = 150
data_x = np.random.randn(num_points)
data_y = data_x * 0.8 + np.random.randn(num_points) * 2 # 带了一些噪声
plt.figure(figsize=(8, 6))
plt.scatter(data_x[:50], data_y[:50], s=100, c='red', marker='o', edgecolors='blue', linewidths=1.5, label='Group 1')
plt.scatter(data_x[50:100], data_y[50:100], s=150, c='green', marker='s', edgecolors='purple', linewidths=1.5, label='Group 2')
plt.scatter(data_x[100:], data_y[100:], s=200, c='blue', marker='^', edgecolors='orange', linewidths=1.5, label='Group 3')
plt.title('Scatter Plot with Different Markers and Edge Colors')
plt.xlabel('X-axis')
plt.ylabel('Y-axis')
plt.legend()
plt.grid(True, linestyle=':', alpha=0.7)
plt.show()

选择题
-
在
plt.scatter()函数中,哪个参数可以用来根据数据点的第三个数值维度来改变其大小? A.cB.sC.markerD.alpha答案:B,
s: 标记的大小。可以是一个标量(所有点大小相同)或与x,y长度相同的数组(每个点大小不同)。c: 标记的颜色。可以是一个颜色字符串、RGB 元组、颜色名称列表,或者与x,y长度相同的数值数组。如果是数值数组,则颜色会根据颜色映射 (Colormap) 进行映射。
-
如果
plt.scatter()的c参数是一个数值数组,并且你希望颜色能够反映这些数值的大小,你还需要结合使用哪个参数?A.
markerB.alphaC.cmapD.edgecolors答案:C,
cmap: 颜色映射 (Colormap) 对象或名称(当c是数值数组时)。
编程题
- 生成 100 个随机数据点,X 坐标在 [0, 10] 之间,Y 坐标在 [0, 10] 之间。
- 为每个点生成一个随机的大小(在 50 到 500 之间)和一个随机的颜色值(在 0 到 1 之间)。
- 绘制这些点的散点图。
- 使用
viridis颜色映射。 - 点的透明度为 0.7。
- 点的边缘颜色为黑色,线宽为 1。
- 添加标题 “Random Scatter Plot with Size and Color Variation”。
- 添加 X 轴标签 “X-coordinate” 和 Y 轴标签 “Y-coordinate”。
- 添加一个颜色条,标签为 “Random Color Value”。
- 使用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
np.random.seed(42)
num_points = 100
x = np.random.rand(num_points) * 10
y = np.random.rand(num_points) * 10
points_size = np.random.randint(50, 500, size=num_points)
color_values = np.random.rand(num_points)
plt.figure(figsize=(9, 7))
# 绘制散点图
scatter_plot = plt.scatter(x, y, s=points_size, c=color_values, cmap="viridis",
edgecolor="k", lw=1)
plt.title("Random Scatter Plot with Size and Color Variation")
plt.xlabel("X-coordinate")
plt.ylabel("Y-coordinate")
# 添加颜色条(当使用c参数进行颜色映射时非常重要)
cbar = plt.colorbar(scatter_plot)
cbar.set_label("Random Color Value")
plt.grid(True, ls=":", alpha=0.7)
plt.show()

7.饼图 (Pie Chart)
饼图用于显示各部分在整体中所占的比例。它将一个圆形分成若干个扇形,每个扇形的大小与它所代表的数据的比例成正比。
主要函数是 plt.pie(x, explode=None, labels=None, colors=None, autopct=None, pctdistance=0.6, shadow=False, startangle=None, radius=None, counterclock=True, wedgeprops=None, textprops=None, center=(0, 0), frame=False, rotatelabels=False, normalize=True, **kwargs) 或 ax.pie(...)。
x: 扇形的大小数据(数值序列)。explode: 一个与x长度相同的序列,用于指定每个扇形偏离圆心的距离,从而突出显示某些部分。labels: 每个扇形的标签列表。colors: 每个扇形的颜色列表。autopct: 用于格式化显示百分比的字符串或函数。例如'%1.1f%%'表示保留一位小数的百分比。pctdistance: 百分比文本标签相对于圆心的距离比例(0到1之间)。shadow: 布尔值,如果为True,则显示阴影效果。startangle: 第一个扇形的起始角度(逆时针,默认为 0 度,即从 X 轴正方向开始)。radius: 饼图的半径。wedgeprops: 扇形楔形部分的属性字典,例如wedgeprops=dict(width=0.4, edgecolor='w')可以创建甜甜圈图。textprops: 标签文本的属性字典。
一般饼图: 直接使用 plt.pie() 绘制,通过 explode, labels, autopct 等参数进行定制。
嵌套饼图 (Nested Pie Chart): 通过绘制两个或多个饼图,并调整它们的 radius 和 wedgeprops 参数,可以创建同心圆的嵌套饼图,用于展示层次结构数据。通常内圈表示大类别,外圈表示子类别。
甜甜圈图 (Donut Chart): 甜甜圈图是饼图的一种变体,中间有一个空心。这可以通过 wedgeprops 中的 width 参数来实现,例如 wedgeprops=dict(width=0.4) 表示扇形的宽度为半径的 0.4 倍,中间留下 0.6 倍半径的空心。
7.1 一般饼图
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
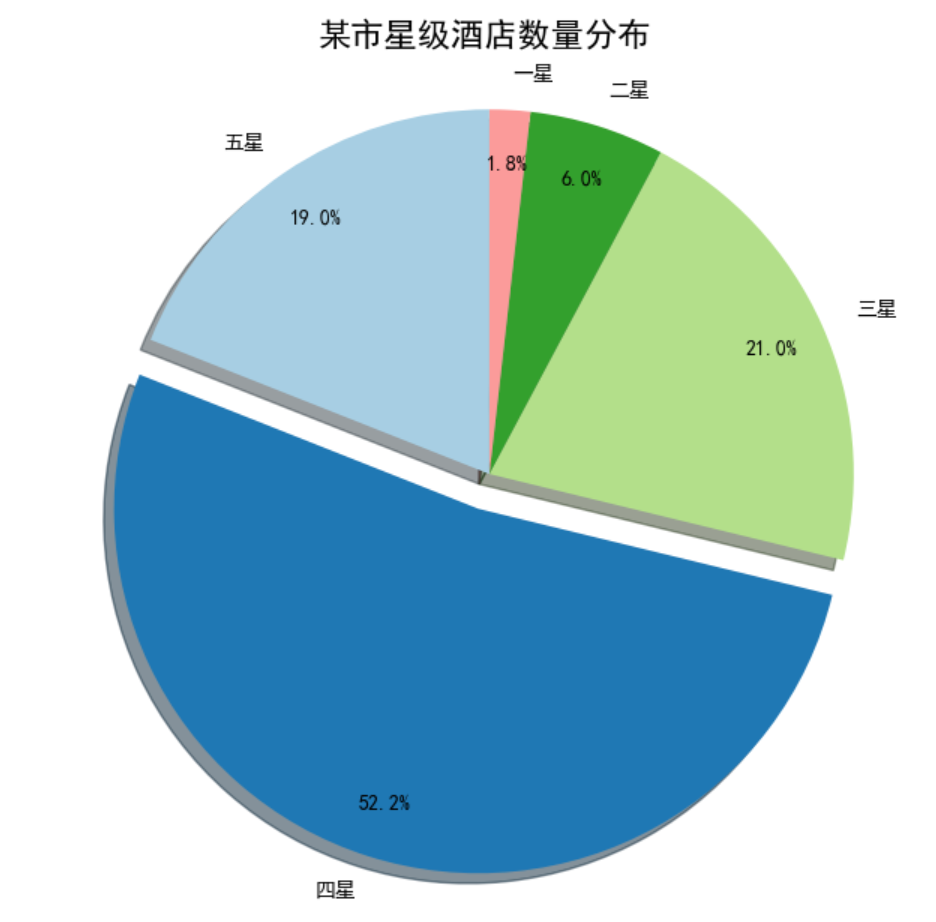
labels_pie = ["五星", "四星", "三星", "二星", "一星"]
percent_pie = [95, 261, 105, 30, 9] # 某市星级酒店数量
plt.figure(figsize=(7, 7), dpi=100)
# 偏移中心量,突出一部分
explode_pie = (0, 0.1, 0, 0, 0) # 为了突出四星级酒店
# 绘制饼图
plt.pie(
x=percent_pie,
explode=explode_pie,
labels=labels_pie,
colors=plt.cm.Paired.colors, # 颜色映射
autopct="%1.1f%%", # 保留一位小数的百分比
pctdistance=0.85, # 百分比文本距离圆心的比例
shadow=True,
startangle=90 # 从90度开始绘制第一个扇形
)
plt.title("某市星级酒店数量分布", pad=20, fontsize=16)
plt.axis("equal") # 确保饼图是圆形
plt.show()
7.2 嵌套饼图
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
import pandas as pd
import matplotlib.pyplot as plt
# 模拟数据
data = {
'type': ['水果', '水果', '蔬菜', '蔬菜', '肉类', '肉类', '谷物'],
'食材': ['苹果', '香蕉', '白菜', '胡萝卜', '猪肉', '牛肉', '大米'],
'花费': [50, 30, 20, 25, 80, 70, 40]
}
food = pd.DataFrame(data)
# --- 关键的修复步骤 ---
# 1. 明确定义内部饼图的顺序
# 这里我们仍然需要一个逻辑顺序来对齐内外层,即使颜色是自动的。
# 例如,我们可以根据类型名称的字母顺序,或者数据框中第一次出现的顺序。
# 为了确保内外层对应,最可靠的方法是先对数据进行排序。
# 这里我们沿用之前的逻辑,先按类型排序,这样同一类型的食材会聚集在一起。
food_sorted = food.sort_values(by=['type', '花费'], ascending=[True, False])
# 分组聚合,内圈数据(按照类型)
inner_data = food_sorted.groupby(by="type")["花费"].sum()
# 确保 inner_data 的索引顺序与 food_sorted 中 type 出现的顺序一致
# (groupby 默认会排序,所以这里可以省略 reindex,但显式写出更清晰)
inner_data = inner_data.reindex(food_sorted['type'].unique())
# 外圈数据(按照食材)
outer_data = food_sorted["花费"]
outer_labels = food_sorted["食材"]
plt.rcParams["font.size"] = 12
plt.figure(figsize=(10, 8)) # 调整图表大小以获得更好的显示效果
# 绘制内部饼图
# 使用 plt.cm.Set3.colors 作为内部饼图的颜色循环
wedges_inner, texts_inner, autotexts_inner = plt.pie(
x = inner_data,
radius = 0.6,
wedgeprops=dict(lw=3, width=0.6, edgecolor="w"),
labels=inner_data.index,
labeldistance=0.7,
startangle=90,
colors=plt.cm.Set3.colors, # 让Matplotlib自动选择颜色
autopct="%1.1f%%"
)
# 调整内部百分比文本颜色
for autotext in autotexts_inner:
autotext.set_color("blue")
autotext.set_fontsize(10)
# 绘制外部饼图
# 使用 plt.cm.tab20.colors 作为外部饼图的颜色循环
wedges_outer, texts_outer, autotexts_outer = plt.pie(
x = outer_data,
radius = 1,
wedgeprops=dict(lw=3, width=0.3, edgecolor="k"),
labels=outer_labels, # 使用排序后的食材标签
labeldistance=1.05,
autopct="%1.1f%%",
pctdistance=0.85,
startangle=90,
colors=plt.cm.tab20.colors # 让Matplotlib自动选择颜色,通常tab20颜色更多,适合外层
)
# 调整外部百分比文本颜色
for autotext in autotexts_outer:
autotext.set_color("darkred")
autotext.set_fontsize(8)
plt.title("食物花费嵌套饼图", pad=20, fontsize=18)
plt.axis("equal") # 确保饼图是圆形
# 图例标题
# 此时图例颜色将根据 Matplotlib 自动分配的颜色来显示
plt.legend(inner_data.index, title="食物类型", loc="center left", bbox_to_anchor=(1, 0, 0.5, 1), fontsize=10)
plt.tight_layout()
plt.show()

7.3 甜甜圈图
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
plt.figure(figsize=(7, 7), dpi=400)
# 数据
recipe = ["225g 面粉",
"90g 糖",
"1个鸡蛋",
"60g 黄油",
"100ml 牛奶",
"1/2包酵母"]
data_donut = np.array([225, 90, 50, 60, 100, 5])
# 归一化
data_donut_norm = data_donut / data_donut.sum()
# 绘制甜甜圈图, 通过wedgeprops的width参数<radius参数创造空心
wedges, texts, autotexts = plt.pie(
data_donut_norm,
autopct="%1.1f%%",
pctdistance=0.85,
startangle=90,
radius=1.2,
wedgeprops=dict(width=0.4, edgecolor="w",lw=1), # 甜甜圈的关键:width<radius
colors=plt.cm.tab10.colors
)
# 调整百分比文本颜色和大小
for autotext in autotexts:
autotext.set_color("white")
autotext.set_fontsize(10)
# 添加注释和箭头指向每个扇形
bbox_props = dict(boxstyle="round, pad=0.3", fc="w", ec="k", lw=0.72)
kw = dict(arrowprops=dict(arrowstyle="-"), bbox=bbox_props, va="center")
for i, p in enumerate(wedges):
ang = (p.theta2 - p.theta1) / 2. + p.theta1 # 计算扇形中心角度
y = np.sin(np.deg2rad(ang))
x = np.cos(np.deg2rad(ang))
# 根据x坐标判断文本水平对齐方式,使其位于扇形外侧
ha={-1:"right", 1:"left"}[int(np.sign(x))]
# 箭头连接样式, 从扇形中心指向文本
connectionstyle=f"angle, angleA=0, angleB={ang}"
kw["arrowprops"].update({"connectionstyle":connectionstyle})
# xytext的位置需要根据x, y符号调整,确保文本在甜甜圈外侧
# 1.4 * np.sign(x), 1.4*y确保文本在外部
plt.annotate(
recipe[i],
xy = (x * 1.05, y * 1.05),
xytext=(1.4 * np.sign(x), 1.4*y),
ha=ha,
fontsize=10,
weight="bold",
**kw
)
plt.title("甜甜圈图---->")
plt.axis("equal")
plt.tight_layout()
plt.show()
如果希望图片更加清晰,可以调整dpi参数.

选择题
-
在
plt.pie()函数中,哪个参数用于设置饼图中间的空心,从而创建甜甜圈图?A.
radiusB.width(在wedgeprops中) C.explodeD.pctdistance答案:B,
wedgeprops=dict(width=...)可以控制扇形的宽度,当宽度小于半径时,中间就会形成空心。 -
如果饼图中有多个类别,并且希望突出显示其中一个类别,应该调整哪个参数? A.
labelsB.colorsC.explodeD.autopct答案:C,
explode参数是一个与数据长度相同的序列,通过指定非零值,可以将对应的扇形从圆心拉出,达到突出显示的效果。
编程题
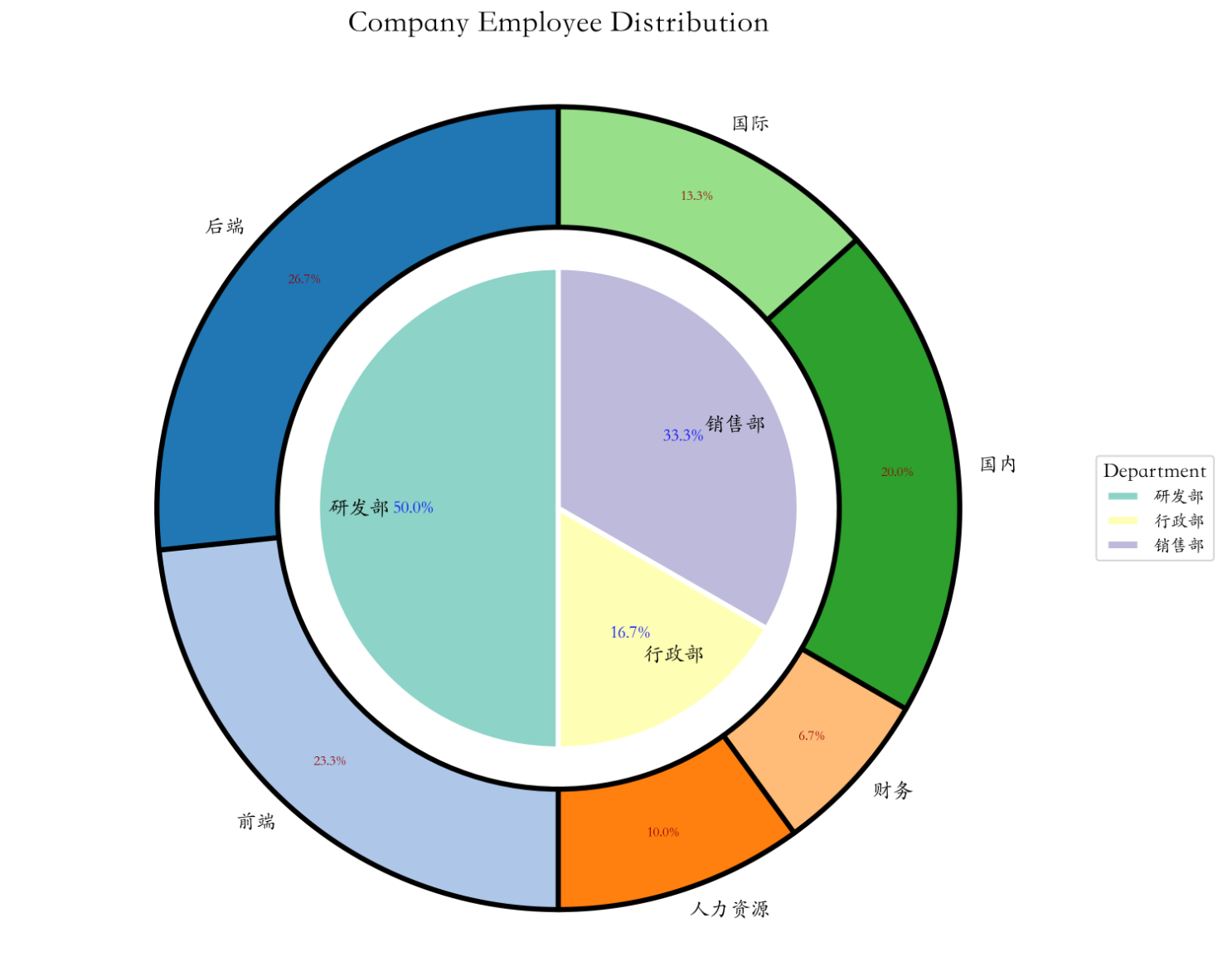
- 绘制一个嵌套饼图,展示一个公司的部门结构和员工分布。
- 内圈: 部门类别和员工总数。
- 研发部: 150 人
- 销售部: 100 人
- 行政部: 50 人
- 外圈: 各部门内部的子类别和员工数量。
- 研发部: 前端 (70), 后端 (80)
- 销售部: 国内 (60), 国际 (40)
- 行政部: 人力资源 (30), 财务 (20)
- 内圈和外圈使用不同的颜色映射。
- 显示百分比,保留一位小数。
- 添加标题 “Company Employee Distribution”。
- 为内圈添加图例,标题为 “Department”。
- 内圈: 部门类别和员工总数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
import pandas as pd
import matplotlib.pyplot as plt
# 模拟数据
data = {
'type': ['研发部', '研发部', '销售部', '销售部', '行政部', '行政部'],
'子类别': ['前端', '后端', '国内', '国际', '人力资源', '财务'],
'员工人数': [70, 80, 60, 40, 30, 20]
}
food = pd.DataFrame(data)
# --- 关键的修复步骤 ---
# 1. 明确定义内部饼图的顺序
# 这里我们仍然需要一个逻辑顺序来对齐内外层,即使颜色是自动的。
# 例如,我们可以根据类型名称的字母顺序,或者数据框中第一次出现的顺序。
# 为了确保内外层对应,最可靠的方法是先对数据进行排序。
# 这里我们沿用之前的逻辑,先按类型排序,这样同一类型的食材会聚集在一起。
food_sorted = food.sort_values(by=['type', '员工人数'], ascending=[True, False])
# 分组聚合,内圈数据(按照类型)
inner_data = food_sorted.groupby(by="type")["员工人数"].sum()
# 确保 inner_data 的索引顺序与 food_sorted 中 type 出现的顺序一致
# (groupby 默认会排序,所以这里可以省略 reindex,但显式写出更清晰)
inner_data = inner_data.reindex(food_sorted['type'].unique())
# 外圈数据(按照食材)
outer_data = food_sorted["员工人数"]
outer_labels = food_sorted["子类别"]
plt.rcParams["font.size"] = 12
plt.figure(figsize=(10, 8), dpi=300) # 调整图表大小以获得更好的显示效果
# 绘制内部饼图
# 使用 plt.cm.Set3.colors 作为内部饼图的颜色循环
wedges_inner, texts_inner, autotexts_inner = plt.pie(
x = inner_data,
radius = 0.6,
wedgeprops=dict(lw=3, width=0.6, edgecolor="w"),
labels=inner_data.index,
labeldistance=0.7,
startangle=90,
colors=plt.cm.Set3.colors, # 让Matplotlib自动选择颜色
autopct="%1.1f%%"
)
# 调整内部百分比文本颜色
for autotext in autotexts_inner:
autotext.set_color("blue")
autotext.set_fontsize(10)
# 绘制外部饼图
# 使用 plt.cm.tab20.colors 作为外部饼图的颜色循环
wedges_outer, texts_outer, autotexts_outer = plt.pie(
x = outer_data,
radius = 1,
wedgeprops=dict(lw=3, width=0.3, edgecolor="k"),
labels=outer_labels, # 使用排序后的食材标签
labeldistance=1.05,
autopct="%1.1f%%",
pctdistance=0.85,
startangle=90,
colors=plt.cm.tab20.colors # 让Matplotlib自动选择颜色,通常tab20颜色更多,适合外层
)
# 调整外部百分比文本颜色
for autotext in autotexts_outer:
autotext.set_color("darkred")
autotext.set_fontsize(8)
plt.title("Company Employee Distribution", pad=20, fontsize=18)
plt.axis("equal") # 确保饼图是圆形
# 图例标题
# 此时图例颜色将根据 Matplotlib 自动分配的颜色来显示
plt.legend(inner_data.index, title="Department", loc="center left", bbox_to_anchor=(1, 0, 0.5, 1), fontsize=10)
plt.tight_layout()
plt.show()
如果想要调整图片清晰度,可以调整dpi参数:
8.热力图 (Heatmap)
热力图是一种通过颜色深浅来表示数据矩阵中数值大小的图表。它常用于可视化相关性矩阵、混淆矩阵或任何二维网格数据。
主要函数是 plt.imshow(X, cmap=None, norm=None, aspect=None, interpolation=None, alpha=None, vmin=None, vmax=None, origin=None, extent=None, filternorm=1, filterrad=4.0, resample=None, **kwargs) 或 ax.imshow(...)。
X: 要可视化的二维数组(矩阵)。cmap: 颜色映射 (Colormap) 对象或名称(例如'viridis','hot','cool','RdBu')。norm: 用于将数据值归一化到颜色映射范围(通常是 0 到 1)的Normalize对象。aspect: 图像的宽高比。'auto'(默认) 自动调整,'equal'保持像素的方形。interpolation: 图像插值方法(例如'nearest','bilinear','bicubic')。alpha: 图像的透明度。vmin,vmax: 颜色映射的数据范围。origin: 图像的原点位置('upper'(默认) 或'lower')。extent: 图像的 X 和 Y 轴数据范围(left, right, bottom, top)。
热力图通常与 plt.colorbar() 结合使用,以解释颜色与数值的对应关系。
在热力图上添加文本: 可以通过嵌套循环遍历数据矩阵的每个单元格,然后使用 ax.text() 在每个单元格的中心位置添加对应的数值文本。
下面这个例子就展示了混淆矩阵:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
from sklearn.metrics import confusion_matrix
import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np
# 模拟真实标签和预测标签
y_true = np.array([0, 1, 2, 0, 1, 2, 0, 1, 2, 0, 0, 1, 1, 2, 2])
y_pred = np.array([0, 1, 1, 0, 2, 2, 0, 0, 2, 1, 0, 1, 1, 2, 1])
# 计算混淆矩阵
cm = confusion_matrix(y_true, y_pred)
class_names = ['Class 0', 'Class 1', 'Class 2']
plt.figure(figsize=(8, 6))
sns.heatmap(cm, annot=True, fmt='d', cmap='Blues', cbar=True,
xticklabels=class_names, yticklabels=class_names,
linewidths=.5, linecolor='black')
plt.xlabel('Predicted Label')
plt.ylabel('True Label')
plt.title('Confusion Matrix', fontsize=16)
plt.show()

例子:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
# 准备数据:
vegetables = ["黄瓜", "番茄", "生菜", "芦笋", "土豆", "小麦", "大麦"]
farmers = ['农民A', '农民B', '农民C', '农民D', '农民E', '农民F', '农民G']
# 模拟农民丰收的数据
harvest = np.random.rand(len(vegetables), len(farmers)) # 7*7的矩阵(方阵)
plt.figure(figsize=(10, 10))
# 绘制热力图
# cmap="YIGnBu"是一个从浅黄到深绿蓝的颜色映射
# `origin`: 图像的原点位置(`'upper'` (默认) 或 `'lower'`)。
# `aspect`: 图像的宽高比。`'auto'` (默认) 自动调整,`'equal'` 保持像素的方形。
im = plt.imshow(harvest, cmap="YlGnBu", origin="upper", aspect="auto")
# 设置X轴和Y轴的刻度标签
plt.xticks(np.arange(len(farmers)), farmers, rotation=45, ha="right", fontsize=12)
plt.yticks(np.arange(len(vegetables)), vegetables, fontsize=12)
# 绘制每个单元格的数值文本
for i in range(len(vegetables)):
for j in range(len(farmers)):
text = plt.text(
j,i,
f"{harvest[i, j]:.1f}",
ha="center",
va="center",
color="k",
fontsize=9,
weight="bold"
)
# 添加颜色条和标题
plt.title("本地农民农作物收成(吨/年)", pad=20, fontsize=18)
cbar = plt.colorbar(im, fraction=0.046, pad=0.04)
cbar.set_label("收成(吨)", rotation=270, labelpad=15, fontsize=12)
plt.tight_layout()
plt.show()

选择题
-
在
plt.imshow(X, ...)中,X参数通常是什么类型的数据? A. 一维数组 B. 二维数组(矩阵) C. 字符串 D. 列表答案:B,
imshow用于显示图像或二维数据,因此X必须是二维数组。 -
要为热力图添加一个解释颜色与数值对应关系的图例,应该使用哪个函数?
A.
plt.legend()B.plt.colorbar()C.plt.text()D.plt.title()答案:B,
plt.colorbar()用于创建颜色条,它与imshow或其他使用颜色映射的函数结合使用。
编程题
- 创建一个 5x5 的随机整数矩阵,数值范围在 1 到 100 之间。
- 绘制这个矩阵的热力图。
- 使用
'hot'颜色映射。 - 显示每个单元格的数值。
- 添加标题 “Random 5x5 Matrix Heatmap”。
- 添加 X 轴和 Y 轴标签,分别为 “Column Index” 和 “Row Index”。
- 添加颜色条,标签为 “Value”。
- 使用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
plt.figure(figsize=(7, 7), dpi=300)
m = np.random.randint(1, 101, size=(5, 5))
im = plt.imshow(m, cmap="hot", origin="upper", aspect="auto")
# 绘制每个单元格的数值文本
for i in range(5):
for j in range(5):
text = plt.text(
j,i,
f"{m[i, j]:.1f}",
ha="center",
va="center",
color="blue",
fontsize=9,
weight="bold"
)
plt.title("Random 5x5 Matrix Heatmap", pad=20, fontsize=18)
plt.xlabel("Column Index")
plt.ylabel("Row Index")
# 添加颜色条和标题
cbar = plt.colorbar(im, fraction=0.046, pad=0.04)
cbar.set_label("Value", rotation=270, labelpad=15, fontsize=12)
plt.tight_layout()
plt.show()

9.面积图 (Area Plot)
面积图是一种特殊的折线图,它通过填充曲线下方的区域来表示数值。当有多条曲线时,面积图可以是堆叠的,用于显示各部分随时间或类别变化的构成。
主要函数是 plt.stackplot(x, *args, labels=None, colors=None, baseline='zero', **kwargs) 或 ax.stackplot(...)。
x: X 轴数据(通常是时间或有序类别)。*args: 要堆叠的 Y 轴数据序列。每个序列代表一个层。labels: 每个层的标签列表,用于图例。colors: 每个层的颜色列表。baseline: 堆叠的基线类型。'zero'(默认): 从 Y=0 开始堆叠。'sym'(symmetric): 堆叠在 Y=0 的两侧对称。'wiggle': 最小化层之间的平方斜率。'weighted_wiggle': 最小化加权平方斜率。
面积图特别适合展示“部分到整体”的关系随时间的变化。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# 1. 准备数据
days = np.arange(1, 6) # 5天
sleeping = [7, 8, 6, 11, 7] # 睡眠时间
eating = [2, 3, 4, 3, 2] # 吃饭时间
working = [7, 8, 7, 2, 2] # 工作时间
playing = [8, 5, 7, 8, 13] # 娱乐时间
plt.figure(figsize=(10, 7))
# 绘制堆叠面积图
plt.stackplot(
days,
sleeping,
eating,
working,
playing,
labels=['Sleeping', 'Eating', 'Working', 'Playing'], # 每个层的标签
colors=['#6d904f', '#fc4f30', '#008fd5', '#e5ae38'], # 自定义颜色
alpha=0.8 # 透明度
)
plt.xlabel('Day of the Week', fontsize=12)
plt.ylabel('Hours Spent', fontsize=12)
plt.title('Daily Activities Stack Plot', fontsize=16)
plt.legend(loc="upper left", fontsize=10)
plt.grid(True, ls=":", alpha=0.7)
plt.show()

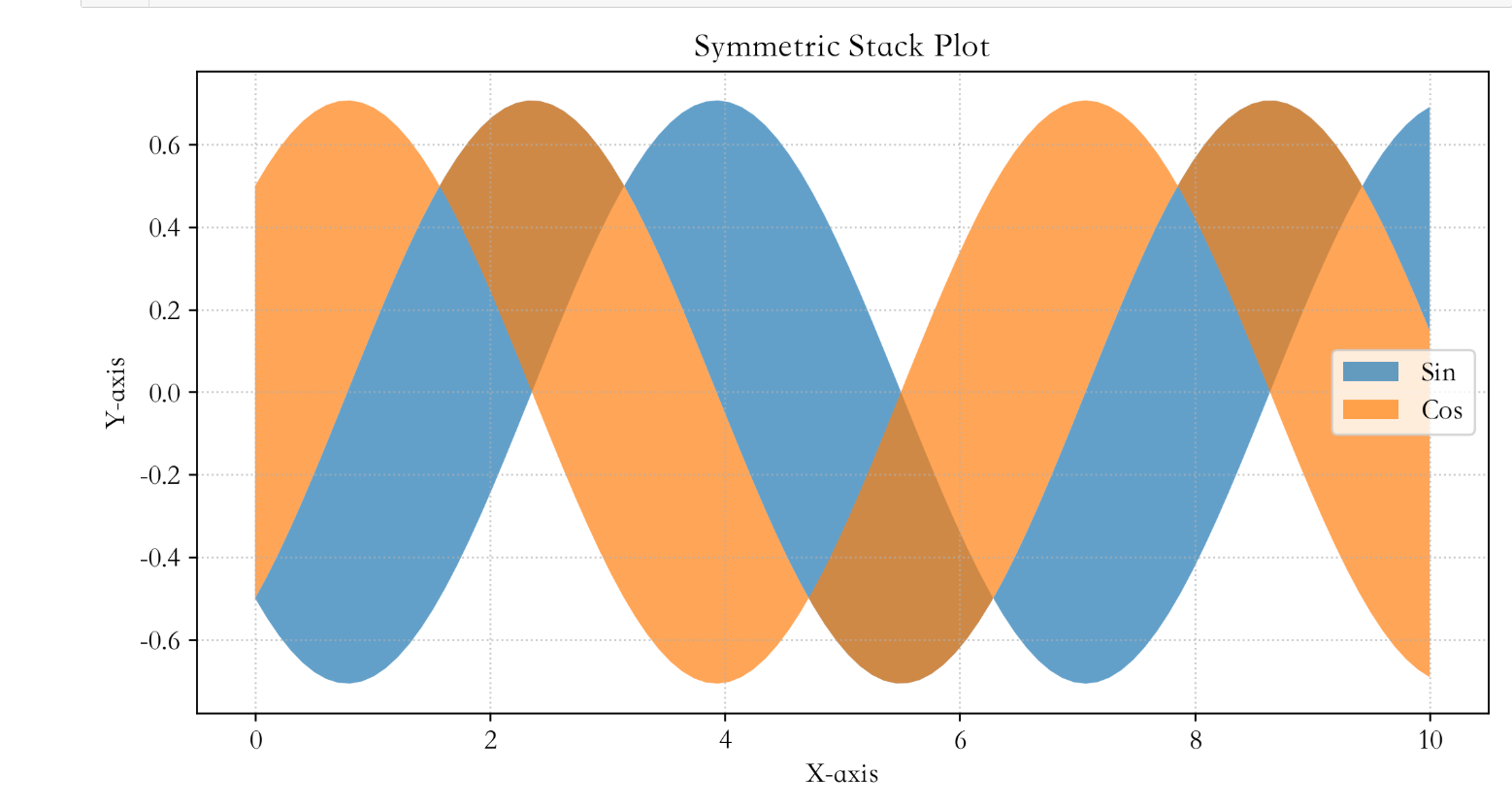
拓展:不同基线的面积图
1
2
3
4
5
6
7
8
9
10
11
12
13
14
x_base = np.linspace(0, 10, 100)
y1_base = np.sin(x_base)
y2_base = np.cos(x_base)
plt.figure(figsize=(10, 5), dpi=250)
# baseline="sym" 堆叠在 Y=0 的两侧对称
plt.stackplot(x_base, y1_base, y2_base, labels=["Sin", "Cos"], alpha=0.7, baseline="sym")
plt.title('Symmetric Stack Plot')
plt.xlabel('X-axis')
plt.ylabel('Y-axis')
plt.legend()
plt.grid(True, linestyle=':', alpha=0.7)
plt.show()
选择题
-
面积图主要用于展示什么?
A. 两个变量之间的相关性。 B. 各部分在整体中的构成随时间的变化。 C. 数据点的分布情况。 D. 数据的中位数和四分位数。
答案:B,面积图通过堆叠不同部分的面积来展示整体构成随时间或有序类别的变化。
-
在
plt.stackplot()中,哪个参数用于指定堆叠的起始基线? A.labelsB.colorsC.baselineD.alpha答案:C,
baseline参数决定了堆叠的起始基线,例如'zero'从 Y=0 开始。baseline: 堆叠的基线类型。'zero'(默认): 从 Y=0 开始堆叠。'sym'(symmetric): 堆叠在 Y=0 的两侧对称。'wiggle': 最小化层之间的平方斜率。'weighted_wiggle': 最小化加权平方斜率。
编程题
- 模拟一个网站在 7 天内的不同流量来源(”Direct”, “Search Engine”, “Social Media”)。
- Direct 流量:
[50, 60, 55, 70, 80, 75, 90] - Search Engine 流量:
[30, 40, 45, 50, 60, 65, 70] - Social Media 流量:
[20, 25, 30, 35, 40, 45, 50]
- Direct 流量:
- 绘制这些流量来源的堆叠面积图。
- X 轴为天数 (1到7)。
- 为每个流量来源指定不同的颜色。
- 添加标题 “Website Traffic Sources Over 7 Days”。
- 添加 X 轴标签 “Day” 和 Y 轴标签 “Traffic Count”。
- 显示图例。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# 1. 准备数据
days = np.arange(1, 8) # 7天
direct = [50, 60, 55, 70, 80, 75, 90]
search_engine = [30, 40, 45, 50, 60, 65, 70]
social_media = [20, 25, 30, 35, 40, 45, 50]
plt.figure(figsize=(10, 7))
# 绘制堆叠面积图
plt.stackplot(
days,
direct,
search_engine,
social_media,
labels=['direct', 'Search Engine', 'Social Media'], # 每个层的标签
colors=['#6d904f', '#fc4f30', '#008fd5'], # 自定义颜色
alpha=0.8 # 透明度
)
plt.xlabel('Day', fontsize=12)
plt.ylabel('Traffic Count', fontsize=12)
plt.title('Website Traffic Sources Over 7 Days', fontsize=16)
plt.legend(loc="upper left", fontsize=10)
plt.grid(True, ls=":", alpha=0.7)
plt.show()

10.蜘蛛图 (Radar Chart / Spider Plot)
蜘蛛图(又称雷达图)是一种多变量图表,用于比较多个实体在多个定量变量上的表现。它将每个变量表示为从中心点向外辐射的轴,数据点沿着这些轴绘制并连接起来,形成一个多边形。
创建蜘蛛图的关键是使用极坐标投影 projection='polar',然后设置角度刻度标签和径向刻度。
主要步骤:
- 数据准备:
labels: 维度标签(例如,技能名称、属性)。stats: 每个维度上的数值。angles: 计算每个维度在极坐标系中的角度。通常将 2pi 平分为len(labels)份。为了闭合多边形,需要将第一个数据点和角度复制到末尾。
- 创建极坐标 Axes:
fig.add_subplot(111, polar=True)。 - 绘制多边形:
ax.plot(angles, stats, 'o-', linewidth=2): 绘制连接数据点的折线。ax.fill(angles, stats, alpha=0.25): 填充多边形区域。
- 设置刻度:
ax.set_thetagrids(angles * 180 / np.pi, labels): 设置角度轴的刻度位置和标签。angles * 180 / np.pi将弧度转换为度数。ax.set_rgrids(radii_ticks): 设置径向轴的刻度位置。ax.set_ylim(min_val, max_val): 设置径向轴的显示范围。
- 标题:
ax.set_title(...)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
# 1. 准备数据
labels = np.array(["个人能力", "IQ", "服务意识", "团队精神", "解决问题能力", "持续学习"])
stats_person1 = [83, 61, 95, 67, 76, 88] # 某人的能力得分
stats_person2 = [70, 85, 75, 90, 80, 70] # 另一个人或团队的能力得分
# 2. 画图数据准备:计算角度
num_vars = len(labels)
angles = np.linspace(0, 2 * np.pi, num_vars, endpoint=False).tolist() # 角度列表
# 为了闭合图形,需要将第一个数据点和角度复制到末尾
stats_person1 = stats_person1 + stats_person1[:1]
stats_person2 = stats_person2 + stats_person2[:1]
angles = angles + angles[:1]
# 3. 用Matplotlib画蜘蛛图
fig = plt.figure(figsize=(9, 9), dpi=300)
ax = fig.add_subplot(111, polar=True) # 创建极坐标 Axes
# 绘制第一个人的数据
ax.plot(angles, stats_person1, 'o-', linewidth=2, color='blue', label='Person A') # 连线
ax.fill(angles, stats_person1, color='blue', alpha=0.25) # 填充
# 绘制第二个人的数据
ax.plot(angles, stats_person2, 'o-', linewidth=2, color='green', label='Person B') # 连线
ax.fill(angles, stats_person2, color='green', alpha=0.25) # 填充
# 4. 设置角度轴标签
ax.set_thetagrids(np.array(angles[:-1]) * 180 / np.pi, labels, fontsize=14) # 角度值和标签
# 5. 设置径向轴刻度
ax.set_rgrids([20, 40, 60, 80, 100], fontsize=12) # 半径刻度
ax.set_ylim(0, 100) # 设置径向轴范围 (0-100分)
# 6. 添加标题和图例
ax.set_title("个人能力雷达图对比", fontsize=18, pad=20)
ax.legend(loc='upper right', bbox_to_anchor=(1.2, 1.1), fontsize=12) # 调整图例位置
ax.grid(True, linestyle=':', alpha=0.7)
plt.tight_layout()
plt.show()

选择题
-
创建蜘蛛图时,需要将
Axes对象的projection参数设置为: A.'cartesian'B.'3d'C.'polar'D.'rectilinear'答案:C,蜘蛛图是基于极坐标系的。
-
在绘制蜘蛛图时,为了使多边形闭合,通常需要对数据和角度进行什么操作?
A. 将所有数据点乘以 2。
B. 将第一个数据点和角度复制到序列的末尾。
C. 将最后一个数据点和角度复制到序列的开头。
D. 对数据进行排序。
答案:B,这样做可以使绘制的折线从最后一个点连接回第一个点,从而形成闭合的多边形。
编程题
- 模拟两款手机在以下五个方面的评分(满分 10 分):
- 方面: “性能”, “拍照”, “续航”, “屏幕”, “价格”
- 手机 A 评分:
[8, 7, 9, 8, 6] - 手机 B 评分:
[7, 9, 7, 9, 8]
- 绘制这两款手机的蜘蛛图。
- 手机 A 的线条颜色为蓝色,填充颜色为浅蓝色。
- 手机 B 的线条颜色为绿色,填充颜色为浅绿色。
- 设置径向轴范围为 0 到 10。
- 添加标题 “Smartphone Comparison Radar Chart”。
- 显示图例。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
# 1. 准备数据
labels = np.array(["性能", "拍照", "续航", "屏幕", "价格"])
stats_A = [8, 7, 9, 8, 6]
stats_B = [7, 9, 7, 9, 8]
# 2. 画图数据准备:计算角度
num_vars = len(labels)
angles = np.linspace(0, 2 * np.pi, num_vars, endpoint=False).tolist() # 角度列表
# 为了闭合图形,需要将第一个数据点和角度复制到末尾
stats_A = stats_A + stats_A[:1]
stats_B = stats_B + stats_B[:1]
angles = angles + angles[:1]
# 3. 用Matplotlib画蜘蛛图
fig = plt.figure(figsize=(9, 9), dpi=300)
ax = fig.add_subplot(111, polar=True) # 创建极坐标 Axes
# 绘制第一个人的数据
ax.plot(angles, stats_A, 'o-', linewidth=2, color='blue', label='手机A') # 连线
ax.fill(angles, stats_A, color='lightblue', alpha=0.25) # 填充
# 绘制第二个人的数据
ax.plot(angles, stats_B, 'o-', linewidth=2, color='green', label='手机B') # 连线
ax.fill(angles, stats_B, color='lightgreen', alpha=0.25) # 填充
# 4. 设置角度轴标签
ax.set_thetagrids(np.array(angles[:-1]) * 180 / np.pi, labels, fontsize=14) # 角度值和标签
# 5. 设置径向轴刻度
ax.set_rgrids([2, 4, 6, 8, 10], fontsize=12) # 半径刻度
ax.set_ylim(0, 10) # 设置径向轴范围 (0-100分)
# 6. 添加标题和图例
ax.set_title("Smartphone Comparison Radar Chart", fontsize=18, pad=20)
ax.legend(loc='upper right', bbox_to_anchor=(1.2, 1.1), fontsize=12) # 调整图例位置
ax.grid(True, linestyle=':', alpha=0.7)
plt.tight_layout()
plt.show()
