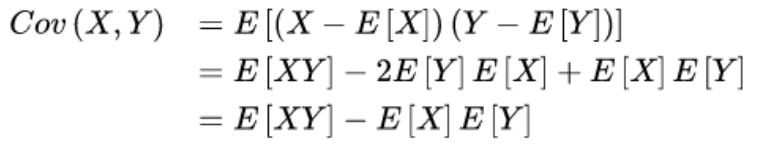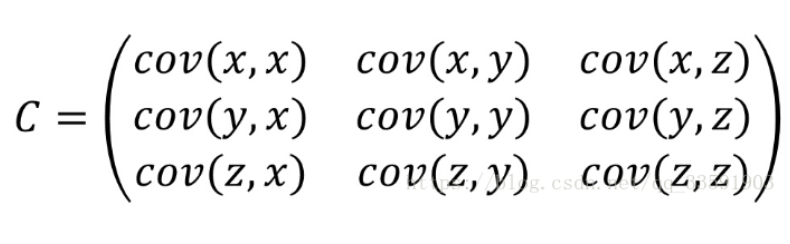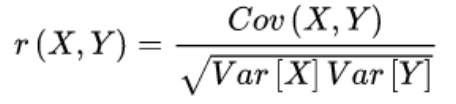pandas 库不仅提供了强大的数据结构,还内置了丰富的数学和统计方法,以及灵活的数据处理和分析工具。这些功能使得数据汇总、探索、清洗和特征工程变得高效且直观。
pandas 对象(Series 和 DataFrame)拥有一组常用的数学和统计方法,它们属于汇总统计(summary statistics)。这些方法可以对 Series 进行汇总计算(如求均值、最大值),或者对 DataFrame 的行或列进行汇总计算,并返回一个 Series 或 DataFrame。
1.简单统计指标
这些方法用于计算数据集中最基本的统计量,帮助我们快速了解数据的中心趋势、离散程度和范围。
df.count(axis=0, level=None, numeric_only=False):- 计算非
NA(非缺失)值的数量。 axis: 默认为0(按列计算),也可以设置为1(按行计算)。numeric_only: 仅计算数值列。
- 计算非
df.max(axis=0, skipna=True, level=None):- 计算最大值。
skipna: 默认为True,表示在计算时跳过NA值。
df.min(axis=0, skipna=True, level=None):- 计算最小值。
df.median(axis=0, skipna=True, level=None):- 计算中位数(数据的中间值)。
df.sum(axis=0, skipna=True, level=None):- 计算总和。
df.mean(axis=0, skipna=True, level=None):- 计算算术平均值。
df.quantile(q=0.5, axis=0, numeric_only=True):- 计算分位数。
q可以是单个浮点数(0到1之间)或浮点数列表。例如,q=0.5是中位数,q=[0.25, 0.75]是四分位数。
- 计算分位数。
df.describe(percentiles=None, include=None, exclude=None):- 生成数值型列的汇总统计信息,包括非
NA计数、平均值、标准差、最小值、四分位数(25%、50%、75%)和最大值。 - 对于非数值型(如对象或分类)列,它会显示计数、唯一值数量和出现频率最高的项。
- 生成数值型列的汇总统计信息,包括非
pandas的这些统计方法在底层依赖于NumPy的高度优化实现。它们通过矢量化操作,直接在 C 语言层面执行计算,从而避免了 Python 循环的开销,确保了在大数据集上的高性能。
axis参数: 决定了计算是沿着行进行(axis=1,对每行求统计量)还是沿着列进行(axis=0,对每列求统计量)。skipna参数: 这些函数默认会跳过NaN值。这意味着在计算均值、总和等时,NaN值不会被包含在计算中,也不会导致结果为NaN(除非所有值都是NaN)。describe()的原理:describe()方法会根据列的数据类型,自动选择合适的统计量进行计算。对于数值列,它会调用count(),mean(),std(),min(),quantile(),max()等内部方法。
level 参数与多层索引
当 DataFrame 具有多层索引(MultiIndex)时,这些统计方法还可以使用 level 参数,对指定索引级别的数据进行分组聚合。例如,df.mean(level='Student_ID') 可以计算每个学生的平均分,即使数据是按学生和科目分层的。
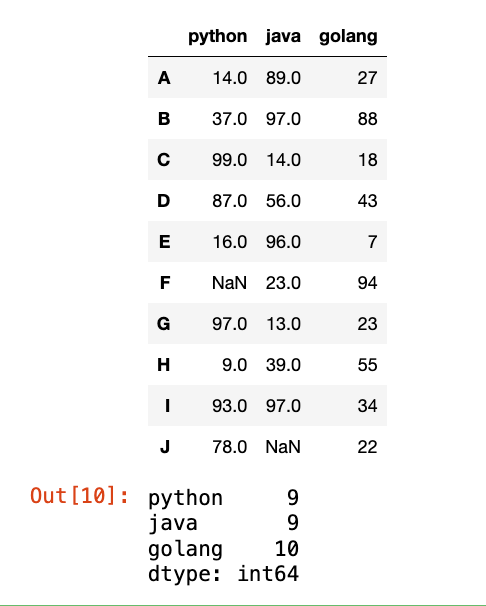
【1】非NaN的数量:
1
2
3
4
5
6
data = np.random.randint(0, 101, (10, 3))
df = pd.DataFrame(data=data, index=list("ABCDEFGHIJ"), columns=["python", "java", "golang"])
df.iloc[5, 0] = np.nan
df.iloc[9, 1] = np.nan
display(df)
df.count()
【2】轴0 的最大值:
1
df.max(axis=0)
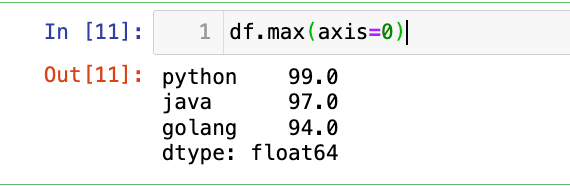
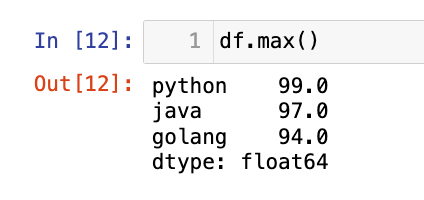
不加axis=0也可以,因为是默认的:
1
df.max()
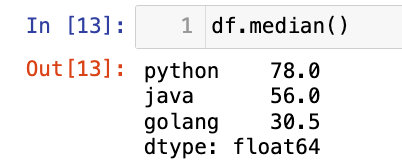
【3】中位数:
1
df.median()
【4】求和:
1
df.sum()
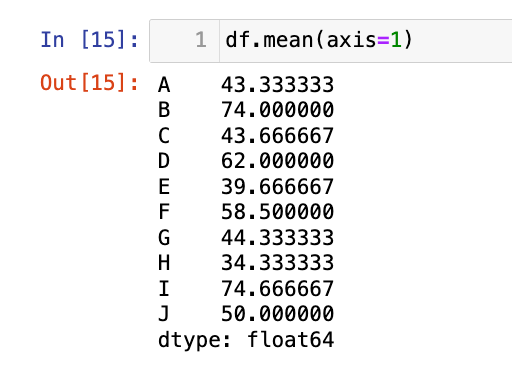
【5】每行的均值:(轴1的均值)
1
df.mean(axis=1)
【6】分位数:
1
df.quantile(q=[0.2, 0.4, 0.8])

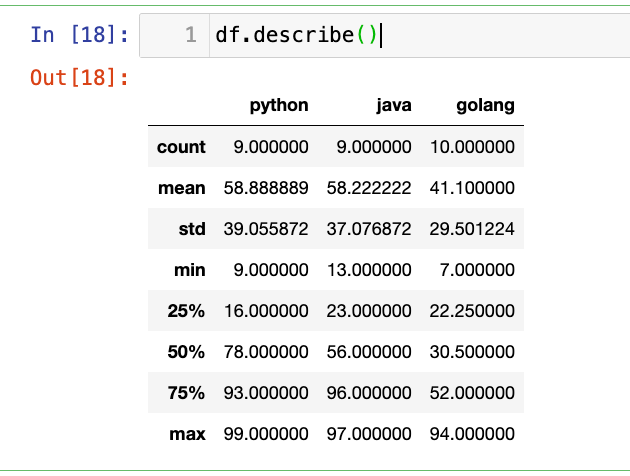
【7】查看数值型列的汇总统计:
1
df.describe()
【8】有MultiIndex时使用level参数:
1
2
3
4
5
data = np.random.randint(0, 100, (6, 2))
index = pd.MultiIndex.from_product([["A", "B", "C"], ["Q1", "Q2"]])
df_multi = pd.DataFrame(data=data, index=index, columns=["Sales", "Profit"])
display(df_multi)
df_multi["Sales"].groupby(level=-1).mean()
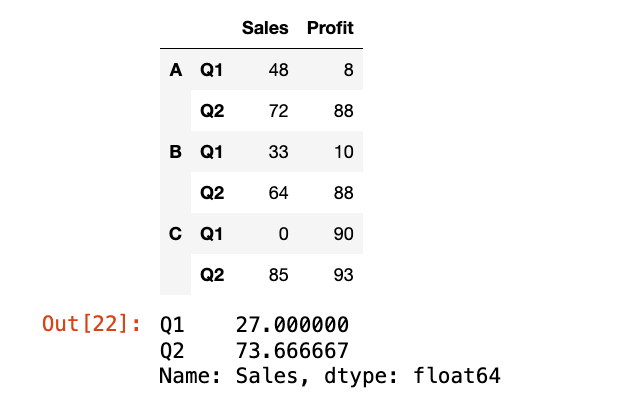
1
df_multi["Sales"].groupby(level=0).mean()

选择题
-
给定
s = pd.Series([1, 2, np.nan, 4]),执行s.count()的结果是什么?A. 4
B. 3
C. 2
D. 1
答案:B
-
以下哪个方法会返回 DataFrame 中所有数值型列的均值、标准差、最小值、四分位数和最大值?
A.
df.mean()B.
df.describe()C.
df.info()D.
df.sum()答案:B,
df.info(): 返回 DataFrame 的结构信息(如列名、数据类型、非空计数),不包含统计信息。
2.索引标签、位置获取
除了获取统计值本身,我们还经常需要找出这些统计值在数组中的位置(索引或标签)。
Series.argmin(axis=None, skipna=True):- 计算 Series 中最小值的整数位置(索引)。
- 如果 Series 中有多个最小值,返回第一个出现的最小值的位置。
Series.argmax(axis=None, skipna=True):- 计算 Series 中最大值的整数位置(索引)。
df.idxmax(axis=0, skipna=True):- 计算 DataFrame 中每个列(或行)的最大值对应的索引标签。
- 返回一个 Series,其索引是原始 DataFrame 的列名(或行索引),值是最大值所在的索引标签。
df.idxmin(axis=0, skipna=True):- 计算 DataFrame 中每个列(或行)的最小值对应的索引标签。
这些方法在底层会遍历 Series 或 DataFrame 的指定轴,比较元素值,并记录最大/最小值及其位置。
argmin()/argmax()返回的是基于 0 的整数位置,这与 NumPy 的argmin()/argmax()行为一致。idxmax()/idxmin()则更进一步,它们返回的是pandas索引对象中对应的标签。这在 DataFrame 具有非整数索引时特别有用,因为它直接提供了有意义的标签,而不是仅仅一个数字位置。
应用场景:
- 找出最佳/最差表现: 在销售数据中找出销售额最高的月份,或利润最低的产品。
- 时间序列分析: 找出历史数据中最高或最低点发生的时间戳。
- 数据清洗: 结合这些方法找出异常值所在的具体位置。
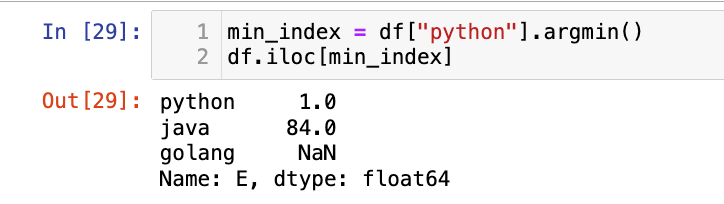
【1】某一列最小值的整数位置:
1
df["python"].argmin()
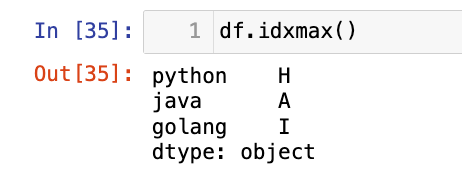
【2】每列最大值的索引标签:
1
df.idxmax()
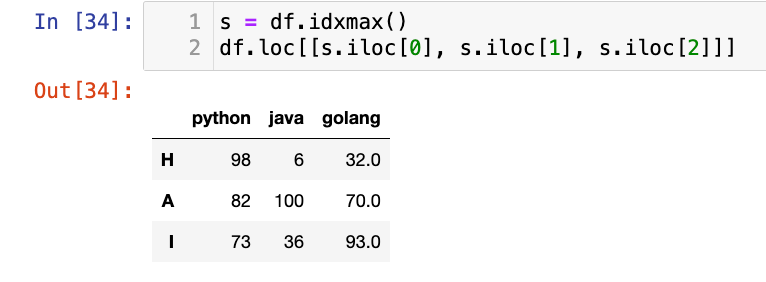
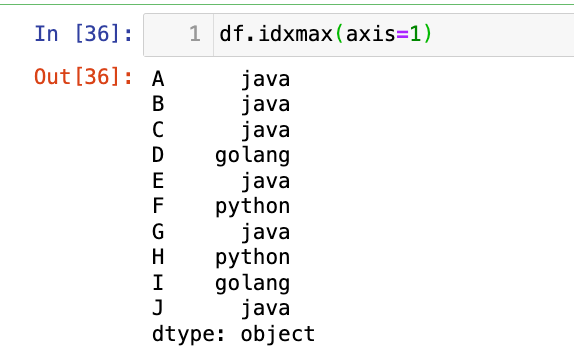
【3】行方向上查找最大值/最小值的标签
1
df.idxmax(axis=1)
选择题
-
给定
s = pd.Series([10, 5, 20], index=['a', 'b', 'c']),执行s.argmax()的结果是什么?A.
'c'B.2C.20D. 报错答案:B
-
以下哪个方法会返回 DataFrame 中每列最大值对应的索引标签?
A.
df.max()B.df.argmax()C.df.idxmax()D.df.loc[df.max()]答案:C
编程题
- 创建一个 DataFrame
product_ratings,包含'Product_ID'作为行索引,以及'Design_Score','Performance_Score'两列,填充随机整数评分(1到10)。 - 找出
'Design_Score'列中最高评分对应的产品 ID。 - 找出
'Performance_Score'列中最低评分对应的产品 ID。 - 找出每个产品(行)的最高评分是在哪个指标(列)上。
- 打印每一步操作后的结果。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
pro_id = np.arange(1, 11)
des_s = np.random.randint(1, 11, (10, ))
per_s = np.random.randint(1, 11, (10, ))
data = {"Product_ID": pro_id, "Design_Score": des_s, "Performance_Score": per_s}
product_ratings = pd.DataFrame(data=data)
display(product_ratings)
# 找出 'Design_Score' 列中最高评分对应的产品 ID
des_max = product_ratings.Product_ID[product_ratings["Design_Score"].argmax()]
print(des_max)
# 找出 'Performance_Score' 列中最低评分对应的产品 ID
per_min = product_ratings.Product_ID[product_ratings["Performance_Score"].argmin()]
print(per_min)
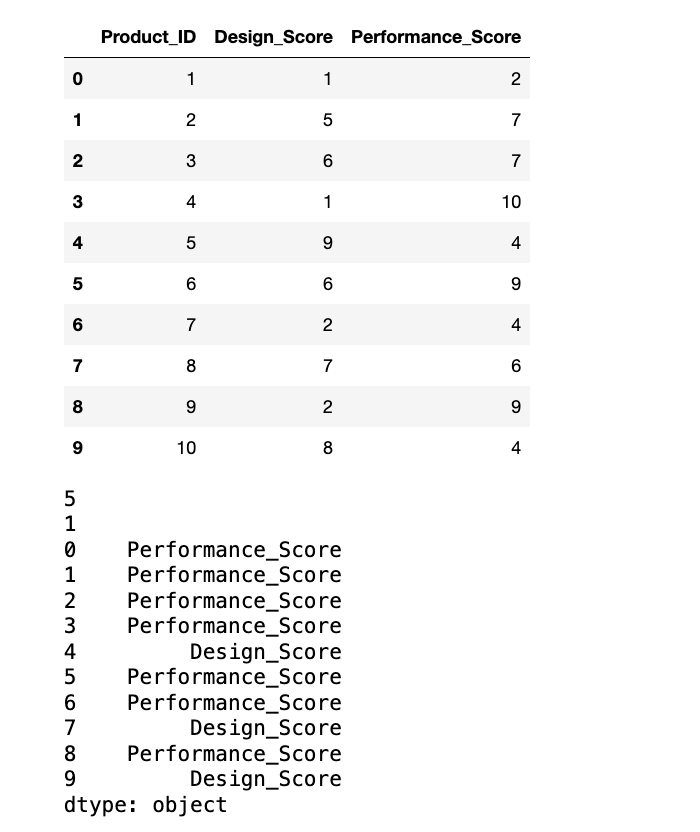
# 找出每个产品(行)的最高评分是在哪个指标(列)上。
max_ = product_ratings.loc[:, ["Design_Score", "Performance_Score"]].idxmax(axis=1)
print(max_)
3.更多统计指标
除了简单的聚合统计,pandas 还提供了一些用于数据分布、变化和唯一性分析的统计方法。
Series.value_counts(normalize=False, sort=True, ascending=False, bins=None, dropna=True):- 统计 Series 中每个唯一值出现的次数。
normalize: 布尔值,如果为True,则返回相对频率(百分比)。sort: 布尔值,是否按频率降序排序。dropna: 布尔值,是否包含NaN值的计数。
Series.unique():- 返回 Series 中所有唯一值的 NumPy 数组(顺序与第一次出现时的顺序一致)。
df.cumsum(axis=0, skipna=True):- 计算累积和。
df.cumprod(axis=0, skipna=True):- 计算累积乘积。
df.std(axis=0, skipna=True, ddof=1):- 计算标准差。
ddof是自由度,默认为1(样本标准差)。
- 计算标准差。
df.var(axis=0, skipna=True, ddof=1):- 计算方差。
df.cummin(axis=0, skipna=True):- 计算累积最小值。
df.cummax(axis=0, skipna=True):- 计算累积最大值。
df.diff(periods=1, axis=0):- 计算当前元素与前一个(或后一个)元素之间的差分。常用于时间序列分析。
periods: 整数,指定要计算的滞后(lag)期数。
df.pct_change(periods=1, axis=0):- 计算当前元素与前一个(或后一个)元素之间的百分比变化。常用于金融数据分析
value_counts()和unique(): 这些方法在底层使用哈希表来高效地识别和计数唯一元素。value_counts()会构建一个频率分布表。累积函数 (
cumsum,cumprod,cummin,cummax): 这些函数通过迭代 Series 或 DataFrame 的元素,并维护一个累积状态来实现。它们在底层是高度优化的,避免了显式循环。
std()和var(): 这些是标准统计公式的实现,涉及到均值、平方差等计算。ddof参数允许用户选择样本方差/标准差(ddof=1)或总体方差/标准差(ddof=0)。
diff()和pct_change(): 这些函数通过比较当前行/列与滞后periods的行/列来实现。它们在处理时间序列数据时非常有用,可以快速计算增长率、波动性等。
value_counts(): 检查分类变量的分布、识别数据不平衡、发现数据输入错误(例如,拼写错误)。
unique(): 快速查看分类变量的所有可能类别。
累积函数: 计算总销售额的增长趋势、累计投资回报。
diff() 和 pct_change(): 分析股票价格的日涨跌幅、传感器读数的瞬时变化率。
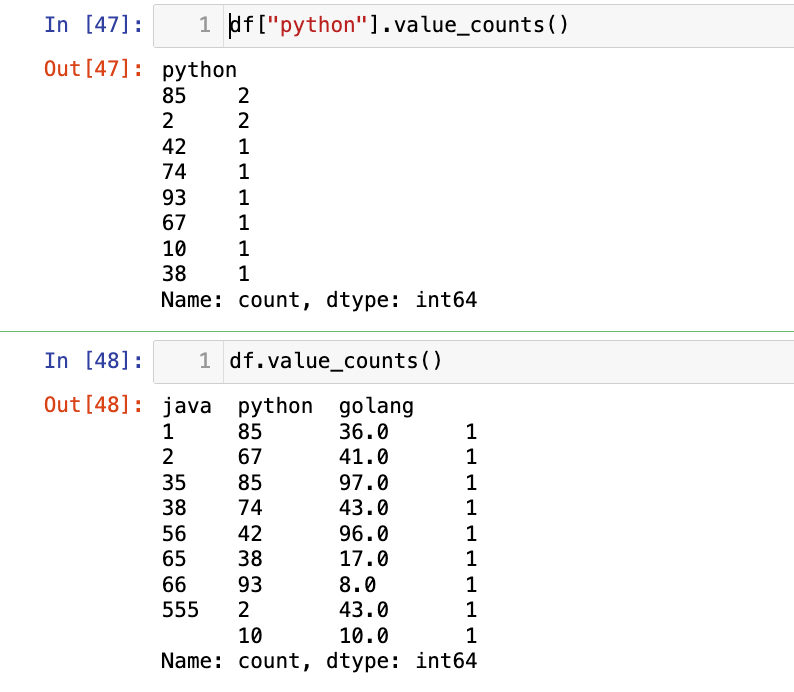
【1】统计某一列/整个df元素出现次数:
1
df["python"].value_counts()
【2】去重:
1
2
# df.unique() # AttributeError: 'DataFrame' object has no attribute 'unique'
df["java"].unique()

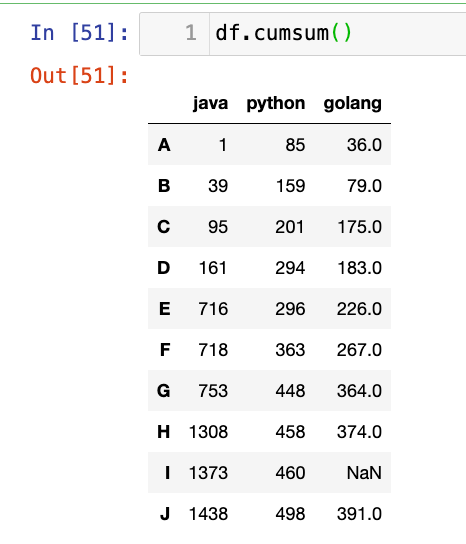
【3】累加:
1
df.cumsum()
【4】累乘:
1
df.cumprod()
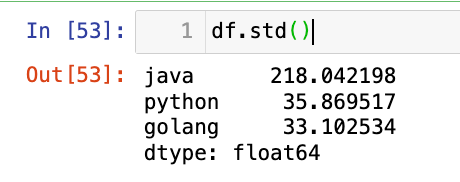
【5】标准差:
1
df.std()
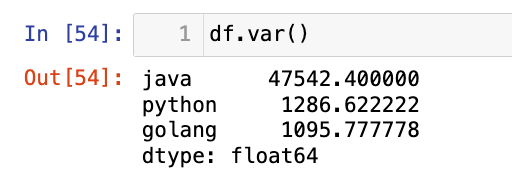
【6】方差:
1
df.var()
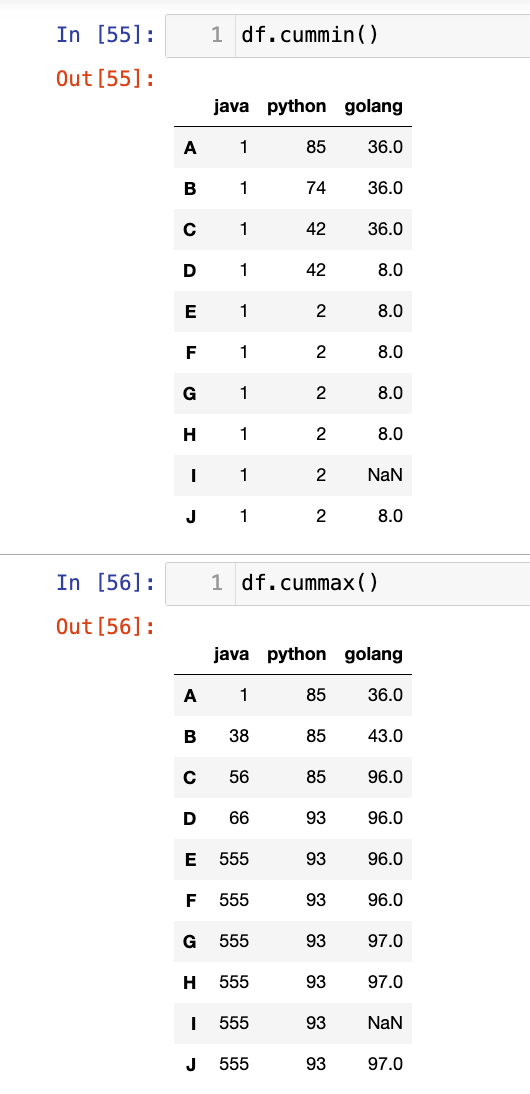
【7】累计最小值/累计最大值:
1
2
df.cummin()
df.cummax()
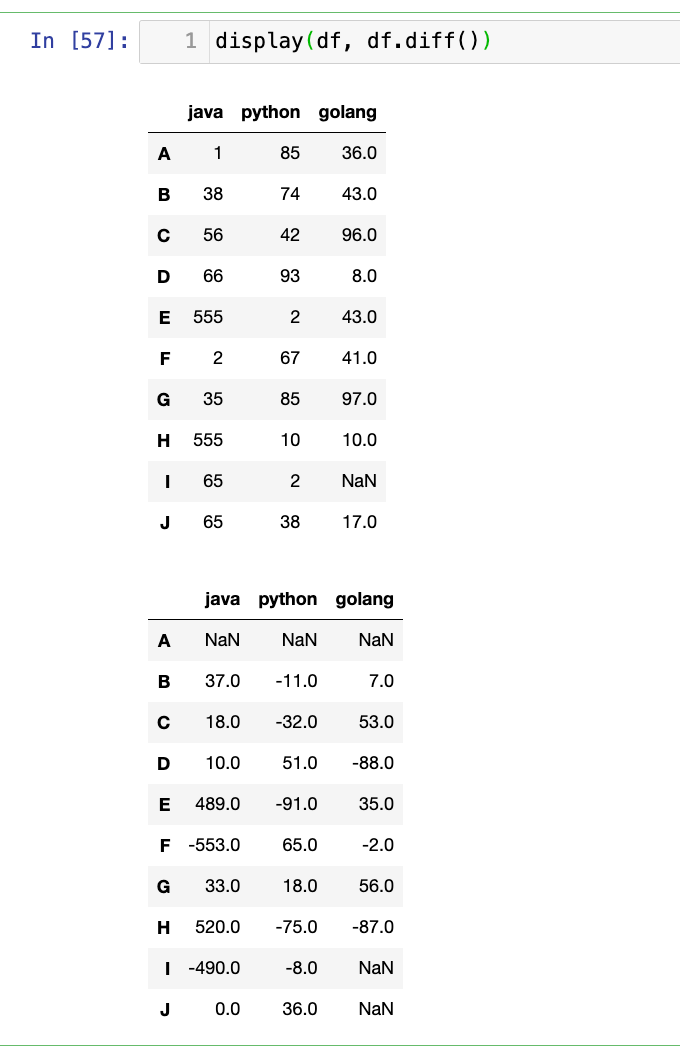
【8】差分:(当前值-前一个值)
1
display(df, df.diff())
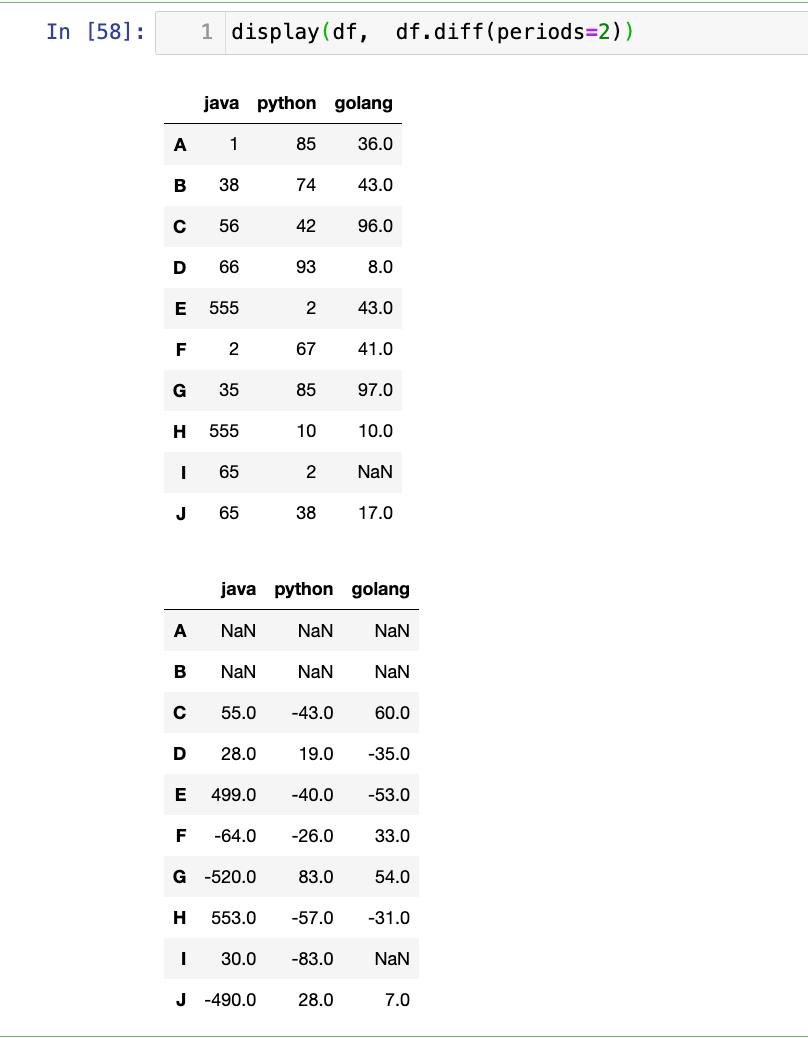
计算滞后2期的差分:
1
display(df, df.diff(periods=2))
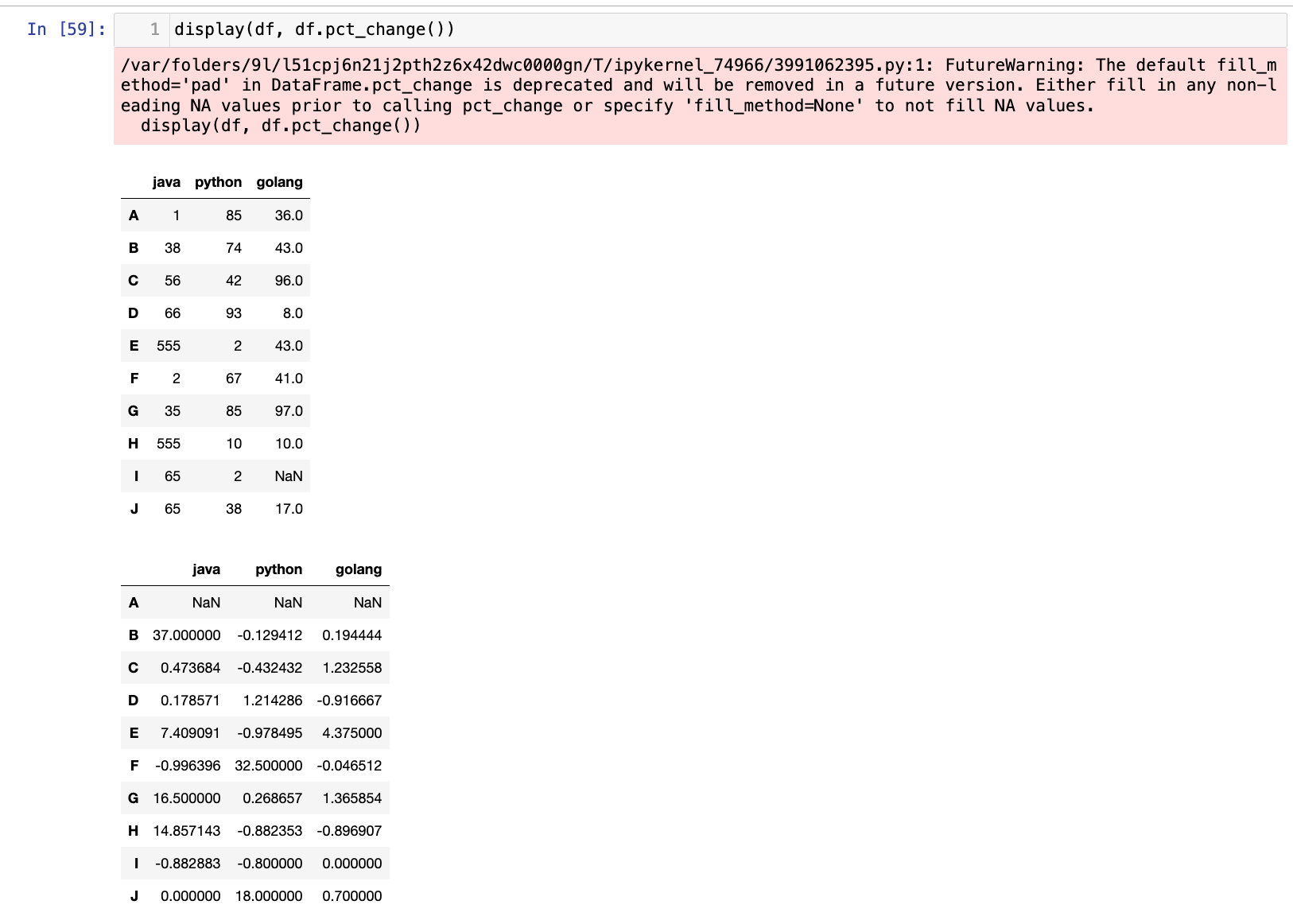
【9】计算百分比变化:((当前值-前一个值)/ 前一个值)
1
display(df, df.pct_change())
选择题
-
给定
s = pd.Series([10, 20, 10, 30, 20]),执行s.value_counts()的结果是什么?A.
Series([10, 20, 30], index=[2, 2, 1])B.
Series([10, 20, 30], index=[10, 20, 30])C.
Series([2, 2, 1], index=[10, 20, 30])D.
Series([2, 2, 1], index=[20, 10, 30])答案:C
-
以下哪个函数用于计算 Series 中所有唯一值的 NumPy 数组?
A.
s.value_counts()B.s.unique()C.s.nunique()D.s.drop_duplicates()答案:B
编程题
- 创建一个 DataFrame
stock_prices,包含'Date'(日期) 和'Price'(价格) 两列,其中'Date'是按顺序排列的日期(例如,pd.date_range),'Price'填充随机浮点数。 - 计算
'Price'列的每日价格变化(diff)。 - 计算
'Price'列的每日百分比变化(pct_change)。 - 计算
'Price'列的累积最大值和累积最小值。 - 假设
'Price'列中有一些重复的价格。统计每个价格出现的次数。 - 打印每一步操作后的结果。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# 准备 data
dates = pd.date_range(start='2025-07-01', periods=10, freq='D')
prices = [150.5, 160.2, 150.5, 170.1, 165.3, 180.7, 150.5, 175.4, 160.2, 190.8] # 包含重复价格
data = {'Date': dates, 'Price': prices}
# 创建df
stock_prices = pd.DataFrame(data=data)
display(stock_prices)
# 计算 'Price' 列的每日价格变化(diff)。
diff_ = stock_prices["Price"].diff()
display(diff_)
# 计算 'Price' 列的每日百分比变化(pct_change)
pct = stock_prices["Price"].pct_change()
display(pct)
# 计算 'Price' 列的累积最大值和累积最小值。
cummax_ = stock_prices["Price"].cummax()
cummin_ = stock_prices["Price"].cummin()
display(cummax_, cummin_)
# 假设 'Price' 列中有一些重复的价格。统计每个价格出现的次数
uni = stock_prices["Price"].unique()
counts = stock_prices["Price"].value_counts()
display(uni, counts)
4.高级统计指标
协方差和相关性是衡量两个变量之间线性关系的重要统计指标。
协方差:协方差表示的是两个变量的总体的误差,这与只表示一个变量误差的方差不同。 如果两个变量的变化趋势一致,也就是说如果其中一个大于自身的期望值,另外一个也大于自身的期望值,那么两个变量之间的协方差就是正值。 如果两个变量的变化趋势相反,即其中一个大于自身的期望值,另外一个却小于自身的期望值,那么两个变量之间的协方差就是负值。
协方差只能研究两组数据之间的关系,当要研究多组数据之间的关系时就要用到协方差矩阵。
df.cov(min_periods=None, ddof=1):- 计算 DataFrame 中所有属性(列)之间的协方差矩阵。
- 协方差矩阵是一个对称矩阵,对角线元素是每个属性的方差,非对角线元素是每对属性之间的协方差。
min_periods: 整数,计算协方差所需的最小非NA观测数。ddof: 自由度,默认为1。
Series.cov(other, min_periods=None, ddof=1):- 计算 Series 与另一个 Series 或 DataFrame 列之间的协方差。
相关系数:相关系数是最早由统计学家卡尔·皮尔逊设计的统计指标,是研究变量之间线性相关程度的量,一般用字母 r 表示。由于研究对象的不同,相关系数有多种定义方式,较为常用的是皮尔逊相关系数。
相关系数是用以反映变量之间相关关系密切程度的统计指标。相关系数是按积差方法计算,同样以两变量与各自平均值的离差为基础,通过两个离差相乘来反映两变量之间相关程度;着重研究线性的单相关系数。
皮尔逊相关系数的值在
[-1,1]之间,大于零是正相关,小于零则表示负相关,其值越接近于1或-1则表示关系越紧密,越接近于零则表示其相关性越小。
相关系数其实是在协方差的基础上进行计算的。
df.corr(method='pearson', min_periods=None):- 计算 DataFrame 中所有属性(列)之间的相关性系数矩阵。
- 相关性系数矩阵也是一个对称矩阵,对角线元素为 1,非对角线元素是每对属性之间的相关性系数。
- 相关性系数公式: 皮尔逊相关系数 r(X,Y)=fractextCov(X,Y)sqrttextVar(X)textVar(Y)。取值范围在 [−1,1] 之间。
method: 指定计算方法,默认为'pearson'(皮尔逊相关系数)。其他选项包括'kendall'(肯德尔秩相关)和'spearman'(斯皮尔曼秩相关)。
df.corrwith(other, axis=0, drop=False, method='pearson', numeric_only=False):- 计算 DataFrame 中每一列与另一个 Series 或 DataFrame 中每一列之间的相关性系数。
- 返回一个 Series,其索引是原始 DataFrame 的列名,值是与
other对应的相关系数。
pandas在底层调用高度优化的NumPy函数,这些函数又依赖于 BLAS/LAPACK 等线性代数库,从而确保了协方差和相关性矩阵计算的高性能。
特征选择: 在机器学习中,高相关性的特征可能存在冗余。可以考虑移除其中一个,以减少模型复杂性、避免多重共线性。
理解数据关系: 帮助数据科学家理解数据集中不同特征之间的相互依赖关系。
主成分分析 (PCA): PCA 的核心就是通过分析协方差矩阵(或相关系数矩阵)来找到数据的主要变化方向。
异常检测: 某些异常值可能会显著影响协方差和相关性,需要谨慎处理。
【1】协方差矩阵:
1
2
3
4
5
6
data = np.random.randint(0, 100, (10, 3))
df = pd.DataFrame(data=data, index=list("ABCDEFGHIJ"), columns=["python", "java", "golang"])
df.iloc[5, 0] = None
df.iloc[8, 2] = None
display(df)
df.cov()

计算2列的协方差:
1
df["python"].cov(df["java"])

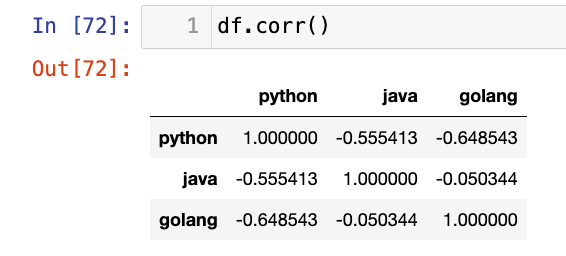
【2】相关系数矩阵:
1
df.corr()
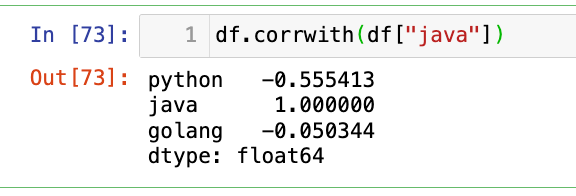
单一属性和所有其他属性的相关性系数:
1
df.corrwith(df["java"])
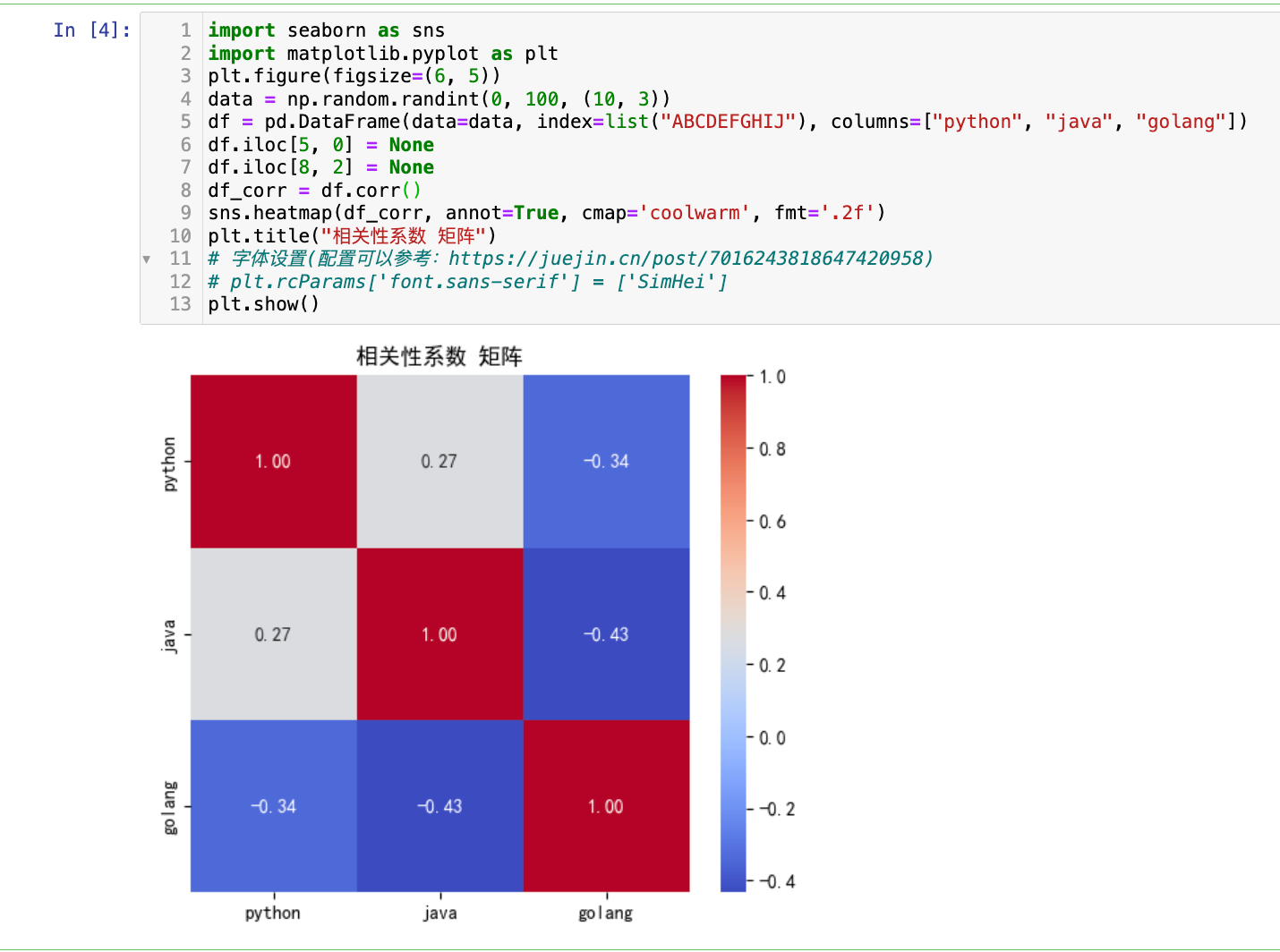
【3】可视化相关性矩阵(通常是热力图)
1
2
3
4
5
6
7
8
9
10
11
12
13
import seaborn as sns
import matplotlib.pyplot as plt
plt.figure(figsize=(6, 5))
data = np.random.randint(0, 100, (10, 3))
df = pd.DataFrame(data=data, index=list("ABCDEFGHIJ"), columns=["python", "java", "golang"])
df.iloc[5, 0] = None
df.iloc[8, 2] = None
df_corr = df.corr()
sns.heatmap(df_corr, annot=True, cmap='coolwarm', fmt='.2f')
plt.title("相关性系数 矩阵")
# 字体设置(配置可以参考:https://juejin.cn/post/7016243818647420958)
# plt.rcParams['font.sans-serif'] = ['SimHei']
plt.show()
选择题
-
以下哪个函数用于计算 DataFrame 中所有属性之间的相关性系数矩阵?
A.
df.cov()B.df.corr()C.df.corrwith()D.df.dot()答案:B,C选项用于计算 DataFrame 与另一个 Series 或 DataFrame 的列间相关系数
-
如果两个变量的皮尔逊相关系数为 −0.9,这意味着什么?
A. 它们之间没有线性关系。
B. 它们之间存在非常强的正线性关系。
C. 它们之间存在非常强的负线性关系。
D. 它们之间存在非线性关系。
答案:C
编程题
- 创建一个 DataFrame
student_performance,包含'Math_Score','Physics_Score','Chemistry_Score'三列,填充随机整数分数。 - 计算并打印所有科目之间的协方差矩阵。
- 计算并打印所有科目之间的相关性系数矩阵。
- 计算
'Math_Score'与'Physics_Score'之间的协方差。 - 计算
'Chemistry_Score'与所有其他科目之间的相关性系数。 - 解释协方差和相关性系数矩阵的结果。
1
2
3
4
5
6
7
8
9
10
11
12
13
data = np.random.randint(0, 101, (10, 3))
student_performance = pd.DataFrame(data=data, columns=["Math_Score", "Physics_Score", "Chemistry_Score"])
display(student_performance)
# 计算并打印所有科目之间的协方差矩阵
cov_matrix = student_performance.cov()
display(cov_matrix)
# 计算并打印所有科目之间的相关性系数矩阵
corr_matrix = student_performance.corr()
display(corr_matrix)
# 计算 'Math_Score' 与 'Physics_Score' 之间的协方差
display(student_performance["Math_Score"].cov(student_performance["Physics_Score"]))
# 计算 'Chemistry_Score' 与所有其他科目之间的相关性系数
display(student_performance.corrwith(student_performance["Chemistry_Score"]))