1、给定一个4维矩阵,如何得到最后两维的和?(提示,指定axis进行计算)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
X = np.random.randint(0, 10, (2, 2, 3, 3))
display(X)
"""
array([[[[9, 2, 6],
[3, 4, 9],
[7, 4, 4]],
[[1, 6, 4],
[3, 2, 7],
[6, 9, 7]]],
[[[0, 3, 4],
[2, 1, 6],
[9, 3, 8]],
[[5, 4, 1],
[7, 5, 6],
[9, 7, 9]]]])
"""
sum_last_2_d = np.sum(X, axis = (-1, -2))
sum_last_2_d
"""
array([[48, 45],
[36, 53]])
"""
2、给定数组[1, 2, 3, 4, 5],如何得到在这个数组的每个元素之间插入3个0后的新数组?
1
2
3
4
5
6
7
arr = np.arange(1, 6)
zero = np.zeros((20,),dtype=int)
zero[0::4] = arr
display(zero)
"""
array([1, 0, 0, 0, 2, 0, 0, 0, 3, 0, 0, 0, 4, 0, 0, 0, 5, 0, 0, 0])
"""
3、给定一个二维矩阵(5行4列),如何交换其中两行的元素(提示:任意调整,花式索引)?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
A = np.random.randint(0, 10, (5, 4))
display(A)
"""
array([[2, 2, 0, 0],
[1, 6, 4, 6],
[0, 3, 0, 2],
[1, 3, 8, 1],
[8, 0, 9, 0]])
"""
# 交换第一行和第2行
A[[1, 0, 2, 3, 4]]
"""
array([[1, 6, 4, 6],
[2, 2, 0, 0],
[0, 3, 0, 2],
[1, 3, 8, 1],
[8, 0, 9, 0]])
"""
如果要交换2列呢?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
display(A)
"""
array([[2, 2, 0, 0],
[1, 6, 4, 6],
[0, 3, 0, 2],
[1, 3, 8, 1],
[8, 0, 9, 0]])
"""
# 也可以用 花式索引 完成
A[:, [0, 1]] = A[:, [1, 0]]
A
"""
array([[2, 2, 0, 0],
[6, 1, 4, 6],
[3, 0, 0, 2],
[3, 1, 8, 1],
[0, 8, 9, 0]])
"""
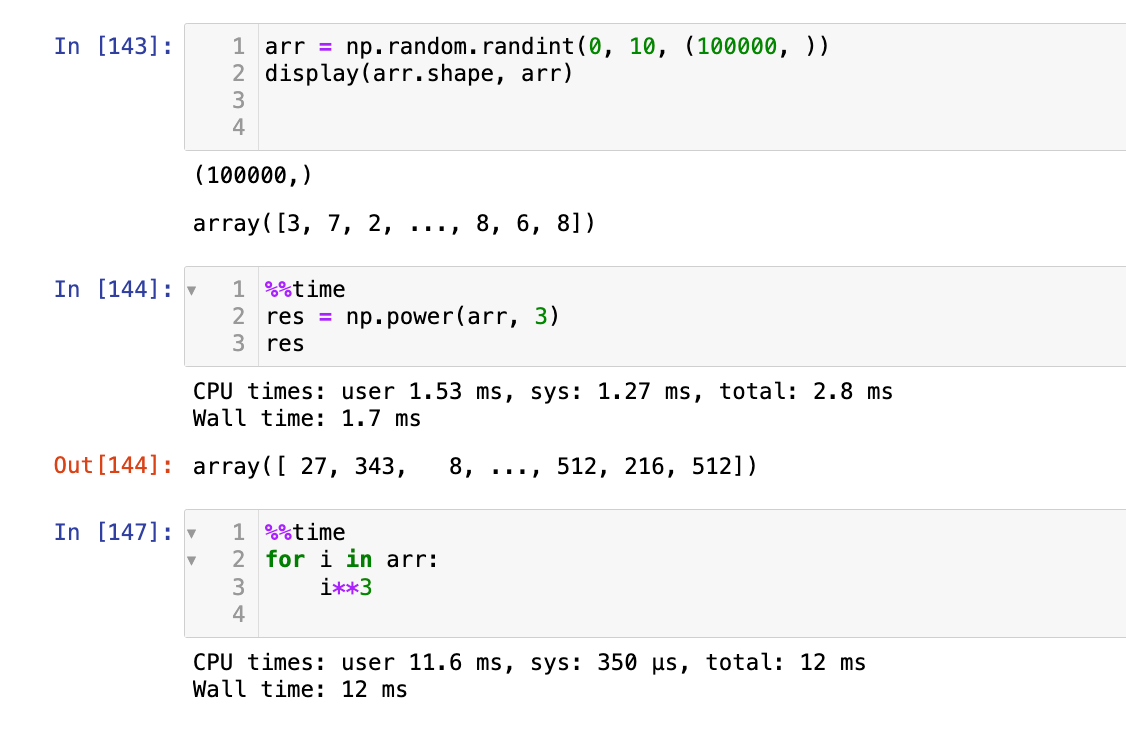
4、创建一个100000长度的随机数组,使用两种方法对其求三次方(1、for循环;2、NumPy自带方法),并比较所用时间
1
2
3
4
5
6
7
8
9
10
11
arr = np.random.randint(0, 10, (100000, ))
display(arr.shape, arr)
%%time
res = np.power(arr, 3)
res
%%time
for i in arr:
i**3
5、创建一个5行3列随机矩阵和一个3行2列随机矩阵,求矩阵积
1
2
3
4
5
6
7
8
9
10
11
X = np.random.randint(0, 10, (5, 3))
Y = np.random.randint(0, 10, (3, 2))
# 方法1:
X@Y
# 方法2:
X.dot(Y)
# 方法3:
np.dot(X, Y)
# 方法4:
np.matmul(X, Y)
6、矩阵的每一行的元素都减去该行的平均值(注意,平均值计算时指定axis,以及减法操作时形状改变)
其实不需要考虑形状改变。
1
2
3
4
X = np.random.randint(0, 10, (3, 3))
display(X)
X = X - np.mean(X, axis = 1)
display(X)
运行结果:
1
2
3
4
5
6
array([[6, 1, 9],
[8, 8, 7],
[9, 5, 3]])
array([[ 0.66666667, -6.66666667, 3.33333333],
[ 2.66666667, 0.33333333, 1.33333333],
[ 3.66666667, -2.66666667, -2.66666667]])
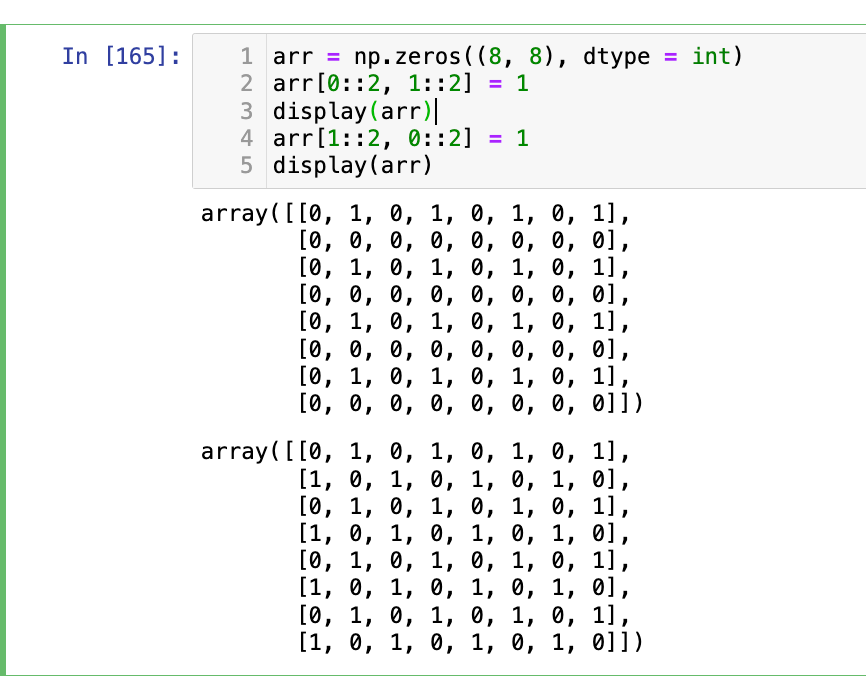
7、打印出以下函数(要求使用np.zeros创建8*8的矩阵):
1
2
3
4
5
6
7
8
9
10
[
[0 1 0 1 0 1 0 1]
[1 0 1 0 1 0 1 0]
[0 1 0 1 0 1 0 1]
[1 0 1 0 1 0 1 0]
[0 1 0 1 0 1 0 1]
[1 0 1 0 1 0 1 0]
[0 1 0 1 0 1 0 1]
[1 0 1 0 1 0 1 0]
]
1
2
3
4
5
arr = np.zeros((8, 8), dtype = int)
arr[0::2, 1::2] = 1
display(arr)
arr[1::2, 0::2] = 1
display(arr)
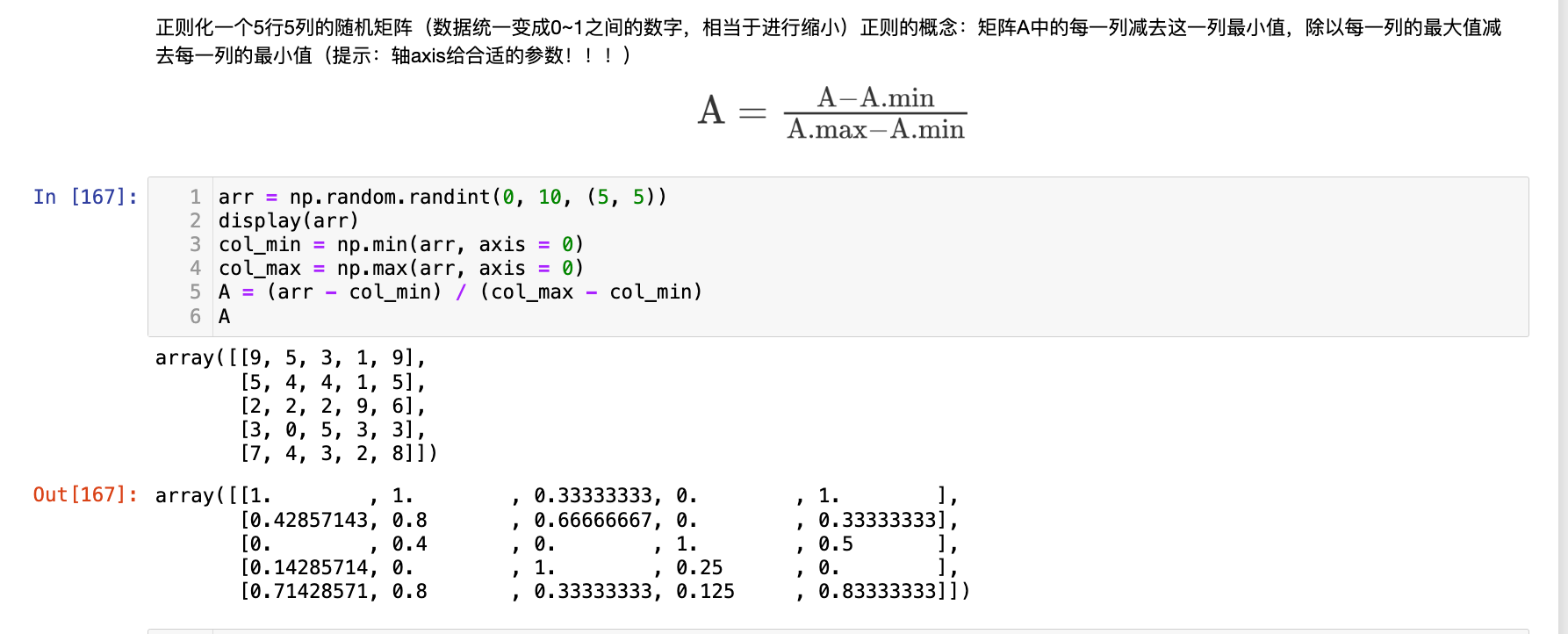
8、正则化一个5行5列的随机矩阵(数据统一变成0~1之间的数字,相当于进行缩小)
正则的概念:矩阵A中的每一列减去这一列最小值,除以每一列的最大值减去每一列的最小值(提示:轴axis给合适的参数!!!)
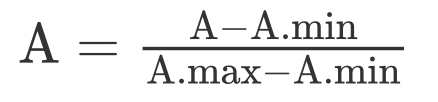
1
2
3
4
5
6
arr = np.random.randint(0, 10, (5, 5))
display(arr)
col_min = np.min(arr, axis = 0)
col_max = np.max(arr, axis = 0)
A = (arr - col_min) / (col_max - col_min)
A
9、如何根据两个或多个条件过滤numpy数组。加载鸢尾花数据,根据第一列小于5.0并且第三列大于1.5作为条件,进行数据筛选。(提示,需要使用逻辑与运算:&)
1
2
3
4
5
# 加载数据
data = np.loadtxt("./iris.csv", delimiter=",")
data_ = (data[:, 0] < 5.0) & (data[:, 2] > 1.5)
data_ = data[data_]
data_

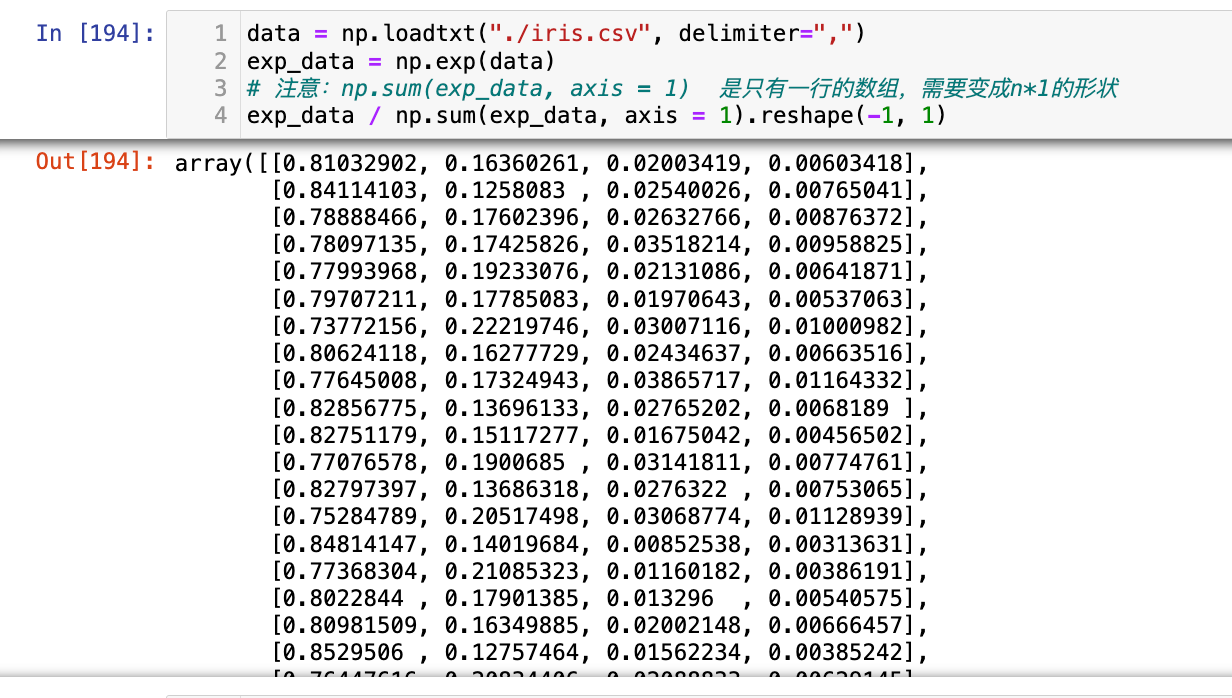
10、计算鸢尾花数据每一行的softmax得分(exp表示自然底数e的幂运算)

首先如果不理解这幅图,可以先看下面代码及其输出:

1
2
3
(np.exp(2) / (np.exp(2) + np.exp(1) + np.exp(0.1))).round(1)
(np.exp(1) / (np.exp(2) + np.exp(1) + np.exp(0.1))).round(1)
(np.exp(0.1) / (np.exp(2) + np.exp(1) + np.exp(0.1))).round(1)
所以可以这么完成这道题:
1
2
3
4
data = np.loadtxt("./iris.csv", delimiter=",")
exp_data = np.exp(data)
# 注意:np.sum(exp_data, axis = 1) 是只有一行的数组,需要变成n*1的形状
exp_data / np.sum(exp_data, axis = 1).reshape(-1, 1)