NumPy 不仅仅是一个高效的数组库，它还提供了强大的线性代数功能，这是机器学习、科学计算和数据分析的基石。

线性代数是数学的一个分支，研究向量空间和线性变换。在 NumPy 中，线性代数操作是高度优化的，通常通过 numpy.linalg 模块提供。

1.矩阵乘积

矩阵乘法是线性代数中最基本也是最重要的操作之一。它不同于逐元素乘法（Hadamard 乘积）。

定义： 只有当第一个矩阵的列数等于第二个矩阵的行数时，两个矩阵才能相乘。
- 如果矩阵 A 的形状是 (m,n)，矩阵 B 的形状是 (n,p)，那么它们的乘积 C=A * B 的形状将是 (m,p)。
计算方式： 结果矩阵 C 中的每个元素 \(C_{ij}\) 是矩阵 A 的第 i 行与矩阵 B 的第 j 列的对应元素乘积之和。

\[C_{ij}=\sum_{k=1}^nA_{ik}B_{kj}\]

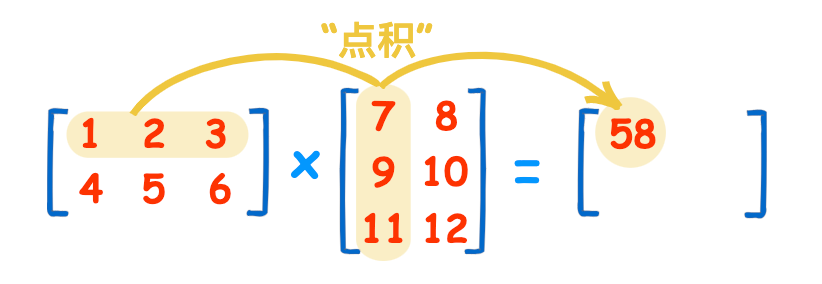
非交换性： 矩阵乘法通常不满足交换律，即 \(A*B\neq B*A\)。即使两者都可计算，结果也可能不同。
应用：
- 线性变换： 矩阵乘法可以表示空间中的旋转、缩放、剪切等线性变换。
- 线性方程组： 矩阵乘法是表示和求解线性方程组 Ax=b 的基础。
- 机器学习： 在神经网络、特征工程、主成分分析 (PCA) 等领域中广泛使用。例如，神经网络中的层就是通过矩阵乘法实现的。

NumPy 在底层使用高度优化的 BLAS (Basic Linear Algebra Subprograms) 和 LAPACK (Linear Algebra Package) 库来实现矩阵乘法。这些库通常是用 Fortran 或 C 语言编写的，并针对高性能计算进行了优化，能够充分利用多核 CPU 和 SIMD (Single Instruction, Multiple Data) 指令集。

np.dot(A, B) 函数： 这是一个通用的点积函数。

如果 A 和 B 都是一维数组，它计算向量内积（标量）。

如果 A 是二维数组，B 是一维数组，它计算矩阵与向量的乘积。

如果 A 和 B 都是二维数组（矩阵），它计算矩阵乘积。

对于更高维数组，它执行更复杂的点积运算。

@ 运算符 (Python 3.5+)： 这是 Python 专门为矩阵乘法引入的运算符，其行为与 np.matmul() 相同。它更直观地表示矩阵乘法，并且在处理多维数组时有特定的广播规则。

np.matmul(A, B)：专门用于矩阵乘法。它对二维数组的行为与 np.dot 相同，但在处理更高维数组时，其广播规则更符合矩阵乘法的语义（例如，它会将最后两个维度视为矩阵进行乘法）。

(1)矩阵乘矩阵

ma1 = np.array([[4, 2, 3], [1, 3, 1]]) # 2*3
ma2 = np.array([[2, 7], [-5, -7], [9, 3]]) # 3*2
# 方法1:
ma1@ma2
"""
array([[ 25,  23],
       [ -4, -11]])
"""
# 方法2:
np.dot(ma1, ma2)
"""
array([[ 25,  23],
       [ -4, -11]])
"""
# 方法3:
np.matmul(ma1, ma2)
"""
array([[ 25,  23],
       [ -4, -11]])
"""

(2)矩阵乘向量

ma1 = np.array([[1, 2], [3, 4]]) # 2*2
vector1 = np.array([5, 6]) # (2,)
ma1@vector1
"""
array([17, 39])# 结果是向量
"""

(3)向量内积（点积）

vec1 = np.array([1, 2, 3])
vec2 = np.array([4, 5, 6])
vec1 @ vec2   # 32

(4)选择题

给定矩阵 M = np.array([[1, 2], [3, 4]]) 和向量 v = np.array([5, 6])，以下哪个表达式可以正确计算矩阵 M 和向量 v 的乘积？

A. M * v B. np.dot(M, v) C. M @ v D. B 和 C 都是正确的。

答案：D
如果矩阵 P 的形状是 (5,3)，矩阵 Q 的形状是 (3,4)，那么矩阵乘积 P*Q 的形状是什么？ A. (5,4) B. (3,3) C. (4,5) D. 无法计算

答案：A

(5)编程题

创建两个矩阵：
- X 形状为 (4,2)，元素为 1 到 8 的整数。
- Y 形状为 (2,3)，元素为 9 到 14 的整数。
计算矩阵乘积 X*Y，并打印结果矩阵及其形状。
创建一个 3*3 的单位矩阵 I (使用 np.eye(3))。
创建一个 3*1 的列向量\(v=[1,2,3]^T\)。
计算 I*V，并打印结果。解释为什么结果是 v 本身。

X = np.arange(1, 9).reshape(4, 2)
Y = np.arange(9, 15).reshape(2, 3)
Z = X@Y
print(Z, Z.shape)
"""
[[ 33  36  39]
 [ 75  82  89]
 [117 128 139]
 [159 174 189]] (4, 3)
"""
I = np.eye(3)
V = np.array([1, 2, 3])
res = I@V
print(res)
"""
[1. 2. 3.]
"""
# 任何矩阵或者向量和单位矩阵的乘积都是其本身

2.矩阵其他计算

NumPy 的 numpy.linalg 模块提供了许多高级线性代数函数。

逆矩阵 (numpy.linalg.inv)：

定义： 对于一个方阵 A，A 的逆矩阵记作 \(A^{−1}\)，满足 \(AA^{−1}=A^{−1}A=I\)，其中 I 是单位矩阵。
条件： 只有方阵（行数等于列数）且非奇异（行列式不为零）的矩阵才存在逆矩阵。
应用： 求解线性方程组 \(Ax=b \implies x=A^{−1}b\)；在最小二乘法、卡尔曼滤波等算法中。

行列式 (numpy.linalg.det)：

定义： 行列式是一个标量值，可以从方阵的元素中计算得出。
几何意义： 在几何上，行列式的绝对值表示矩阵所代表的线性变换对空间体积的缩放因子。如果行列式为负，表示变换涉及翻转（例如，镜像）。
奇异性判断： 如果一个矩阵的行列式为零，则该矩阵是奇异矩阵（不可逆）。
应用： 判断矩阵是否可逆；计算特征值；在几何变换中。

特征值和特征向量 (numpy.linalg.eig)：

定义： 对于一个方阵 A，如果存在一个非零向量 v 和一个标量 \(\lambda\)，使得 \(Av=\lambda v\)，那么 \(\lambda\) 称为矩阵 A 的特征值，而 v 称为对应于特征值 lambda 的特征向量。
意义： 特征向量表示在矩阵变换下方向不变的向量（只被缩放），特征值表示对应的缩放因子。
应用：
- 主成分分析 (PCA)： PCA 通过计算数据协方差矩阵的特征值和特征向量来找到数据的主要变化方向（主成分）。
- 谱分析： 在图论、信号处理、量子力学等领域。
- 稳定性分析： 在动力系统和控制理论中。

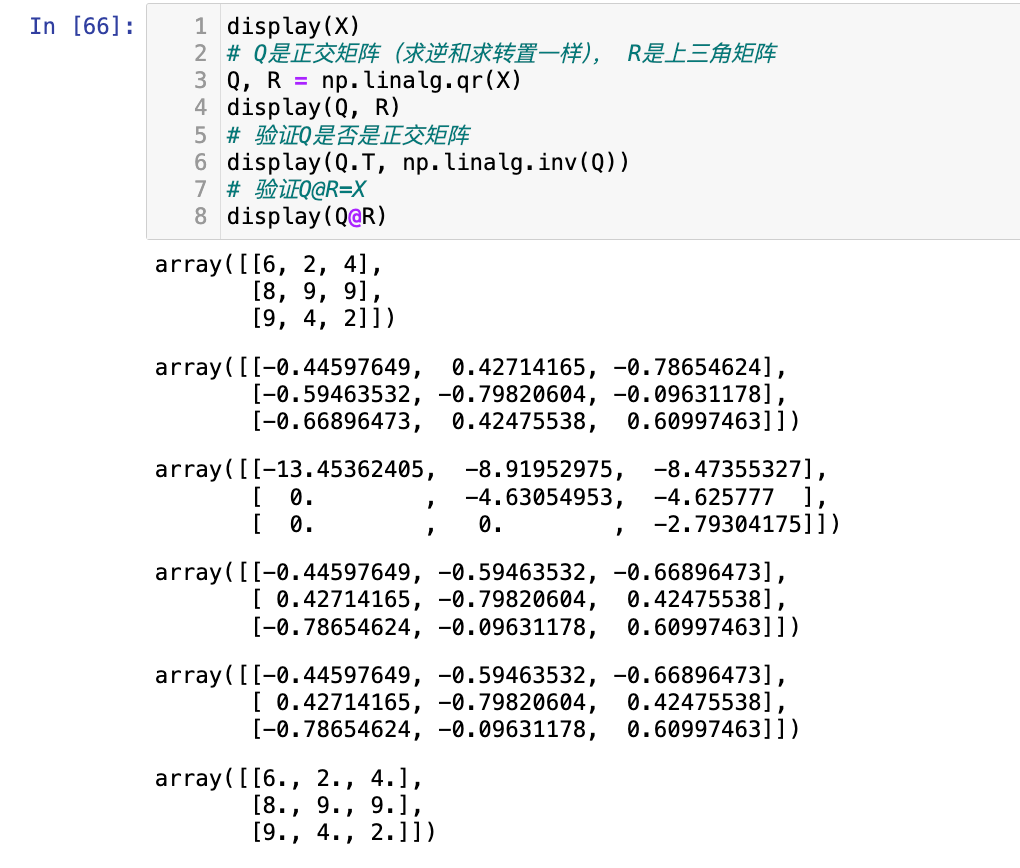
QR 分解 (numpy.linalg.qr)：

定义： 将一个矩阵 A 分解为一个正交矩阵 Q 和一个上三角矩阵 R 的乘积，即 A=QR。
- 正交矩阵 Q 满足 \(Q^TQ=I\)（即\(Q^{−1}=Q^T\)），其列向量是相互正交的单位向量。
- 上三角矩阵 R 的对角线以下元素均为零。
应用： 求解线性最小二乘问题；计算特征值；在数值稳定性要求高的场景。

奇异值分解 (SVD) (numpy.linalg.svd)：

定义： 将任意矩阵 A 分解为三个矩阵的乘积：\(A=U\Sigma V^T\)。
- U 是一个正交矩阵，其列向量是 \(AA^T\) 的特征向量。
- \(\Sigma\)是一个对角矩阵，其对角线元素是奇异值（非负），且按降序排列。
- \(V^T\) 是一个正交矩阵的转置，其行向量是 \(A^TA\) 的特征向量。
意义： SVD 揭示了矩阵最本质的结构，即使对于非方阵也适用。奇异值表示数据在各个奇异方向上的重要性。
应用：
- 降维： 通过保留最大的几个奇异值及其对应的向量来近似原始矩阵，实现数据压缩和降维（如 LSA 潜在语义分析）。
- 推荐系统： 协同过滤算法。
- 图像压缩： 通过保留少量奇异值来重建图像。
- 主成分分析 (PCA)： SVD 是 PCA 的另一种计算方法。

numpy.linalg 模块中的函数通常调用底层的 BLAS 和 LAPACK 库。这些库实现了各种数值算法来高效地计算逆、行列式、特征值/特征向量和矩阵分解。

逆矩阵计算： 通常通过高斯消元法、LU 分解等数值方法实现。

行列式计算： 可以通过 LU 分解的对角线元素的乘积来计算。

特征值/特征向量计算： 涉及到复杂的迭代算法，如 QR 算法。

QR 分解： 通常通过 Householder 变换或 Givens 旋转实现。

SVD 分解： 涉及到迭代算法，如 Golub-Kahan 算法，它本质上是对 \(A^TA\) 和 \(AA^T\) 进行特征值分解。

这些数值算法在实现时考虑了浮点数的精度问题和计算效率，以确保在实际应用中的稳定性和准确性。

【1】单位矩阵

n = 3
np.eye(n, dtype=int)
"""
array([[1, 0, 0],
       [0, 1, 0],
       [0, 0, 1]])
"""

【2】逆矩阵

单位矩阵的逆矩阵：

I = np.eye(3,dtype=int)
np.linalg.inv(I)
"""
array([[1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.]])
"""

一般方阵的逆矩阵：

# 如果希望结果展示不是科学计数法，可以这么设置
np.set_printoptions(suppress=True)
# 方阵才能求逆矩阵
X = np.random.randint(1, 10, size=(3, 3))
np.linalg.inv(X)
"""
array([[ 0.36363636,  0.27272727, -0.5       ],
       [ 1.        ,  0.        , -0.5       ],
       [-1.45454545, -0.09090909,  1.        ]])
"""

【3】行列式：

# 方阵才能求行列式，不然报错：LinAlgError: Last 2 dimensions of the array must be square
X = np.random.randint(1, 10, (3, 3))
np.linalg.det(X)
"""
-71.0
"""

【4】特征值，特征向量:

X = np.random.randint(1, 10, (3, 3))
# w:特征值，v:特征向量（列）
w, v = np.linalg.eig(X)
display(w, v)
# Av = wv  验证
print(w[0])
for i in range(len(w)):
    print(X@(v[:, i]))
    print(w[i]*(v[:, i]))

【5】奇异值分解的代码可以参考博客：程序员的数学之奇异值分解

【6】QR 分解：

display(X)
# Q是正交矩阵（求逆和求转置一样）， R是上三角矩阵
Q, R = np.linalg.qr(X)
display(Q, R)
# 验证Q是否是正交矩阵
display(Q.T, np.linalg.inv(Q))
# 验证Q@R=X
display(Q@R)

(1)选择题

如果一个方阵的行列式为零，以下哪项关于该矩阵的说法是正确的？

A. 该矩阵是单位矩阵。 B. 该矩阵是可逆的。 C. 该矩阵是奇异矩阵（不可逆）。 D. 该矩阵的特征值都为零。

答案：C，行列式为零是矩阵奇异（不可逆）的充要条件。行列式=0，推得至少有一个特征值是0，则不满秩，即矩阵奇异
在主成分分析 (PCA) 中，我们通常会计算数据协方差矩阵的什么来找到主成分？

A. 逆矩阵 B. 行列式 C. 特征值和特征向量 D. QR 分解

答案：C，PCA 的核心是通过特征值和特征向量来找到数据的主成分。

(2)编程题

创建一个 2*2 的矩阵 M = np.array([[3, 1], [2, 4]])。
计算并打印矩阵 M 的逆矩阵。
计算并打印矩阵 M 的行列式。
计算并打印矩阵 M 的特征值和特征向量。
验证其中一个特征值和特征向量是否满足 \(Mv=\lambda v\)。

M = np.array([
    [3, 1],
    [2, 4]
])
print(f"原矩阵:\n{M}")
print(f"逆矩阵:\n{np.linalg.inv(M)}")
print(f"行列式:\n{np.linalg.det(M)}")
w, v = np.linalg.eig(M)
print(f"特征值:\n{w}")
print(f"特征向量:\n{v}")
# 验证
for i in range(2):
    print(M@v[:, i])
    print(w[i]*v[:, i])

numpy-线性代数