特征值分解是一个提取矩阵特征很不错的方法,但是它只适用于方阵。而在现实的世界中,我们看到的大部分矩阵都不是方阵,比如说有 m 个学生,每个学生有 n 科成绩,这样形成的一个 m * n 的矩阵就可能不是方阵,怎样才能像描述特征值一样描述这样一般的矩阵的重要特征呢?奇异值分解就是用来干这个事的,奇异值分解是一个能适用于任意的矩阵的一种分解的方法。
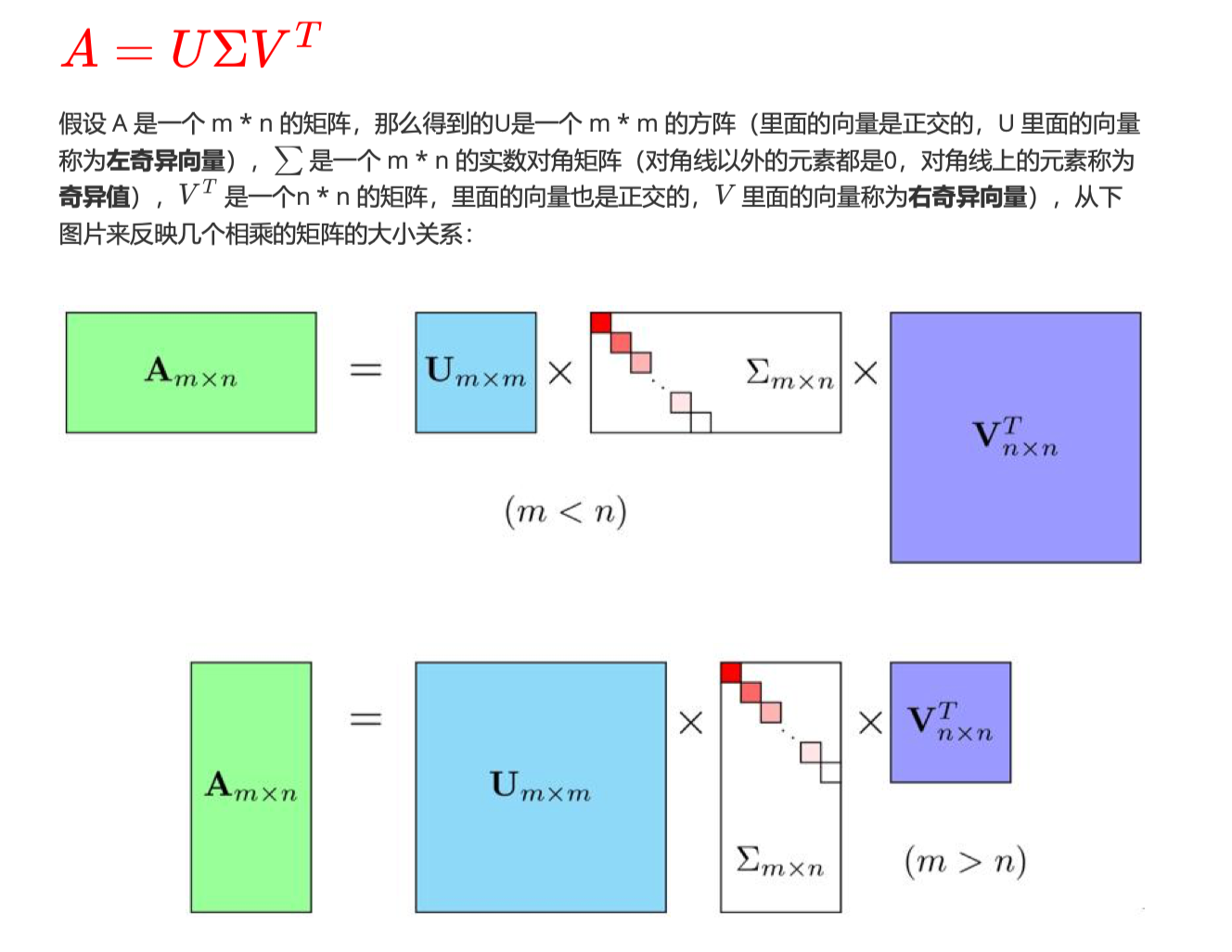
1.奇异值和特征值的关系

那么奇异值和特征值是怎么对应起来的呢?首先,我们将矩阵 A 的转置 和 A 做矩阵乘法,将会得到一个方阵,我们用这个方阵求特征值可以得到:




上面的\(\sum^{-1}\)求解也很简单,因为本身\(\sum\)是一个对角矩阵,所以求逆矩阵只需要将其对角线上的所有元素分别求倒数即可。
2.求解奇异值分解
(1)方法1:np的方法
根据NumPy提供的方法,进行奇异值求解
1
2
3
4
5
6
7
8
9
10
11
12
13
# 非方阵的矩阵
A = np.random.randint(0, 10, (5, 4))
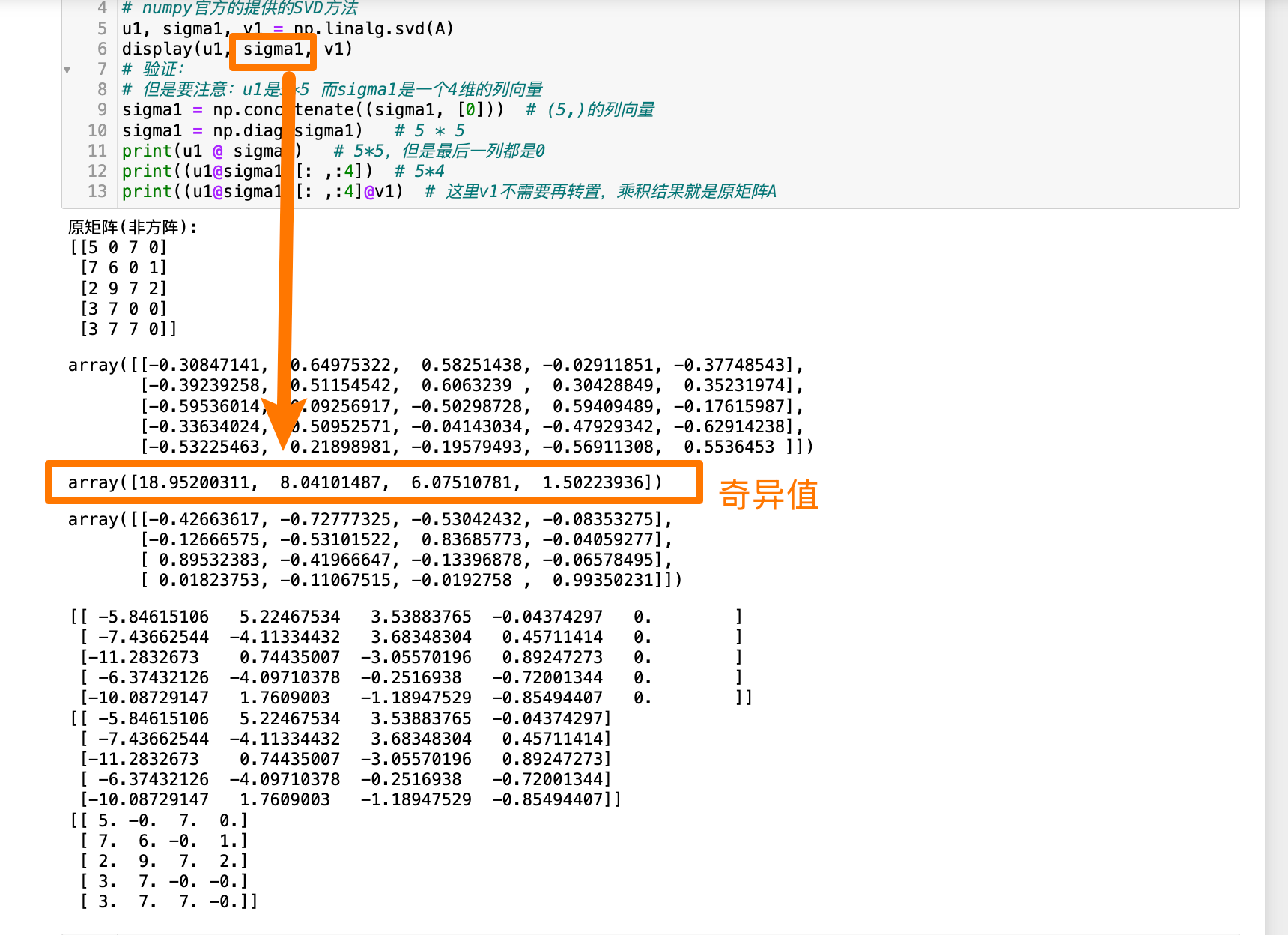
print(f"原矩阵(非方阵):\n{A}")
# numpy官方的提供的SVD方法
u1, sigma1, v1 = np.linalg.svd(A)
display(u1, sigma1, v1)
# 验证:
# 但是要注意:u1是5*5 而sigma1是一个4维的列向量
sigma1 = np.concatenate((sigma1, [0])) # (5,)的列向量
sigma1 = np.diag(sigma1) # 5 * 5
print(u1 @ sigma1) # 5*5,但是最后一列都是0
print((u1@sigma1)[: ,:4]) # 5*4
print((u1@sigma1)[: ,:4]@v1) # 这里v1不需要再转置,乘积结果就是原矩阵A

(2)自己求解奇异值分解
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# 自己实现奇异值分解
# 求左奇异矩阵U AA^T = U simgma sigma^T U^T
# simgma sigma^T需要开方
# w:奇异值的平方,v:U
w, U = np.linalg.eig(A@A.T)
# 上面中,奇异值从大到小排列,我也这样处理
arg_w = np.argsort(w)[::-1]
w = w[arg_w]
U = U[:, arg_w]
sigma = np.sqrt([s if s > 0 else 0 for s in w])
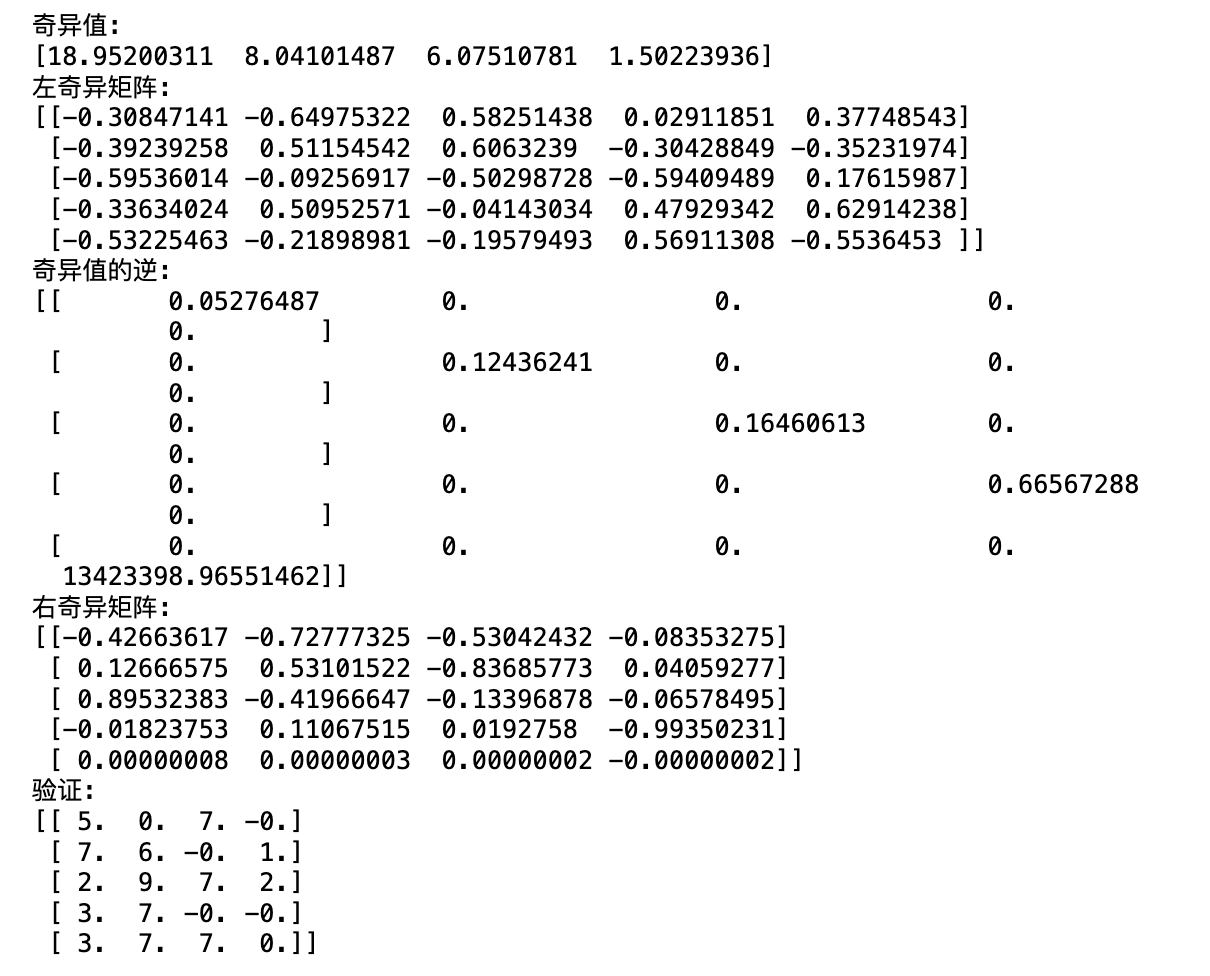
print(f"奇异值:\n{sigma[:4]}")
print(f"左奇异矩阵:\n{U}")
# 计算右奇异矩阵
# 奇异值的逆 U^T A
sigma_inv = np.diag([1/s if s > 0 else 0 for s in sigma])
print(f"奇异值的逆:\n{sigma_inv}")
V = sigma_inv@U.T@A
print(f"右奇异矩阵:\n{V}") # 5*4
# 验证
print(f"验证:\n{U@np.diag(sigma)@V}")
3.奇异值分解的性质
奇异值 \(\sigma_i\)跟特征值类似,在矩阵\(\sum\)中也是从大到小排列,而且\(\sigma\)的减小特别的快,在很多情况下,前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上了。也就是说,我们也可以用前 r 大的奇异值来近似描述矩阵,这里定义一下部分奇异值分解:

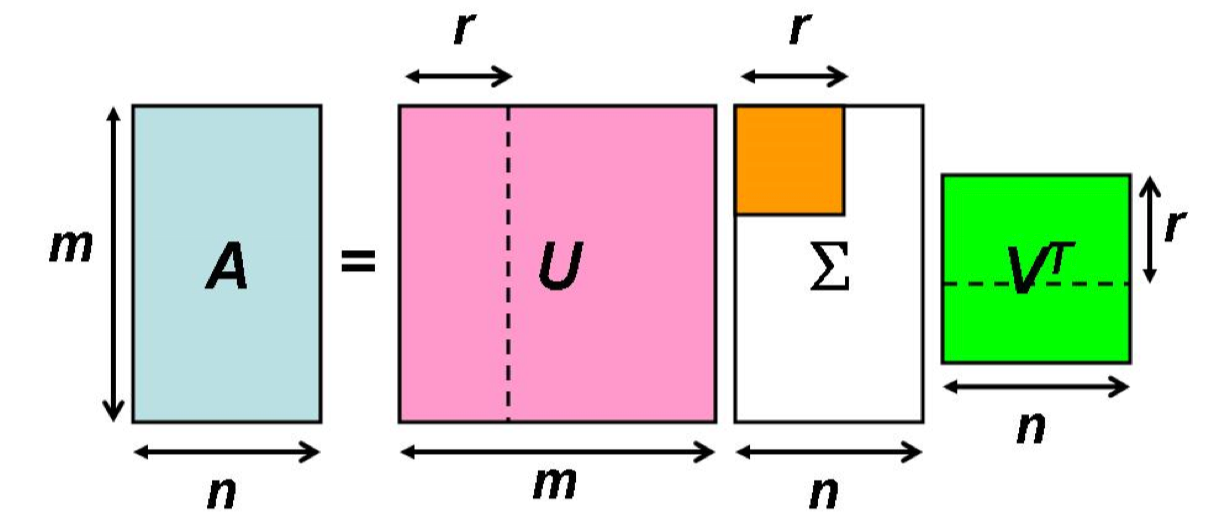
右边的三个矩阵相乘的结果将会是一个接近于 A 的矩阵,在这儿,r 越接近于 n,则相乘的结果越接近于A。
而这三个矩阵的面积之和(在存储观点来说,矩阵面积越小,存储量就越小)要远远小于原始的矩阵 A,我们如果想要压缩空间来表示原矩阵 A,我们存下这里的三个矩阵:\(U、Σ、V\)就好了。
说句大白话,称作「奇异值」可能无法顾名思义迅速理解其本质,那咱们换个说法,称作「主特征值」,你可能就迅速了然了。 对于非奇异(满秩)矩阵,对应着特征值;对于奇异矩阵,就需要进行奇异值分解,对应着奇异值。
对于奇异矩阵,将A与其转置相乘将会得到一个方阵\(AA^T\),再求特征值。值得注意的是,对于非奇异矩阵进行奇异值分解(SVD),得到的奇异值,其实就是特征值。
下面代码可以修改r的值:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import numpy as np
matrix1 = np.random.randint(1, 10, size=(5, 4)) # 5行4列的矩阵
print(f"原矩阵:\n{matrix1}")
U, sigma, V = np.linalg.svd(matrix1)
print(f"左奇异矩阵:\n{U}")
print(f"奇异值:\n{sigma}")
print(f"右奇异矩阵:\n{V}")
# 验证
sigma2matrix = np.diag(np.concatenate((sigma, [0])))
# print(sigma2matrix)
print(f"还原验证:U@sigma@V:\n{(U@sigma2matrix)[:,:4]@V}")
# 选择前r大的奇异值
r = 3
# 验证
verify_matrix = ((U[:, :r])@(sigma2matrix[:r, :r]))[:,:4]@(V[:r,:])
print(f"还原验证(只取前r大):\n{verify_matrix.round(2)}")
