NumPy 的核心优势之一在于其对“通用函数”（Universal Functions，通常简称为 UFuncs）的支持。UFuncs 是对 ndarray 对象进行逐元素操作的函数。它们是 NumPy 性能的关键，因为它们在 C 语言层面实现，并且能够自动利用矢量化和广播机制，从而在处理大型数组时提供极高的效率。

1.元素级数字函数

通用函数（UFuncs）是 NumPy 提供的一系列对数组进行逐元素操作的函数。它们可以应用于单个数组（一元 UFuncs）或两个数组（二元 UFuncs）。UFuncs 的主要特点是：

逐元素操作： 对数组中的每个元素独立地执行相同的操作。
矢量化： 无需显式循环，操作在底层 C 语言级别并行执行，效率极高。
广播支持： 如果输入数组的形状不兼容，UFuncs 会尝试应用广播机制来使它们兼容。
灵活性： 许多 UFuncs 接受可选参数，例如 out 参数用于指定结果存储的数组，where 参数用于有条件地执行操作。

常见的元素级数字 UFuncs 包括：

一元 UFuncs (对单个数组操作)：
- np.abs(x)：计算绝对值。
- np.sqrt(x)：计算平方根。
- np.square(x)：计算平方。
- np.exp(x)：计算指数 ex。
- np.log(x)：计算自然对数。
- np.sin(x), np.cos(x), np.tan(x)：计算三角函数。
- np.ceil(x)：向上取整。
- np.floor(x)：向下取整。
- np.round(x)：四舍五入。
- np.negative(x)：取负数。
- np.reciprocal(x)：计算倒数 1/x。
二元 UFuncs (对两个数组操作)：
- np.add(x, y)：加法（x + y）。
- np.subtract(x, y)：减法（x - y）。
- np.multiply(x, y)：乘法（x * y）。
- np.divide(x, y)：除法（x / y）。
- np.power(x, y)：指数运算（xy）。
- np.maximum(x, y)：逐元素返回两个数组中的较大值。
- np.minimum(x, y)：逐元素返回两个数组中的较小值。
- np.greater(x, y)：逐元素比较 x>y。
- np.less(x, y)：逐元素比较 x\<y。
- np.equal(x, y)：逐元素比较 x==y。

注意： 像 np.inner 这样的函数（用户示例中提到）不是 UFunc，它属于线性代数操作，执行的是向量内积或矩阵乘法，而不是逐元素的运算。np.all 和 np.any 属于聚合函数，将在后面的章节介绍。np.clip 是一个非 UFunc 的数组操作函数。

UFuncs 的高性能得益于其底层实现：

C 语言实现： 所有的 UFuncs 都是用高度优化的 C 语言编写的。这意味着它们绕过了 Python 解释器的开销，直接在底层执行计算。

矢量化操作： UFuncs 能够对整个数组进行操作，而不是通过 Python 循环逐个处理元素。这种矢量化是 NumPy 性能的核心。在底层，NumPy 会尽可能地利用 SIMD（Single Instruction, Multiple Data）指令集，允许 CPU 同时对多个数据点执行相同的操作。

广播机制集成： UFuncs 内置了广播机制。当您对形状不同的数组执行 UFunc 操作时，NumPy 会自动应用广播规则，逻辑上扩展较小的数组，而无需实际复制数据，从而进一步提高内存效率和计算速度。

内存连续性： NumPy 数组通常在内存中是连续存储的（C 序或 Fortran 序）。UFuncs 可以高效地遍历这些连续的内存块，最大限度地减少缓存未命中。

2.where函数

np.where() 函数是 NumPy 中一个非常强大的条件选择函数，它类似于 Python 中的三元运算符 x if condition else y 的矢量化版本。它的基本语法是 np.where(condition, x, y)，其中：

condition：一个布尔数组（或可广播到布尔数组的表达式）。
x：当 condition 为 True 时选择的值（可以是标量或数组）。
y：当 condition 为 False 时选择的值（可以是标量或数组）。

np.where() 会返回一个新数组，其形状与 condition、x 和 y 广播后的形状相同。新数组中的每个元素都根据 condition 中对应位置的布尔值来选择 x 或 y 中的元素。

拓展用法：

仅传入 condition 参数： 如果只提供 condition 参数，np.where(condition) 会返回一个元组，其中包含满足条件（True）的元素的索引。对于一维数组，它返回一个包含索引的元组；对于多维数组，它返回一个元组，每个元素都是一个数组，表示每个维度上的索引。这与 np.argwhere() 类似，但返回的格式不同。

np.where() 的高效性在于它避免了显式的 Python 循环。在底层，它执行以下操作：

布尔掩码创建： 首先，condition 被评估并转换为一个布尔数组。

逐元素选择： NumPy 内部的 C 语言代码会遍历这个布尔掩码。对于掩码中为 True 的位置，它会从 x 中获取相应的值；对于为 False 的位置，它会从 y 中获取相应的值。

广播支持： condition、x 和 y 都可以是不同形状的数组，只要它们满足 NumPy 的广播规则即可。np.where() 会在内部处理这些广播，生成一个与广播结果形状相同的新数组。

数据复制： np.where() 总是返回一个新的数组副本，因为结果数组的元素可能来自不同的输入数组，需要重新组合。

【1】基础用法：

arr1 = np.arange(1, 10, 2)
arr1
"""
array([1, 3, 5, 7, 9])
"""
arr2 = np.arange(2, 11, 2)
arr2
"""
array([ 2,  4,  6,  8, 10])
"""
cond = np.array([True, False, True, True, False])
res1 = np.where(cond, arr1, arr2)
res1
"""
array([ 1,  4,  5,  7, 10])
"""

【2】根据条件替换数组中的值

arr = np.random.randint(0, 30, size=10)
print(arr)   # [ 6 26 13  0 12  4 26  8 19  7]
# 大于15的设置成-15
res1 = np.where(arr < 15, arr, -15)
res1 
"""
array([  6, -15,  13,   0,  12,   4, -15,   8, -15,   7])
"""

【3】仅传入条件参数

arr1 = np.array([10, 20, 5, 30, 15, 25])
# 大于15的元素的索引值
arr1_bigger_15_index = np.where(arr1 > 15)
arr1_bigger_15_index   
"""
(array([1, 3, 5]),)
"""
gt_15_index = arr1_bigger_15_index[0]
gt_15_index
"""
array([1, 3, 5])
"""
# 得到实际大于15的值
arr1[gt_15_index]
"""
array([20, 30, 25])
"""

(1)选择题

给定以下代码：

import numpy as np
data = np.array([10, 5, 20, 15, 30])
result = np.where(data > 15, data * 2, data / 2)

result 数组的值是什么？ A. array([20., 10., 40., 30., 60.]) B. array([ 5., 2.5, 40., 7.5, 60.]) C. array([10., 5., 40., 15., 60.]) D. array([ 5., 2.5, 20., 7.5, 30.])

答案：B

以下关于 np.where() 的描述，哪一项是错误的？

A. 它可以根据条件从两个数组中选择元素。 B. 它总是返回一个新的数组副本。

C. 如果只提供条件参数，它会返回满足条件的元素的索引。 D. 它只能用于一维数组。

答案：D

(2)编程题

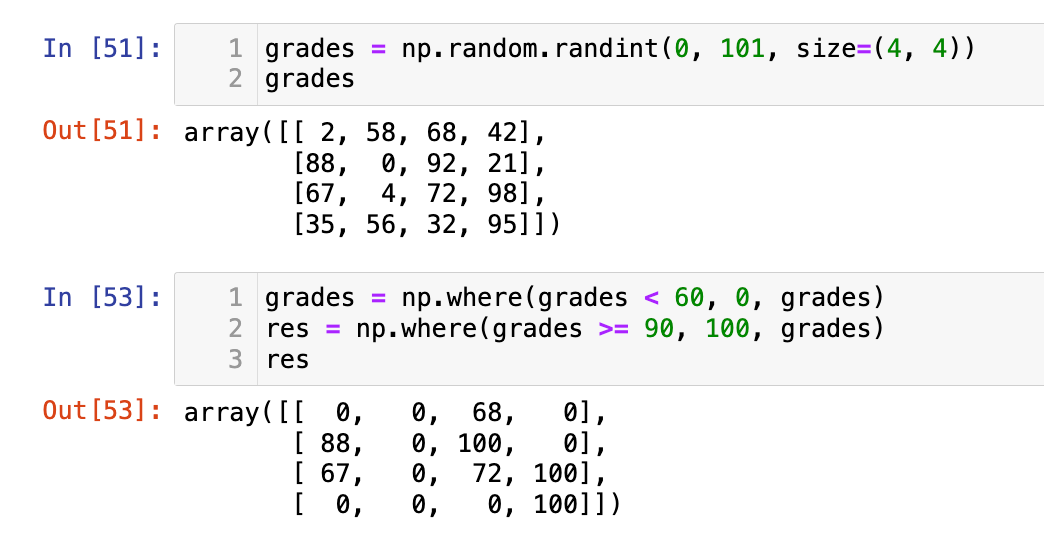
创建一个4*4 的 NumPy 数组 grades，包含 0 到 100 的随机整数，表示学生的成绩。
使用 np.where() 函数：
- 将所有小于 60 的成绩替换为 0（不及格）。
- 将所有大于等于 90 的成绩替换为 100（优秀）。
打印原始成绩数组和每次操作后的数组。

grades = np.random.randint(0, 101, size=(4, 4))
grades

grades = np.where(grades < 60, 0, grades)
res = np.where(grades >= 90, 100, grades)
res

3.排序方法

NumPy 提供了多种灵活的排序方法，可以对数组进行就地排序、返回排序后的副本或返回排序后的索引。理解这些方法的区别对于有效管理数据至关重要。

ndarray.sort(axis=-1, kind='quicksort', order=None)：就地排序
- 这是一个数组对象的方法，它会直接修改原始数组，不返回新数组。
- axis：指定沿着哪个轴进行排序。默认是 -1（最后一个轴）。如果 axis=None，则数组会被展平并排序。
- kind：排序算法，可选 'quicksort' (默认), 'mergesort', 'heapsort', 'stable'。
- order：用于结构化数组的字段名。
np.sort(a, axis=-1, kind='quicksort', order=None)：返回排序后的副本
- 这是一个 NumPy 函数，它返回一个原始数组的排序副本，而不会修改原始数组。
- 参数与 ndarray.sort() 类似。
ndarray.argsort(axis=-1, kind='quicksort', order=None)：返回排序后的索引
- 这是一个数组对象的方法，它返回一个整数数组，表示原始数组元素在排序后的位置。换句话说，它返回的是能够对原始数组进行排序的索引。
- 例如，如果 arr[i] 是最小的元素，那么 argsort() 返回的数组的第一个元素就是 i。
- 这对于间接排序非常有用，即根据一个数组的排序顺序来重新排列另一个数组。

NumPy 的排序功能在底层使用了高度优化的 C/C++ 实现，通常是混合排序算法，以在不同数据集大小和特性下提供最佳性能。

就地排序 vs. 副本：

ndarray.sort() 之所以是就地排序，是因为它直接操作了原始数组的数据缓冲区。这避免了内存分配和数据复制的开销，因此在处理大型数组时效率更高，但会改变原始数据。

np.sort() 返回副本，因为它需要分配新的内存空间来存储排序后的结果，并将原始数据复制到新空间中，然后在新空间中进行排序。这保证了原始数据的完整性。

argsort 的原理： argsort 不直接对数据进行排序，而是构建一个索引数组。这个索引数组的每个元素 j 对应原始数组中第 j 个元素在排序后数组中的位置。例如，如果 arr[k] 是排序后的第一个元素，那么 argsort() 结果的第一个元素就是 k。这允许您“间接”地排序其他相关数组，而无需重新排列它们的数据。

【1】原地排序：

arr = np.random.randint(-8, 20, size=(8,))
arr
# 原地排序
arr.sort()
arr
"""
array([-6, -4, -4, -3, 13, 14, 17, 18])
"""

【2】多维数组的原地排序：

【3】深拷贝排序：

# 深拷贝排序
arr = np.random.randint(-8, 20, size=(8,))
res_arr = np.sort(arr)
res_arr 
"""
array([-6, -5, 10, 11, 12, 15, 15, 16])
"""

arr2d = arr.reshape(4, 2)
# 按行排序
res2 = np.sort(arr2d, axis = 1)
res2
"""
array([[-7, 13],
       [-1,  8],
       [ 1, 19],
       [ 5, 17]])
"""
# 按列排序
res3 = np.sort(arr2d, axis = 0)
res3
"""
array([[-7, -6],
       [ 8, -5],
       [ 8, -2],
       [16,  3]])
"""

【4】返回排序后的索引：

arr = np.random.randint(-8, 20, size=(8,))
ind = arr.argsort()  #得到排序之后的索引
# 根据索引得到排序后的数组
arr[ind]   
"""
array([-8,  1,  5,  5, 11, 13, 14, 19])
"""

【5】间接排序：根据一个数组的顺序排序另一个数组：

names = np.array(["Alice", "Bob", "Cathy", "David"])
scores = np.array([89, 79, 90, 75])
# 分数从低到高排序：
ind = scores.argsort()
names[ind]
"""
array(['David', 'Bob', 'Alice', 'Cathy'], dtype='<U5')
"""

选择题

给定 arr = np.array([5, 1, 8, 2])，执行 arr.sort() 后，arr 的值是什么？

A. array([1, 2, 5, 8]) B. array([5, 1, 8, 2]) C. array([1, 3, 0, 2]) D. 报错

答案：A，原地操作
以下哪个函数会返回一个新数组，其中包含原始数组排序后的索引

A. np.sort() B. ndarray.sort() C. ndarray.argsort() D. np.unique()

答案：C

编程题

创建一个 3*3 的 NumPy 数组 data_matrix，包含 0 到 8 的随机整数。
对 data_matrix 进行以下操作：
- 使用 np.sort() 按行排序，并打印结果。验证原始数组未被修改。
- 使用 ndarray.sort() 按列排序，并打印结果。验证原始数组已被修改。
- 使用 ndarray.argsort() 获取按行排序的索引，并打印这些索引。
创建一个包含学生姓名和分数的两个一维数组，例如 student_names = np.array(['Alice', 'Bob', 'Charlie']) 和 student_scores = np.array([85, 92, 78])。使用 argsort 根据分数从高到低对姓名进行排序，并打印排序后的姓名。

data_matrix = np.random.randint(0, 9, size=(3, 3))   # 默认axis=0
print(np.sort(data_matrix))
"""
[[1 4 8]
 [5 5 7]
 [0 7 8]]
"""
print("原始数组：")
print(data_matrix)   # 发现  原始数组没有改变
"""
[[1 4 8]
 [5 5 7]
 [7 0 8]]
"""
# 按列排序
# 先拷贝原数组
arr_copy = data_matrix.copy()
arr_copy.sort(axis=0)
print(arr_copy)
"""
[[1 0 7]
 [5 4 8]
 [7 5 8]]
"""
# 按行排序（索引）
arr_index = data_matrix.argsort(axis=1)
print(arr_index)
"""
[[0 1 2]
 [0 1 2]
 [1 0 2]]
"""

4.集合运算函数

NumPy 提供了专门用于处理一维数组（被视为集合）的函数，它们可以执行常见的集合操作，如交集、并集、差集和唯一元素查找。这些函数通常要求输入数组是排序的，或者它们会在内部对数组进行排序以提高效率。

np.unique(ar)：查找唯一元素
- 返回输入数组中唯一元素的排序副本。
- 可选参数 return_index=True 返回唯一元素在原数组中的索引。
- 可选参数 return_inverse=True 返回原数组元素在唯一数组中的索引。
- 可选参数 return_counts=True 返回每个唯一元素的出现次数。
np.intersect1d(ar1, ar2, assume_unique=False)：计算两个数组的交集
- 返回两个数组中都存在的唯一元素的排序副本。
- assume_unique=True：如果已知输入数组是唯一的且已排序，可以设置为 True 以提高性能。
np.union1d(ar1, ar2)：计算两个数组的并集
- 返回两个数组中所有唯一元素的排序副本。
np.setdiff1d(ar1, ar2, assume_unique=False)：计算两个数组的差集
- 返回在 ar1 中存在但在 ar2 中不存在的唯一元素的排序副本。
np.setxor1d(ar1, ar2, assume_unique=False)：计算两个数组的对称差集
- 返回在 ar1 或 ar2 中存在，但不同时存在于两者中的唯一元素的排序副本。
np.in1d(ar1, ar2, assume_unique=False, invert=False)：测试数组元素是否在另一个数组中
- 返回一个布尔数组，其形状与 ar1 相同。如果 ar1 中的元素存在于 ar2 中，则对应位置为 True，否则为 False。
- invert=True 可以反转结果。

NumPy 的集合运算函数通常依赖于排序和高效的比较算法。

排序： 大多数集合操作（如交集、并集、差集）在内部会先对输入数组进行排序。这是因为对已排序的数组进行比较和合并操作要比对未排序的数组高效得多。例如，在查找交集时，可以通过两个指针同时遍历两个排序数组来快速找到共同元素。

唯一性处理： np.unique 以及其他集合函数在返回结果时，会确保结果中只包含唯一元素。这通常通过在排序后移除相邻的重复项来实现。

内存效率： 尽管这些函数会返回新的数组副本（因为结果的长度和内容通常与输入不同），但底层的 C 语言实现确保了这些操作的内存分配和数据复制是高度优化的。

(1)np.unique

arr = np.random.randint(0, 6, (9))
print(arr)
"""
[4 2 3 1 2 0 2 0 0]
"""
arr_uni = np.unique(arr)
print(arr_uni)
"""
[0 1 2 3 4]
"""

uni_ele, indices, counts = np.unique(arr, return_counts=True, return_index=True)
print(uni_ele)  # [0 1 2 3 4 5]
print(indices)  # [7 4 6 0 2 1] 第一次出现的位置
print(counts)   # [1 1 2 2 1 2]

(2)集合运算

arr1 = np.arange(2, 11, 2)
arr1  # array([ 2,  4,  6,  8, 10])
arr2 = np.arange(3, 8)
arr2  # array([3, 4, 5, 6, 7])
# 交集
intersect = np.intersect1d(arr1, arr2)
intersect   # array([4, 6])
# 并集
union_set = np.union1d(arr1, arr2)
union_set   # array([ 2,  3,  4,  5,  6,  7,  8, 10])
# 差集
diff_ = np.setdiff1d(arr1, arr2)
diff_  # array([ 2,  8, 10])
# 对称差集
xor_ = np.setxor1d(arr1, arr2)
xor_   # array([ 2,  3,  5,  7,  8, 10])
# 元素是否在另一数组中
test_ele = np.array([4, 1, 8, 5])
is_in_A = np.in1d(test_ele, arr1)
is_in_A  # array([ True, False,  True, False])

(3)选择题

给定 arr1 = np.array([1, 2, 3, 2, 1])，np.unique(arr1) 的结果是什么？

A. array([1, 2, 3, 2, 1]) B. array([1, 2, 3]) C. array([2, 1, 3]) D. array([3, 2, 1])

答案：B，np.unique() 返回唯一元素的排序副本。
以下哪个函数会返回在第一个数组中存在但在第二个数组中不存在的元素？

A. np.intersect1d() B. np.union1d() C. np.setdiff1d() D. np.setxor1d()

答案：C，np.setdiff1d(A, B) 返回在 A 中但不在 B 中的元素。（差集）

(4)编程题

创建两个 NumPy 数组：cities1 = np.array(['New York', 'London', 'Paris', 'Tokyo', 'London']) 和 cities2 = np.array(['Paris', 'Berlin', 'Rome', 'New York'])。
执行以下集合运算并打印结果：
- 找出 cities1 中的所有唯一城市。
- 找出 cities1 和 cities2 的交集。
- 找出 cities1 和 cities2 的并集。
- 找出只在 cities1 中出现而不在 cities2 中出现的城市。
- 使用 np.in1d 检查 ['London', 'Rome', 'Tokyo'] 这些城市是否在 cities2 中。

cities1 = np.array(['New York', 'London', 'Paris', 'Tokyo', 'London'])
cities2 = np.array(['Paris', 'Berlin', 'Rome', 'New York'])
res1 = np.unique(cities1)
res1  # array(['London', 'New York', 'Paris', 'Tokyo'], dtype='<U8')
res2 = np.intersect1d(cities1, cities2)
res2  # array(['New York', 'Paris'], dtype='<U8')
res3 = np.union1d(cities1, cities2)
res3  
# array(['Berlin', 'London', 'New York', 'Paris', 'Rome', 'Tokyo'], dtype='<U8')
res4 = np.setdiff1d(cities1, cities2)
res4   # array(['London', 'Tokyo'], dtype='<U8')
test_ele = np.array(['London', 'Rome', 'Tokyo'])
res5 = np.in1d(test_ele, cities2)
res5   # array([False,  True, False])

5.数学和统计函数

NumPy 提供了大量的数学和统计函数，用于计算数组的各种属性，如最小值、最大值、平均值、标准差等。这些函数通常可以应用于整个数组，也可以沿着指定的轴（维度）进行计算。

聚合函数（Aggregation Functions）： 对数组中的元素进行汇总计算。
- ndarray.min(), np.min(arr)：计算最小值。
- ndarray.max(), np.max(arr)：计算最大值。
- ndarray.sum(), np.sum(arr)：计算总和。
- ndarray.mean(), np.mean(arr)：计算算术平均值。
- ndarray.std(), np.std(arr)：计算标准差。
- ndarray.var(), np.var(arr)：计算方差。
- np.median(arr)：计算中位数（这是一个 NumPy 函数，不是 ndarray 方法）。
- axis 参数： 对于多维数组，axis 参数指定了执行操作的轴。
  - axis=0：沿着列方向操作（对每列进行聚合）。
  - axis=1：沿着行方向操作（对每行进行聚合）。
  - axis=None (默认)：对整个数组进行操作。
- keepdims=True： 保留聚合维度，使其结果形状与原始数组兼容，方便广播。
累积/累乘函数：
- np.cumsum(arr, axis=None)：计算累积和。
- np.cumprod(arr, axis=None)：计算累积乘积。
位置函数：
- ndarray.argmin(axis=None), np.argmin(arr, axis=None)：返回最小值所在位置的索引。
- ndarray.argmax(axis=None), np.argmax(arr, axis=None)：返回最大值所在位置的索引。
- np.argwhere(condition)：返回满足条件的所有元素的索引（与 np.where(condition) 类似，但返回的格式是 (N, ndim) 的数组）。
相关性与协方差：
- np.cov(m, y=None, rowvar=True)：计算协方差矩阵。
  - m：一个一维或二维数组。
  - rowvar=True (默认)：每行代表一个变量，每列代表一个观测。
  - rowvar=False：每列代表一个变量，每行代表一个观测。
- np.corrcoef(x, y=None, rowvar=True)：计算皮尔逊相关系数矩阵。

NumPy 的数学和统计函数同样受益于底层的 C 语言实现和矢量化。

高效聚合： 对于 sum, mean, min, max 等聚合操作，NumPy 会在 C 语言层面高效地遍历数组元素，执行累加、比较等操作，避免了 Python 循环的性能瓶颈。

axis 的作用： 当指定 axis 参数时，NumPy 会沿着该轴进行迭代，并在每个“切片”上执行聚合操作。例如，axis=0 意味着它会遍历所有列，对每列的所有行元素进行计算。

argmin/argmax： 这些函数通过遍历数组并跟踪当前最小值/最大值及其索引来实现。对于多维数组，它们会返回展平后的索引，或者在指定 axis 时返回沿着该轴的索引。

协方差和相关系数： 这些函数涉及更复杂的统计计算，包括均值、方差和元素乘积的求和。NumPy 在底层实现了这些数学公式，以高效地计算矩阵。协方差衡量两个变量共同变化的程度，相关系数是协方差的标准化版本，衡量两个变量线性关系的强度和方向。

(1)聚合函数

arr = np.array([1, 7, 2, 19, 23, 0, 88, 11, 6, 11])
np.min(arr)   # 0
np.max(arr)   # 88
np.sum(arr) # 168
np.mean(arr)  # 16.8
np.std(arr)  # 24.78628653106391
np.median(arr)  # 9.0  注意：不是ndarray的方法

(2)位置函数

arr
"""
array([ 1,  7,  2, 19, 23,  0, 88, 11,  6, 11])
"""
np.argmin(arr)  # 5
np.argmax(arr)  # 6

查找满足条件的位置索引：

arr
"""
array([ 1,  7,  2, 19, 23,  0, 88, 11,  6, 11])
"""
gt_20_index = np.argwhere(arr > 20)
gt_20_index
"""
array([[4],
       [6]])
"""
# 需要展平
gt_20_index_flattern = gt_20_index.flatten()
gt_20_index_flattern
"""
array([4, 6])
"""
# 取出这些元素：
gt_20 = arr[gt_20_index_flattern]
gt_20
"""
array([23, 88])
"""

(3)累积函数

arr
"""
array([ 1,  7,  2, 19, 23,  0, 88, 11,  6, 11])
"""
# 累积和
np.cumsum(arr)
"""
array([  1,   8,  10,  29,  52,  52, 140, 151, 157, 168])
"""
np.cumprod(arr)
"""
array([   1,    7,   14,  266, 6118,    0,    0,    0,    0,    0])
"""

(4)多维数组的聚合和位置函数

arr2 = np.random.randint(0, 10, (4, 5))
print(arr2)
"""
[[8 7 6 8 3]
 [1 7 4 4 7]
 [5 3 3 6 8]
 [5 6 0 3 2]]
"""
# 列的均值
col_mean = np.mean(arr2, axis = 0)
print(col_mean)
"""
[4.75 5.75 3.25 5.25 5.  ]
"""
# 行的均值
row_mean = np.mean(arr2, axis = 1)
print(row_mean)
"""
[6.4 4.6 5.  3.2]
"""
# 每列最大值索引
col_argmax = np.argmax(arr2, axis = 0)
print(col_argmax)
"""
[0 0 0 0 2]
"""
# 每行最小值索引
row_argmin = np.argmin(arr2, axis = 1)
print(row_argmin)
"""
[4 0 1 2]
"""

(5)协方差和相关系数

在机器学习和统计学中，协方差（Covariance）是一个核心概念，用于衡量两个随机变量之间线性关系的强度和方向。理解协方差对于数据分析、特征工程、降维（如主成分分析 PCA）以及各种统计建模都至关重要。

协方差衡量的是两个变量在相同方向上变化的程度。

如果两个变量倾向于同时增加或同时减少，则它们的协方差为正。
如果一个变量增加而另一个变量减少，则它们的协方差为负。
如果两个变量之间没有明显的线性关系，则它们的协方差接近于零。

协方差是对于方差的推广，对于两个随机变量，它们的协方差是反应它们两个之间的线性相关程度的，把 \(x_2\)换成\(x_1\) 那就是方差了，展开之后就是 \(x_1\)和 \(x_2\)的期望减去它们期望的乘积。

对于 n 维的向量 X，它的协方差就构成了一个协方差矩阵，第一行第一个是 \(x_1\) 和 \(x_1\) 的协方差（即 \(x_1\) 自身方差），第一行第二个是\(x_1\)和 \(x_2\)的协方差，第一行第 n 个是 \(x_1\)和 \(x_n\)的协方差。

显然这是一个对称阵，这在我们机器学习里面会经常使用的！

np.set_printoptions(suppress=True)
X = np.random.randint(1,20,size = (5,5)) 
print(X,X[:, 0], (np.mean(X[:, 0]**2) - (np.mean(X[:,0])**2)))  # 计算第1列的方差
display(np.cov(X,rowvar=False,bias = True))

print('第一行第一个协方差（第一列的方差）：%0.2f'%(np.mean(X[:,0]**2) - (np.mean(X[:,0]))**2)) 
# 计算第一个自己的方差：
print('第一行第二个协方差（第一列和第二列的协方差）：%0.2f'%(np.mean(X[:,0] * X[:,1])- X[:,0].mean()*X[:,1].mean()))
print('第一行最后一个协方差（第一列和最后一列协方差）：%0.2f'%(np.mean(X[:,0]*X[:,-1]) - (np.mean(X[:,0]))*(np.mean(X[:,-1])))) 

运行输出：

[[ 7  3  9 19 19]
 [14 17  4  8  1]
 [13 11  1 10  1]
 [ 1 13  3  6 10]
 [10  1 10  5 12]] [ 7 14 13  1 10] 22.0
array([[ 22.  ,   4.  ,  -1.6 ,  -0.2 , -19.4 ],
       [  4.  ,  36.8 , -17.6 ,  -9.2 , -32.  ],
       [ -1.6 , -17.6 ,  12.24,   4.36,  18.76],
       [ -0.2 ,  -9.2 ,   4.36,  25.04,  17.24],
       [-19.4 , -32.  ,  18.76,  17.24,  47.44]])
第一行第一个协方差（第一列的方差）：22.00
第一行第二个协方差（第一列和第二列的协方差）：4.00
第一行最后一个协方差（第一列和最后一列协方差）：-19.40

注意：上面计算的是总体方差（除以n），而不是样本方差（除以n-1）

# 3个变量和5个观测
data_for_cov = np.array([
    [1, 2, 3, 4, 5],
    [5, 4, 3, 2, 1],
    [10, 8, 6, 4, 2]
])
print(data_for_cov)
# rowvar=True 代表一行是一个变量
# bias=True有偏估计  除以n  bias=False 无偏估计，除以n-1
cov_matrix = np.cov(data_for_cov, rowvar=True, bias=True)  
print(cov_matrix)
"""
[[ 2. -2. -4.]
 [-2.  2.  4.]
 [-4.  4.  8.]]
"""
# 验证
print("第一行和第一行的协方差，即第一行的方差：")
ele0_0 = np.mean(data_for_cov[0]**2) - np.mean(data_for_cov[0])**2
print(ele0_0)
"""
2.0
"""
print("第一行和第二行的协方差：")
ele0_1 = np.mean(data_for_cov[0]*data_for_cov[1]) - np.mean(data_for_cov[0])*np.mean(data_for_cov[1])
print(ele0_1)
"""
-2.0
"""
print("第一行和第三行的协方差：")
ele0_1 = np.mean(data_for_cov[0]*data_for_cov[2]) - np.mean(data_for_cov[0])*np.mean(data_for_cov[2])
print(ele0_1)
"""
-4.0
"""

皮尔逊相关系数：

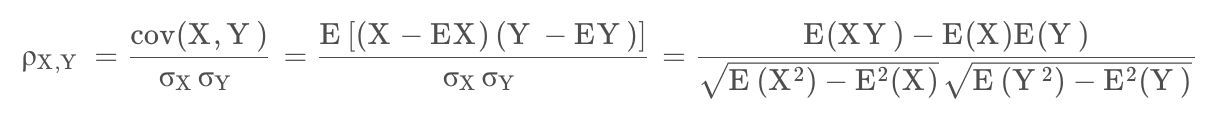
cov为协方差，\(\sigma\)为标准差。

print("原矩阵：")
"""
[[ 1  2  3  4  5]
 [ 5  4  3  2  1]
 [10  8  6  4  2]]
"""
print(data_for_cov)
# rowvar=True  每行是一个变量
correlation_matrix = np.corrcoef(data_for_cov, rowvar=True)
print('相关系数矩阵：')
print(correlation_matrix)
"""
[[ 1. -1. -1.]
 [-1.  1.  1.]
 [-1.  1.  1.]]
"""
# bais参数控制计算时除以n-1还是n, True表示除以n，False表示除以n-1；
cov_0_1 = np.cov(data_for_cov[0], data_for_cov[1], bias=True)
sigma0 = np.std(data_for_cov[0])
sigma1 = np.std(data_for_cov[1])
ele_0_1 = cov_0_1/(sigma0*sigma1)
ele_0_1
"""
array([[ 1., -1.],
       [-1.,  1.]])
"""

(6)选择题

给定 arr = np.array([[1, 2, 3], [4, 5, 6]])，执行 arr.sum(axis=0) 的结果是什么？

A. array([1, 2, 3, 4, 5, 6]) B. array([ 5, 7, 9]) C. array([ 6, 15]) D. array([21])

答案：B
以下哪个函数用于计算数组中最大值的索引？ A. np.max() B. np.min() C. np.argmax() D. np.argwhere()

答案：C

(7)编程题

创建一个 5*5 的 NumPy 数组 sales_data，包含 100 到 500 的随机整数，表示不同产品的销售额。
计算以下统计量并打印结果：
- 整个数组的平均销售额。
- 每种产品（行）的最高销售额。
- 每天（列）的最低销售额。
- 每种产品（行）的销售额累积和。
- 整个数组中销售额大于 300 的所有元素的索引。
创建一个包含两个变量（例如，广告投入和销售额）的 2*10 数组。计算并打印这两个变量之间的相关系数矩阵。

sales_data = np.random.randint(100, 501, size=(5, 5))
print(sales_data)
"""
[[102 311 254 259 237]
 [423 491 126 128 346]
 [203 178 273 121 432]
 [308 210 187 459 323]
 [137 288 231 412 350]]
"""
avg_all = np.mean(sales_data)
print(avg_all)
"""
271.56
"""
# 行最大值
row_max = np.max(sales_data, axis = 1)
print(row_max)
"""
[311 491 432 459 412]
"""
# 列最小值
col_min = np.min(sales_data, axis = 0)
print(col_min)
"""
[102 178 126 121 237]
"""
# 行累积和
cumsum_row = np.cumsum(sales_data, axis = 1)
print(cumsum_row)
"""
[[ 102  413  667  926 1163]
 [ 423  914 1040 1168 1514]
 [ 203  381  654  775 1207]
 [ 308  518  705 1164 1487]
 [ 137  425  656 1068 1418]]
"""
gt_300_index = np.argwhere(sales_data > 300)
print(gt_300_index)
"""
[[0 1]
 [1 0]
 [1 1]
 [1 4]
 [2 4]
 [3 0]
 [3 3]
 [3 4]
 [4 3]
 [4 4]]
"""
adv = np.random.randint(100, 201, (2, 10))
sal = np.random.randint(100, 501, (2, 10))
m = np.corrcoef(adv, sal)
m
"""
array([[ 1.        ,  0.09607699,  0.43863326, -0.07570837],
       [ 0.09607699,  1.        ,  0.38457674,  0.60552362],
       [ 0.43863326,  0.38457674,  1.        ,  0.22123934],
       [-0.07570837,  0.60552362,  0.22123934,  1.        ]])
"""

numpy-通用函数