python基础

python基础-元组tuple和集合set

Python元组是不可变、有序序列，可用小括号或tuple()创建，适合作为字典键。集合是无序、可变、无重复元素的序列，基于哈希表实现，支持高效增删查及集合运算。元组无生成式，集合可用生成式快速创建。

Posted by Hilda on June 30, 2025

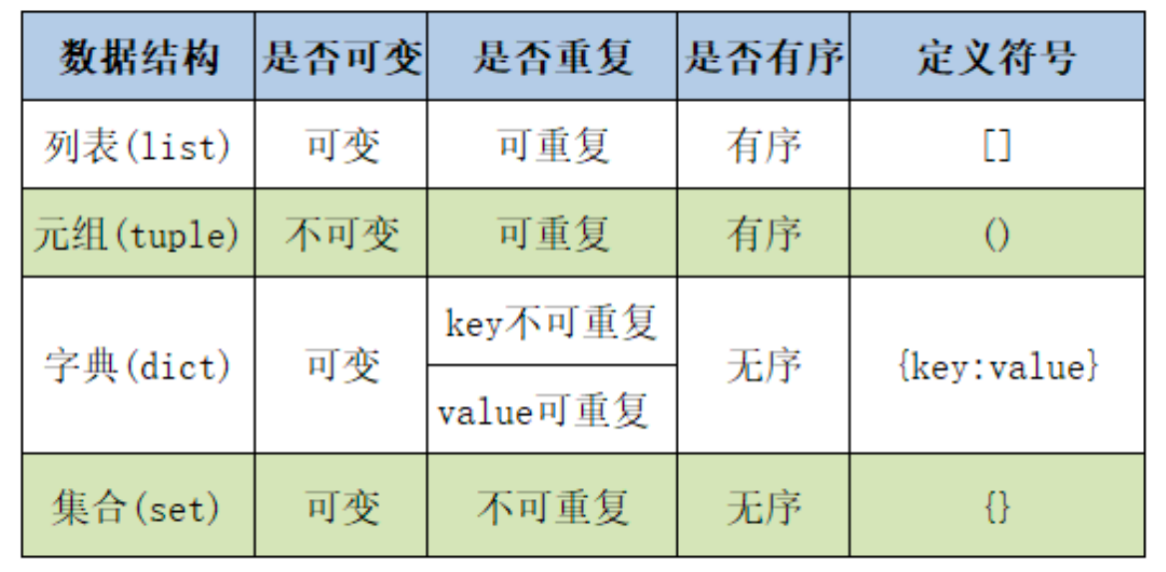
image-20250630150717828

注意没有元组生成式，其他结构都有相应的生成式。

1、什么是元组

元组是python的一个内置的数据结构，是一个不可变且有序序列。

这意味着一旦元组被创建，其中的元素就不能被修改、添加或删除。元组可以包含任意类型的数据，并且允许存在重复的元素。

不可变序列与可变序列

  • 不变可变序:字符串、元组，没有增、删，改的操作
  • 可变序列:列表、字典，可以对序列执行增、删、改操作，对象地址不发生更改

元组的不可变性是其核心特性。在Python内部，元组在创建时会分配一块固定大小的内存空间来存储其元素。由于元素在内存中的位置和值是固定的，因此无法进行修改。这种不可变性使得元组在某些场景下比列表更安全，例如作为字典的键（因为字典的键必须是不可变的），或者在函数中作为不可修改的数据传递，以防止意外的副作用。由于其固定结构，元组的访问速度通常比列表稍快。

例子：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

# 一个包含不同数据类型的元组
t1 = tuple((1, 2, 33.9, "Hello"))
print(t1, type(t1))
# 元组是有序的，可以通过索引访问元素
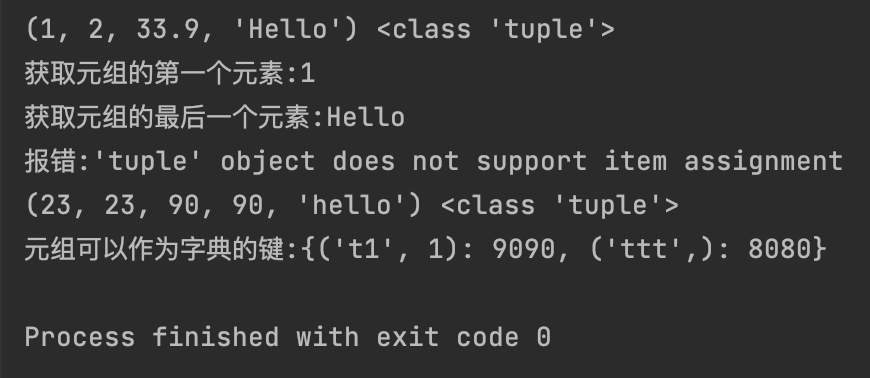
print(f"获取元组的第一个元素:{t1[0]}")
print(f"获取元组的最后一个元素:{t1[-1]}")
# 尝试修改元组中的元素会导致错误 (TypeError)
try:
    t1[0] = 90
except TypeError as e:
    print(f"报错:{e}") # 报错:'tuple' object does not support item assignment
# 元组允许重复元素
t2 = (23, 23, 90, 90, "hello")
print(t2, type(t2))
# 元组可以作为字典的键 (因为它是不可变的)
dict1 = {("t1", 1): 9090, ("ttt",): 8080}
print(f"元组可以作为字典的键:{dict1}")

image-20250629213441999

2、元组的创建方式

元组的创建方式非常灵活，主要通过使用小括号 () 或不使用小括号（隐式创建）来定义。特殊情况是创建只包含一个元素的元组，需要注意逗号 (,) 的使用。

以下是创建元组的主要方法：

  1. 使用小括号 ()
    • 空元组： empty_tuple = ()
    • 单个元素的元组： single_tuple = (1,) (注意： 必须有逗号)
    • 多个元素的元组： multi_ele_tuple = (1, 2, "hello")
  2. 隐式创建 (元组打包)
    • 当多个值用逗号分隔时，它们会自动打包成一个元组。
    • implicit_tuple = "World", 23, 90
  3. 使用 tuple() 构造函数
    • 空元组： empty_tuple2 = tuple()
    • 从可迭代对象创建： 将列表、字符串、或其他元组转换为新元组。
      • 从列表：list2tuple = tuple([1, 3.3, "你好"])
      • 从字符串：str2tuple = tuple('今天也是卷') (每个字符成为一个元素)
      • 从现有元组：t_to = tuple(t_orig) (创建副本)，引用是一样的

例子：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

# 创建空元组
empty_tuple = ()
empty_tuple2 = tuple()
print(empty_tuple, type(empty_tuple), empty_tuple2, type(empty_tuple2))

# 创建只包含一个元素的元组 (注意逗号的重要性)
single_tuple = (1,)
print(single_tuple, type(single_tuple))
try:
    single_tuple2 = tuple(2, )
except TypeError as e:
    print(f"报错：{e}")  # 报错：'int' object is not iterable

not_tuple = (3)
print(not_tuple, type(not_tuple))  # 3 <class 'int'>

# 创建包含多个元素的元组
multi_ele_tuple = (1, 2, 99.9, "SEU")
print(f"元组是：{multi_ele_tuple}, 第一个元素是：{multi_ele_tuple[0]}")

# 隐式创建元组 (省略括号) - 称为元组打包 (tuple packing)
implicit_tuple = "World", 23, 90, 9
print(implicit_tuple, type(implicit_tuple))

# 使用 tuple() 构造函数从可迭代对象创建元组
# 从列表创建
list2tuple = tuple([1, 3.3, "你好"])
print(list2tuple, type(list2tuple))
# 从字符串创建 (每个字符成为一个元素)
str2tuple  = tuple('今天也是卷')
print(str2tuple, type(str2tuple))
# 从另一个元组创建 (会创建一个副本), 应用是一样的
t_orig = 90.8, 9090, "卷王就是我"
t_to = tuple(t_orig)
print(f"原先的元组:{t_orig}, id是{id(t_orig)}, 由此创建的元组:{t_to}, id是{id(t_to)}")

3、元组的遍历

由于元组是有序的，我们可以像遍历列表一样遍历元组中的元素。最常见的方法是使用 for 循环，也可以结合 enumerate() 函数同时获取索引和值。

【1】使用 for in循环遍历元组元素

1
2
3

my_tuple = ("apple", "banana", "cherry", "date")
for item in my_tuple:
    print(item, end="\t")

【2】使用 for 循环和 range() 通过索引遍历元组

1
2

for i in range(len(my_tuple)):
    print(f"第{i}个元素是{my_tuple[i]}", end=" ")

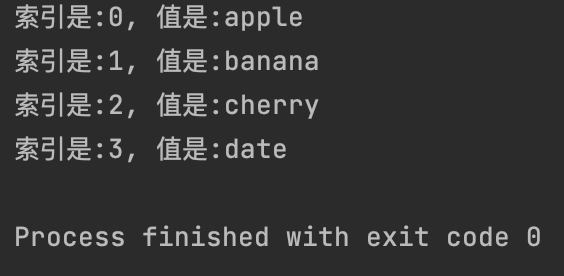
【3】使用 for 循环和 enumerate() 遍历元组 (推荐)

1
2

for index, value in enumerate(my_tuple):
    print(f"索引是:{index}, 值是:{value}")

image-20250630111519807

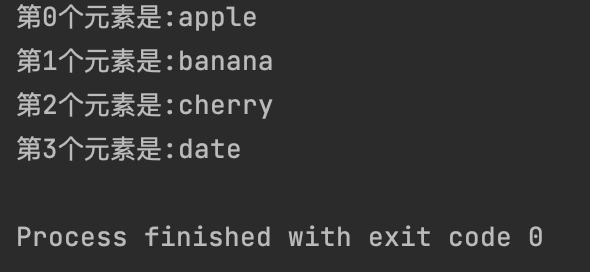
【4】使用 while 循环通过索引遍历元组

1
2
3
4

i = 0
while i < len(my_tuple):
    print(f"第{i}个元素是:{my_tuple[i]}")
    i += 1

image-20250630111644423

4、什么是集合

image-20250630145604213

集合（Set）是Python中一种无序（unordered）、可变（mutable）的序列类型，其核心特点是不允许重复元素（no duplicate elements）。集合的这些特性使其非常适合用于执行数学中的集合运算，例如求并集、交集、差集等。

Python的集合是基于哈希表（hash table）实现的。这意味着集合中的每个元素都必须是可哈希的（hashable），即不可变的对象（如数字、字符串、元组）。当一个元素被添加到集合中时，Python会计算其哈希值并将其存储在哈希表中。由于哈希表的特性，查找、添加和删除元素的平均时间复杂度为 O(1)，效率非常高。同时，哈希表也保证了元素的唯一性，因为每个哈希值只对应一个存储位置。

【1】创建一个集合,输出类型

1
2

my_set = {1, 2, 3, 4, "Hello"}
print(my_set, type(my_set))

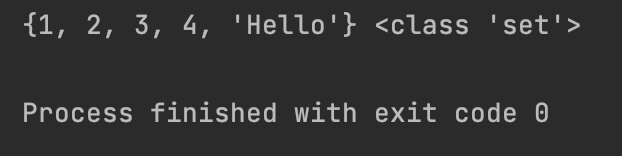
image-20250630111856282

【2】集合是无序的，所以每次打印顺序可能不同；尝试添加重复元素，集合会自动处理，不会报错，也不会添加

1
2
3

my_set.add(3)
my_set.add(4)
print(my_set)

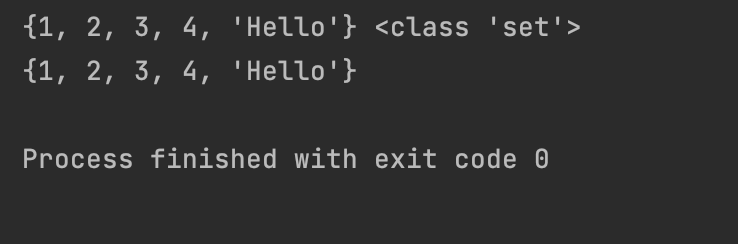
image-20250630112007782

【3】集合中的元素必须是可哈希的 (不可变的)；列表是不可哈希的，所以不能作为集合的元素

1
2
3
4

try:
    invalid_set = {[1, 2], 3}
except TypeError as e:
    print(f"报错：{e}")

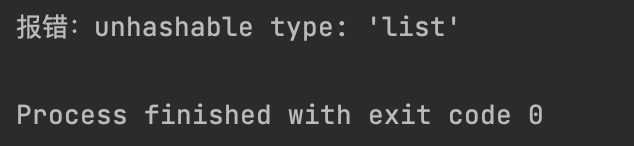
image-20250630112125291

【4】元组是可哈希的，可以作为集合的元素

1
2

set_with_tuple = {(1, 2), (3, 4), 8, "Hello World"}
print(set_with_tuple)

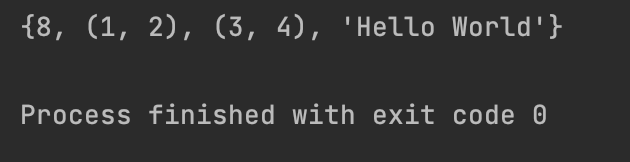
image-20250630112230381

可以看到8先打印了，也证明了set是无序的。

5、集合的创建

创建集合有两种主要方式：使用大括号 {} 和使用 set() 构造函数。需要特别注意的是，使用 {} 创建空集合时，它会被认为是字典，而创建空集合必须使用 set()。

【1】使用 {} 创建包含元素的集合。注意：如果 {} 中没有元素，它会创建一个空字典，而不是空集合

1
2

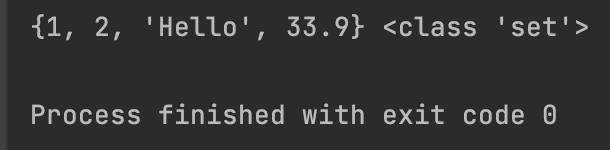
set1 = {1, 2, 33.9, "Hello"}
print(set1, type(set1))

image-20250630140950861

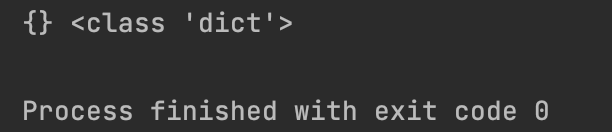
特别注意：{} 创建的是空字典，不是空集合

1
2

d = {}
print(d, type(d))

image-20250630141134476

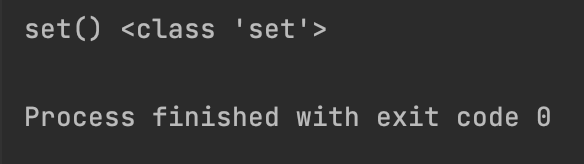
【2】使用 set() 构造函数创建空集合 (重要!)

1
2

empty_set1 = set()
print(empty_set1, type(empty_set1))

image-20250630141046151

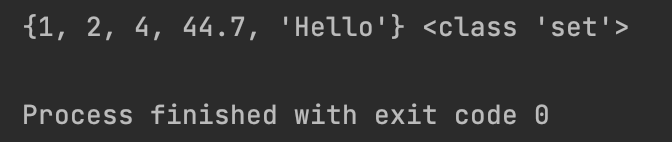
【3】使用 set() 构造函数从可迭代对象创建集合,注意到：重复元素会被删除

1
2

set_from_list = set([1, 2, 2, 4, 4, 44.7, "Hello"])
print(set_from_list, type(set_from_list))

image-20250630141305239

从字符串创建 (每个字符成为一个元素，且顺序不保证，重复字符会被删除)

1
2

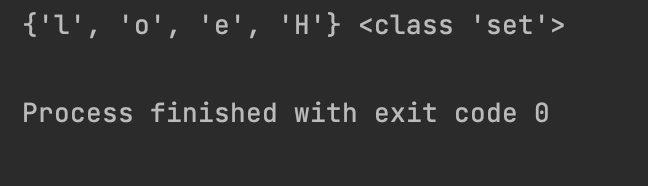
set_from_str = set("Hello")
print(set_from_str, type(set_from_str))

image-20250630141404513

从元组创建：

1
2

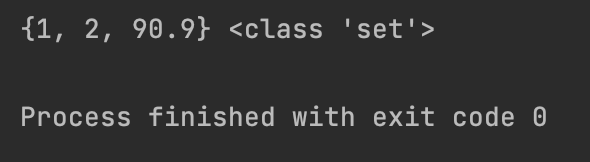
set_from_tuple = set((1, 2, 2, 90.90, 90.90))
print(set_from_tuple, type(set_from_tuple))

image-20250630141457285

6、集合的增、删、改、查操作

集合作为可变数据类型，支持元素的添加和删除。由于其无序性和唯一性，集合没有“修改”某个特定元素的概念，修改通常意味着先删除旧元素再添加新元素。集合还支持丰富的集合运算（如并集、交集等）和成员检测。

（1）添加元素

【1】添加元素add()，如果是重复元素，不会重复添加，也不会报错：

1
2
3
4
5
6
7

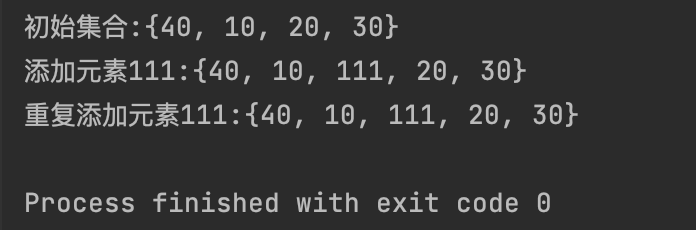
my_set = {10, 20, 30, 40}
print(f"初始集合:{my_set}")

my_set.add(111)
print(f"添加元素111:{my_set}")
my_set.add(111)
print(f"重复添加元素111:{my_set}")

image-20250630141736954

【2】update(): 添加多个元素 (参数可以是列表、元组、其他集合等可迭代对象)

注意下面代码中的细节：

1
2
3
4
5
6
7
8
9
10

my_set.update([30, 40, 50, 60, 70]) # 重复添加元素30，40
print(my_set)
my_set.update((90, 80, 222))
print(my_set)
my_set.update({999, 888})
print(my_set)
my_set.update("Hello")
print(my_set)
my_set.update(["Hello"])
print(my_set)

image-20250630142045088

（2）删除元素

【1】remove(element): 删除指定元素。如果元素不存在，会报错 KeyError

1
2
3
4
5
6
7

print(f"现在的集合:{my_set}")
my_set.remove(999)
print(f"删除999的集合:{my_set}")
try:
    my_set.remove("m")
except KeyError as e:
    print(f"报错:{e}")

image-20250630142346268

【2】discard(element): 删除指定元素。如果元素不存在，不会报错

1
2
3
4
5

print(f"现在的集合:{my_set}")
my_set.discard(90)
print(f"删除90的集合:{my_set}")
my_set.discard(999999999)
print(f"尝试删除不存在的元素也不会报错:{my_set}")

image-20250630142531005

【3】pop(): 随机删除并返回一个元素。集合是无序的，所以不知道哪个元素会被删除。空集合调用会报错 KeyError。

1
2
3
4
5
6
7
8

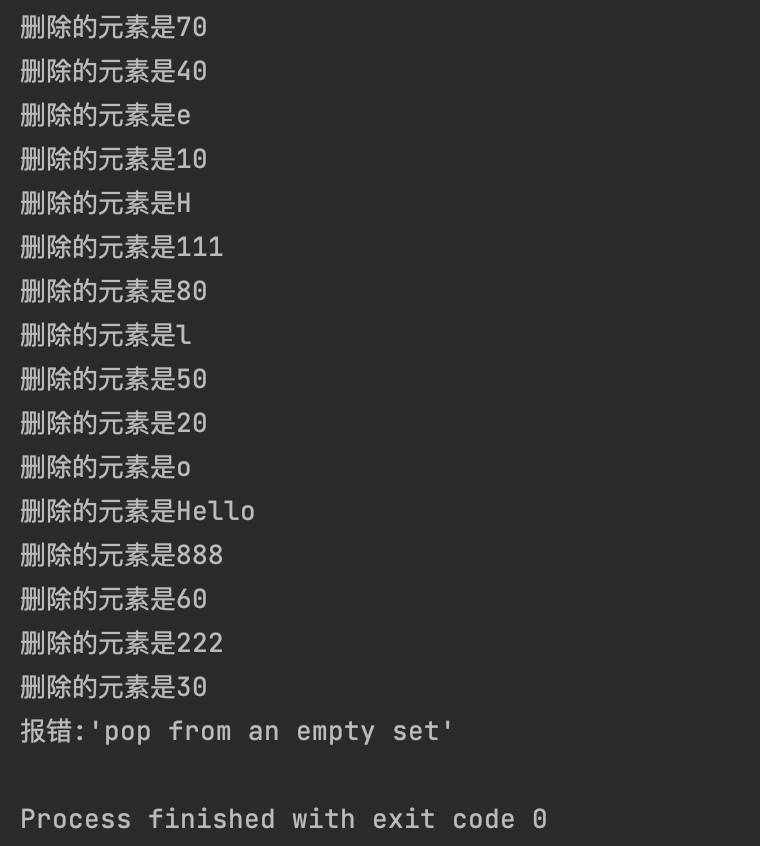
while my_set:
    i = my_set.pop()
    print(f"删除的元素是{i}")
# 此时my_set是空集合了
try:
    my_set.pop()
except KeyError as e:
    print(f"报错:{e}")

image-20250630142758995

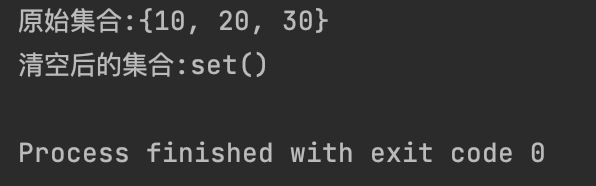
【4】clear(): 清空集合中的所有元素

1
2
3
4

my_set = {10, 20, 30}
print(f'原始集合:{my_set}')
my_set.clear()
print(f'清空后的集合:{my_set}')

image-20250630142913791

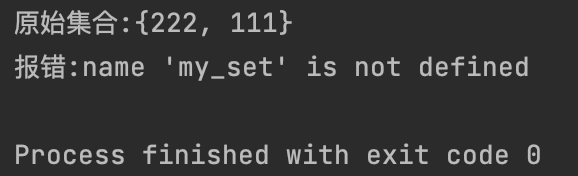
【5】del:删除引用

1
2
3
4
5
6
7

my_set = {111, 222, 222}
print(f"原始集合:{my_set}")
del my_set
try:
    print(f"删除引用后:{my_set}")
except NameError as e:
    print(f"报错:{e}")

image-20250630143110547

（3）修改元素

集合元素本身是不可变的。对集合的“修改”通常指增删元素。

（4）查询元素

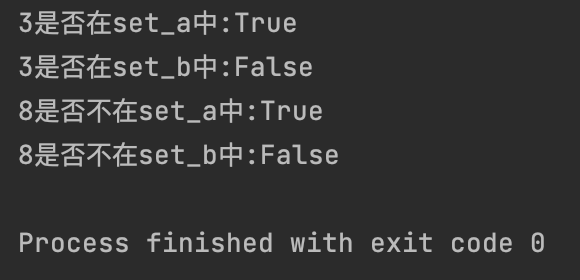
【1】成员检测：in、not in操作符

1
2
3
4
5
6
7

set_a = {1, 2, 3, 4, 5}
set_b = {4, 5, 6, 7, 8}

print(f"3是否在set_a中:{3 in set_a}")
print(f"3是否在set_b中:{3 in set_b}")
print(f"8是否不在set_a中:{8 not in set_a}")
print(f"8是否不在set_b中:{8 not in set_b}")

image-20250630143400327

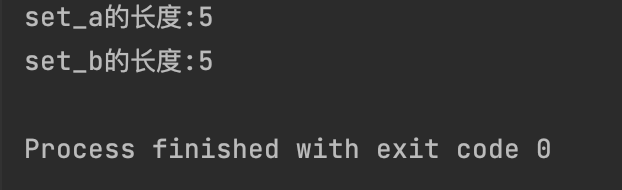
【2】 长度 (len() 函数)

1
2

print(f"set_a的长度:{len(set_a)}")
print(f"set_b的长度:{len(set_b)}")

image-20250630143447358

（5）集合运算

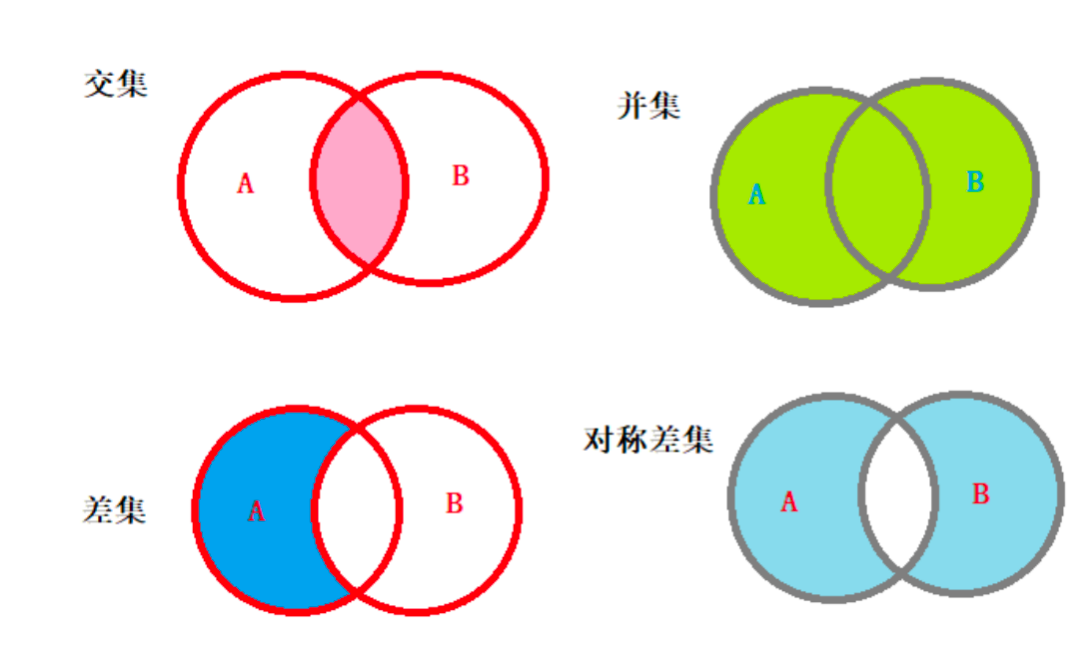
image-20250630150647196

【1】并集 (Union): 所有元素的集合 union与|是等价的

1
2
3
4

union_set = set_a.union(set_b)
print(f"集合A:{set_a}")
print(f"集合B:{set_b}")
print(f"求合集:{union_set}")

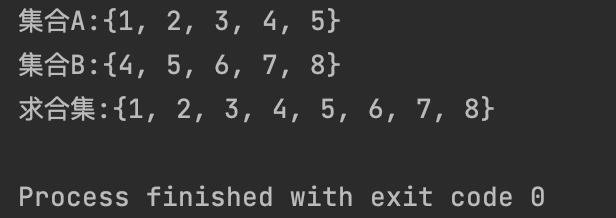
image-20250630144035425

【2】交集 (Intersection): 共同元素的集合 注意：Intersection与&是等价的

1
2

intersect = set_a.intersection((set_b))
print(f"求交集:{intersect}")

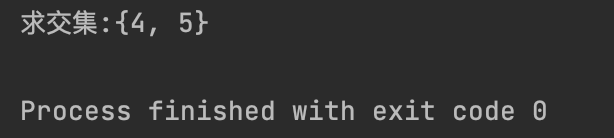
image-20250630144126223

【3】差集 (Difference): 属于A但不属于B的元素 Difference与-(减号)是等价的

1
2

diff = set_a.difference(set_b)
print(f"求差集:{diff}")

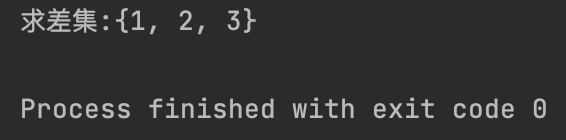
image-20250630144218925

【4】对称差集 (Symmetric Difference): 属于A或属于B，但不属于两者的共同部分 与^（位运算中的异或）等价

1
2

diff_all = set_a.symmetric_difference(set_b)
print(f"对称差集:{diff_all}")

image-20250630144322470

【5】两个集合是否相等：可以使用运算符==或!=进行判断

1
2
3
4
5

sA = {1, 2, 3}
sB = {1, 2, 3}
sC = {1, 2, 4}
print(sA == sB)
print(sA == sC)

image-20250630150501794

【6】两个集合是否没有交集 ：可以调用方法isdisjoint进行判断

1
2
3

print(f"集合A和集合B是否没有交集:{sA.isdisjoint(sB)}")
sD = {5, 6, 7}
print(f"集合A和集合D是否没有交集:{sA.isdisjoint(sD)}")

image-20250630150620536

（6）子集与超集

1
2
3
4
5
6

set_c = {1, 2}
set_d = {1, 2, 3}
print(f"集合C:{set_c}, 集合D:{set_d}")
print(f"集合C是集合D的子集吗？{set_c.issubset(set_d)}")
print(f"集合C是集合D的超集吗？{set_c.issuperset(set_d)}")
print(f"集合D是集合C的超集吗？{set_d.issuperset(set_c)}")

image-20250630144544987

7、集合生成式

集合生成式（Set Comprehension）是一种简洁的语法，用于从现有可迭代对象（如列表、元组、字符串等）快速创建新的集合。它的语法与列表生成式类似，但使用大括号 {}。这使得代码更具可读性和效率。

集合生成式在内部高效地迭代输入的可迭代对象，对每个元素应用一个表达式，并根据需要添加一个可选的条件。由于集合的去重特性，任何通过生成式计算出的重复值都只会在最终集合中出现一次。这在需要快速生成一个去重集合的场景中非常有用。

【1】基本集合生成式：从列表中创建平方数的集合

1
2
3

numbers = [1, 2, 3, 4, 5, 1, 2]
s1 = {i**2 for i in numbers}
print(f"从列表 {numbers} 生成的平方数集合:{s1}")

image-20250630144803804

【2】带有条件的集合生成式：

1
2

s2 = {i for i in numbers if i % 2 == 0}
print(f"从列表中创建偶数的集合:{s2}")

image-20250630144910908

【3】从字符串中提取非重复字符的集合

1
2
3

str_ = "Hello World"
s3 = {i for i in str_ if i != " "}
print(f"从字符串 '{str_}' 提取的唯一字符集合: {s3}")

image-20250630145040513

【4】嵌套的集合生成式 (不常见，但可行)

1
2
3

nested_list = [[1, 2], [3, 4, 1], [5]]
s4 = {item for sublist in nested_list for item in sublist}
print(f"从嵌套列表生成的扁平化集合:{s4}")

image-20250630145210175

【5】使用函数在生成式中处理元素

1
2
3
4
5
6
7
8
9
10
11

def is_prime(n):
    if n < 2:
        return False
    for i in range(2, (int)(n ** 0.5) + 1):
        if n % i == 0:
            return False
    return True

nums_for_prime = range(1, 11)
prime_numbers_set = {n for n in nums_for_prime if is_prime(n)}
print(f"从范围 {list(nums_for_prime)} 生成的质数集合: {prime_numbers_set}")

image-20250630145441541

CATALOG
    FEATURED TAGS
    书籍阅读 算法 人工智能AI基础 python基础 机器学习-吴恩达 力扣 spring6 Java基础 numpy ollama工具 pandas
    FRIENDS